整数划分问题是算法中的一个经典命题之一,有关这个问题的讲述在讲解到递归时基本都将涉及。所谓整数划分,是指把一个正整数n写成如下形式:
n=m1+m2+...+mi; (其中mi为正整数,并且1 <= mi <= n),则{m1,m2,...,mi}为n的一个划分。
如果{m1,m2,...,mi}中的最大值不超过m,即max(m1,m2,...,mi)<=m,则称它属于n的一个m划分。这里我们记n的m划分的个数为f(n,m);
例如但n=4时,他有5个划分,{4},{3,1},{2,2},{2,1,1},{1,1,1,1};
注意4=1+3 和 4=3+1被认为是同一个划分。
该问题是求出n的所有划分个数,即f(n, n)。下面我们考虑求f(n,m)的方法;
---------------------------------------------------------------------
(一)递归法
---------------------------------------------------------------------
根据n和m的关系,考虑以下几种情况:
(1)当n=1时,不论m的值为多少(m>0),只有一种划分即{1};
(2) 当m=1时,不论n的值为多少,只有一种划分即n个1,{1,1,1,...,1};
(3) 当n=m时,根据划分中是否包含n,可以分为两种情况:
(a). 划分中包含n的情况,只有一个即{n};
(b). 划分中不包含n的情况,这时划分中最大的数字也一定比n小,即n的所有(n-1)划分。
因此 f(n,n) =1 + f(n,n-1);
(4) 当n<m时,由于划分中不可能出现负数,因此就相当于f(n,n);
(5) 但n>m时,根据划分中是否包含最大值m,可以分为两种情况:
(a). 划分中包含m的情况,即{m, {x1,x2,...xi}}, 其中{x1,x2,... xi} 的和为n-m,可能再次出现m,因此是(n-m)的m划分,因此这种划分
个数为f(n-m, m);
(b). 划分中不包含m的情况,则划分中所有值都比m小,即n的(m-1)划分,个数为f(n,m-1);
因此 f(n, m) = f(n-m, m)+f(n,m-1);
综合以上情况,我们可以看出,上面的结论具有递归定义特征,其中(1)和(2)属于回归条件,(3)和(4)属于特殊情况,将会转换为情况(5)。而情况(5)为通用情况,属于递推的方法,其本质主要是通过减小m以达到回归条件,从而解决问题。其递推表达式如下:
f(n, m)= 1; (n=1 or m=1)
f(n, n); (n<m)
1+ f(n, m-1); (n=m)
f(n-m,m)+f(n,m-1); (n>m)
因此我们可以给出求出f(n, m)的递归函数代码如下(引用Copyright Ching-Kuang Shene July/23/1989的代码):
unsigned long GetPartitionCount(int n, int max)
{
if (n == 1 || max == 1)
return 1;
else if (n < max)
return compute(n, n);
else if (n == max)
return 1 + GetPartitionCount(n, max-1);
else
return GetPartitionCount(n,max-1) + GetPartitionCount(n-max, max);
}
我们可以发现,这个命题的特征和另一个递归命题:
“上台阶”问题(斐波那契数列)(http://www.cnblogs.com/hoodlum1980/archive/2007/07/13/817188.html)
相似,也就是说,由于树的“天然递归性”,使这类问题的解可以通过树来展现,每一个叶子节点的路径是一个解。因此把上面的函数改造一下,让所有划分装配到一个.NET类库中的TreeView控件,相关代码(c#)如下:
/// <param name="root">树的根结点</param>
/// <param name="n">被划分的整数</param>
/// <param name="max">一个划分中的最大数</param>
/// <returns>返回划分数,即叶子节点数</returns>
private int BuildPartitionTree(TreeNode root, int n, int max)
{
int count=0;
if( n==1)
{
//{n}即1个n
root.Nodes.Add(n.ToString());//{n}
return 1;
}
else if( max==1)
{
//{1,1,1,
 ,1} 即n个1
,1} 即n个1TreeNode lastNode=root;
for(int j=0;j<n;j++)
{
lastNode.Nodes.Add("1");
lastNode=lastNode.LastNode;
}
return 1;
}
else if(n<max)
{
return BuildPartitionTree(root, n, n);
}
else if(n==max)
{
root.Nodes.Add(n.ToString()); //{n}
count=BuildPartitionTree(root, n, max-1);
return count+1;
}
else
{
//包含max的分割,{max, {n-max}}
TreeNode node=new TreeNode(max.ToString());
root.Nodes.Add(node);
count += BuildPartitionTree(node, n-max, max);
//不包含max的分割,即所有max-1分割
count += BuildPartitionTree(root, n, max-1);
return count;
}
}
如果我们要输出所有解,只需要输出所有叶子节点的路径即可,可以同样用递归函数来输出所有叶子节点(代码中使用了一个StringBuilder对象来接收所有叶子节点的路径):
private void PrintAllLeafPaths(TreeNode node)
{
//属于叶子节点?
if(node.Nodes.Count==0)
this.m_AllPartitions.AppendFormat("{0} ", node.FullPath.Replace('\',','));
else
{
foreach(TreeNode child in node.Nodes)
{
this.PrintAllLeafPaths(child);
}
}
}
这个小例子的运行效果如下(源代码都在文中,就不提供下载链接):
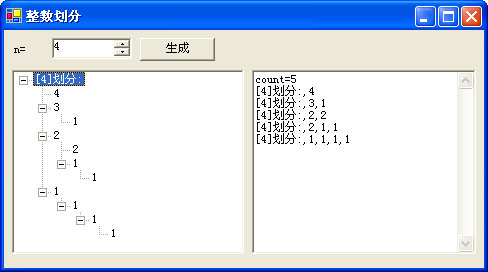
通过递归思路,我们给出了n的划分个数的算法,也把所有划分组装到一棵树中。好,关于递归思路我们就暂时介绍到这里。关于输出所有划分的标准代码在这里省略了,我们有时间再做详细分析。
---------------------------------------------------------------------
(二)母函数法
---------------------------------------------------------------------
下面我们从另一个角度即“母函数”的角度来考虑这个问题。
所谓母函数,即为关于x的一个多项式G(x):
有 G(x)= a0 + a1*x + a2*x^2 + a3*x^3 + ...
则我们称G(x)为序列(a0,a1,a2,...)的母函数。关于母函数的思路我们不做更多分析。
我们从整数划分考虑,假设n的某个划分中,1的出现个数记为a1,2的个数记为a2,..., i的个数记为ai,
显然: ak<=n/k; (0<= k <=n)
因此n的划分数f(n,n),也就是从1到n这n个数字中抽取这样的组合,每个数字理论上可以无限重复出现,即个数随意,使他们的总和为n。显然,数字i可以有如下可能,出现0次(即不出现),1次,2次,..., k次,等等。把数字i用(x^i)表示,出现k次的数字i用 x^(i*k)表示, 不出现用1表示。例如数字2用x^2表示,2个2用x^4表示,3个2用x^6表示,k个2用x^2k表示。
则对于从1到N的所有可能组合结果我们可以表示为:
G(x) = (1+x+x^2+x^3+...+x^n) (1+x^2+x^4+...) (1+x^3+x^6+...) ... (1+x^n)
= g(x,1) g(x,2) g(x,3) ... g(x, n)
= a0 + a1* x + a2* x^2 + ... + an* x^n + ... ; (展开式)
上面的表达式中,每一个括号内的多项式代表了数字i的参与到划分中的所有可能情况。因此该多项式展开后,由于x^a * x^b=x^(a+b),因此 x^i 就代表了i的划分,展开后(x^i)项的系数也就是i的所有划分的个数,即f(n,n)=an (上式中g(x,i)表示数字i的所有可能出现情况)。
由此我们找到了关于整数划分的母函数G(x);剩下的问题是,我们需要求出G(x)的展开后的所有系数。
为此我们首先要做多项式乘法,对于我们来说并不困难。我们把一个关于x的一元多项式用一个整数数组a[]表示,a[i]代表x^i的系数,即:
g(x) = a[0] + a[1]x + a[2]x^2 + ... + a[n]x^n;
则关于多项式乘法的代码如下,其中数组a和数组b表示两个要相乘的多项式,结果存储到数组c:
#define N 130
unsigned long a[N];/*多项式a的系数数组*/
unsigned long b[N];/*多项式b的系数数组*/
unsigned long c[N];/*存储多项式a*b的结果*/
/*两个多项式进行乘法,系数分别在a和b中,结果保存到c ,项最大次数到N */
/*注意这里我们只需要计算到前N项就够了。*/
void Poly()
{
int i,j;
memset(c,0,sizeof(c));
for(i=0; i<N; i++)
for(j=0; j<N-i; j++) /*y<N-i: 确保i+j不会越界*/
c[i+j] += a[i]*b[j];
}
下面我们求出G(x)的展开结果,G(x)是n个多项式连乘的结果:
/*计算出前N项系数!即g(x,1) g(x,2)... g(x,n)的展开结果*/
void Init()
{
int i,k;
memset(a,0,sizeof(a));
memset(c,0,sizeof(c));
for(i=0;i<N;i++) a[i]=1; /*第一个多项式:g(x, 1) = x^0 + x^1 + x^2 + x^3 +
 */
*/for(k=2;k<N;k++)
{
memset(b,0,sizeof(b));
for(i=0;i<N;i+=k) b[i]=1;/*第k个多项式:g(x, k) = x^0 + x^(k) + x^(2k) + x^(3k) +
 */
*/Poly(); /* 多项式乘法:c= a*b */
memcpy(a,c,sizeof(c)); /*把相乘的结果从c复制到a中:c=a; */
}
}
通过以上的代码,我们就计算出了G(x)的展开后的结果,保存到数组c中。此时有:f(n,n)=c[n];剩下的工作只是把相应的数组元素输出即可。
问题到了这里已经解决完毕。但我们发现,针对该问题,g(x,k)是一个比较特殊的多项式,特点是只有k的整数倍的索引位置有项,而其他位置都为0,具有项“稀疏”的特点,并且项次分布均匀(次数跨度为k)。这样我们就可以考虑在计算多项式乘法时,可以减少一些循环。因此可以对Poly函数做这样的一个改进,即把k作为参数传递给Poly:
/*两个多项式进行乘法,系数分别在a和b中,结果保存到c ,项最大次数到N */
/*改进后,多项式a乘以一个有特殊规律的多项式b,即b中只含有x^(k*i)项,i=0,1,2,
 */
*//*如果b没有规律,只需要把k设为1,即与原来函数等效*/
void Poly2(int k) /*参数k的含义:表示b中只有b[k*i]不为0!*/
{
int i,j;
memset(c,0,sizeof(c));
for(i=0; i<N; i++)
for(j=0; j<N-i; j+=k)
c[i+j] += a[i]*b[j];
}
这样,原有的函数可以认为是k=1的情况(即多项式b不具有上诉规律)。相应的,在上面的Init函数中的调用改为Poly2(k)即可。
---------------------------------------------------------------------------------
参考资料:
(1)关于“递归”部分的代码,参考了Ching-Kuang Shene,July/23/1989的代码;
(2)关于“母函数”部分,参考了《Acm程序设计》(刘春英)(PPT文档);
(3)“母函数”方法的Init和Poly的代码,参考了某位教师的代码 : ymc 2008/09/25, 其中多项式乘法的改进是我提出的建议。
-- by hoodlum1980 2008-10-11