-
前言
挖坑,开始填。--2020/04/30
填完啦。 -- 2021/02/07
这个网络流的大坑当时是疫情期间长寒假挖的,后来因为比较忙就写完增广路然后就没了。
本来是打算暑假写的,最后暑假要准备 CSP/NOIP2020 所以暑假和暑假后的时间都没有更新。
后来又碰上一检,原计划是复习期间更完,但是最后因为 whk 繁忙和上下界网络流还不熟悉的原因就放在了寒假。
所以我甚至快咕了一年。但最后还是完成了。或许以后会补充一些东西?
印象最深了是最大权闭合子图,那个证明看到凌晨 1 点然后为了珍贵的头发就只好先不看(什么什么头发最重要是吧是吧。
如果有不足的地方欢迎随时指出。顺便求个赞。好耶!
-
概念
网络流(network-flows)是一种类比水流的解决问题方法,与线性规划密切相关。 ---百度百科
主要用于解决流量问题。
首先,他是一个有向图。
并且满足下面 (3) 条性质:
仅有一个入度为 (0) 的点,叫做源点 (s) 。 其实就是流量的源头。
仅有一个出度为 (0) 的点,叫做汇点 (t) 。 就是所有流最后汇聚到的一个点。
每一条边权都非负,叫做边的容量 (c(u,v)) , 表示从 (u) 到 (v) 最多可以流过的量。
因为流的时候不可能每条都流满,所以设实际的流量为 (f(u,v)) 。
显然,(f(u,v) le c(u,v)) 。
可行流:满足 (0 le f(u,v) le c(u,v)) ,并且除去源点 (s) 和汇点 (t) 以外的点,都满足入度等于出度(边/点不会自己制造流量)。
举例子。下图就是一个可行流。
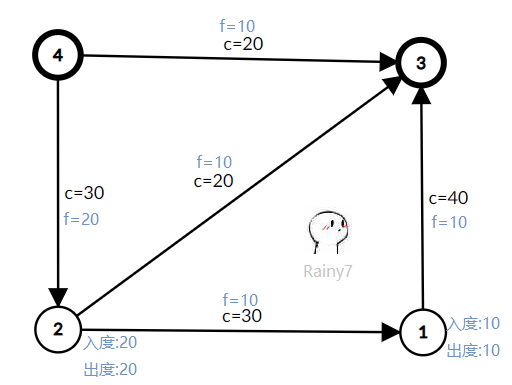
对于每条弧,还有如下的特殊情况。
饱和弧:(f(u,v)=c(u,v)) ,相对的,非饱和弧:(f(u,v)<c(u,v)) 。
零流弧:(f(u,v)=0) ,相对的,非零流弧:(f(u,v)>0) 。
当任意 (u,v in V) 都满足 (f(u,v)=0) , 则称这个网络流为零流。
如果一个网络流只满足 (f(u,v) le c(u,v)) ,但不满足入度等于出度的情况,称为伪流。
对于任意一种可行流,定义 (cl(u,v)=c(u,v)-f(u,v)) 是边 ((u,v)) 残留流量。
对于一种可行流,每条边都设一个 (cl(u,v)) , 且每条边都设置一个反向边,其容量为此次找到的流量,这样的图称为残余网络。
-
最大流 (增广路部分)
网络的最大流就是求源点流向汇点的最多流量,并且要满足是一个可行流。
如果给出一个残余网络,能在上面找到一条路从源点 (s) 到汇点 (t) , 满足上面每条边 (cl(u,v)>0) , 那么一定就可以沿着这个路来传送更多流量。
这就是增广路。
那可以通过找增广路来找最大流。
当然这非常不靠谱。如下图:
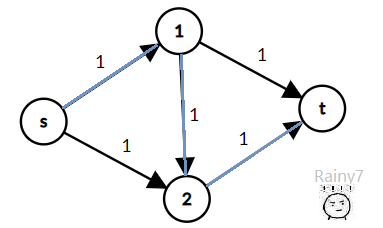
找到的路是 s-1-2-t ,流量为1。
但很显然有更好的方法,分成2条路: s-1-t 和 s-2-t ,流量为2。
那优化的方法,就是要反悔这条路。
但如果把每条路都dfs出来的话,就慢的离谱。
所以,建立反悔边,即反向边,边权就是 (f(u,v)) 。
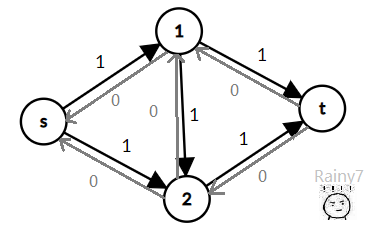
这样就相当于给了边一个反悔的机会。
上面那个图,第二次找增广路时,就会找到s-2-1-t这条路,这样流量又多了 (1) 。
那么结果正确,最大流为 (2) 。
这就是用增广路找最大流的方法了。
如果用dfs找增广路,那么就是FF算法。
慢的离谱。
作为优化,用bfs找增广路,是EK算法。
复杂度是 (O(VE^2)) 。
其实也很慢,那么接下来介绍的就是Dinic算法。
每次找增广路都要跑一次bfs,这实在太慢了啊。而Dinic算法其实本质就是让一次dfs求多个增广路。
首先,先把这个图分层,根据每个点到汇点的最短路不同来分为不同层。注意:这里最短路的边权均为1。

所以一条增广路,肯定是从第一层到最后一层中各有一个。
那么先跑dfs,找到第一条增广路。那么为了找到更多,我们应该适当回溯,然后再找一条。
那么如何回溯呢?
一次增广后,如果这条边容量 ((u,v)) 为 (0) , 说明此边用不着了,回溯。一直回溯到不满足后再增广。
那么如果回溯到源点,并且无路可走,那么此次 dfs 结束,也得到了一个新的残余网络。
注意:每次dfs前都要重新分层。
而且用原来的图减去最后的残余网络,就可以得到每条边的流量。
这样的复杂度就是 (O(V^2E)) 。
这个复杂度看上去还是有点高,但其实大多数情况都是跑不满的,
所以有一些大数据甚至跑的飞快。然后其实Dinic还可以再二分图上跑,
似乎比匈利亚快,复杂度是 (O( sqrt{V}E )) 。当然我更愿意写匈利亚毕竟匈利亚这么好写。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<queue>
using namespace std;
const int Maxn=1e4+5;
const int Maxm=3e5+5;
const int inf=1e9;
struct edge{
int v,w,nx;
}e[Maxm];
int n,m,sc,tc,ans,ne=-1,f[Maxn],deep[Maxn],cur[Maxn];
queue<int> q;
bool bfs(int s,int t)
{ memset(deep,0x7f,sizeof(deep));
for(int i=0;i<=n+5;i++)cur[i]=f[i];
while(!q.empty())q.pop();
deep[s]=0;
q.push(s);
while(!q.empty())
{ int now=q.front();
q.pop();
for(int i=f[now];i!=-1;i=e[i].nx)
if(e[i].w&&deep[e[i].v]>=inf)
{ deep[e[i].v]=deep[now]+1;
q.push(e[i].v);
}
}
return deep[t]<inf;
}
int dfs(int now,int t,int limit)
{ if(!limit||now==t)return limit;
int flow=0,x;
for(int i=cur[now];i!=-1;i=e[i].nx)
{ cur[now]=i;
if(deep[e[i].v]==deep[now]+1)
{ x=dfs(e[i].v,t,min(limit,e[i].w));
if(x==0)continue;
flow+=x;
limit-=x;
e[i].w-=x;
e[i^1].w+=x;
if(limit==0)break;
}
}
return flow;
}
int dinic(int s,int t)
{ int maxflow=0;
while(bfs(s,t))maxflow+=dfs(s,t,inf);
return maxflow;
}
void read(int u,int v,int w)
{ e[++ne].v=v;
e[ne].w=w;
e[ne].nx=f[u];
f[u]=ne;
}
int main()
{ memset(f,-1,sizeof(f));
int s,t;
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++)
{ int u,v,w;
scanf("%d%d%d",&u,&v,&w);
read(u,v,w);read(v,u,0);
}
printf("%d
",dinic(s,t));
return 0;
}
-
无源汇上下界可行流
给定一个有向图,有 (n) 个点 (m) 条边,每条边都有一个流量上界和一个流量下界。
在满足流量平衡情况下,求一种可行流。
设下界为 (cl(u,v)) ,上届为 (cu(u,v)) ,则对于流量 (f(u,v)) 要满足 (cl(u,v) le f(u,v) le cu(u,v)) 。
那两边同减 (cl(u,v)) 得 (0 le f(u,v)-cl(u,v) le cu(u,v)-cl(u,v)) 。
那我们不妨假设每条边先流满了 (cl(u,v)) ,然后在用容量 (cu(u,v)-cl(u,v)) 来建图。
那么建边后,就会不满足流量平衡。所以我们要通过加一些边来使他满足。
对于每一条边 ((u,v)) ,为了要让其平衡都会让点 (u) 流量增加 (cl(u,v)) ,点 (v) 流量减少 (cl(u,v)) 。
不妨用 (b[]) 来记录每个点在所有边建好后不平衡的流量。
对于 (b_x > 0) 那就连边 ((s,x)) 容量为 (b_x) 。
对于 (b_x < 0) 那就连边 ((x,t)) 容量为 (-b_x) 。
再记 $sum= sumlimits ^{n}_{i=1} b_i(b_i>0) $ 。
如果此时跑最大流的结果小于 (sum) 就是无解。 因为他的每个点的最下届情况是无法满足的。(大于 (b_x) 的点可以理解为这个点的要有可行流的最低流量)
对于每条边的流量,即为此时 dinic 跑出的流量与 (cl(u,v)) 的和。
scanf("%d%d",&n,&m);
s=n+1,t=n+2;
for(int i=1;i<=m;i++)
{ int u,v;
scanf("%d%d%d%d",&u,&v,&cl[i],&cu[i]);
a[u]-=cl[i];a[v]+=cl[i];
read(u,v,cu[i]-cl[i]);
read(v,u,0);
}
int sum=0;
for(int i=1;i<=n;i++)
if(a[i]>0)sum+=a[i],read(s,i,a[i]),read(i,s,0);
else if(a[i]<0)read(i,t,-a[i]),read(t,i,0);
int flow=dinic(s,t);
if(flow<sum)printf("NO
");
else{
printf("YES
");
for(int i=1;i<=m*2;i+=2)
printf("%d
",e[i].w+cl[i/2+1]);
}
-
有源汇上下界可行流
给定一个 (n) 个点 (m) 条边的有向图,每条边有一个容量上下限制。给定一个源点 (S) 和一个汇点 (T) ,求 (S) 到 (T) 的最大流。
考虑有源汇和无源汇的区别。
无源汇每个点都要满足流量平衡,而有源汇除了源点 (s) 和汇点 (t) 都要满足流量平衡。
利用这一点,我们可以通过加边 ((T,S)) 容量为 (inf) 的边,汇点的流量跑向源点,就可以满足流量平衡。
用上面的求无源汇的方法就可以求出有源汇上下界的可行流。(注:此时新设的源汇点为小写的 (s,t))
-
有源汇上下界最大流
呐。如果要求最大流呢?
很容易想到,可以跑完可行流后在残余网络上跑最大流,再和刚刚跑的可行流加起来。
但实际上存在一个问题,从 (s) 跑向 (t) 的最大流不一定是 (S) 到 (T) 的最大流。
所以我们要删除所有附加边,再从 (S) 到 (T) 跑最大流,最后再和之前的可行流加起来就是结果了。
memset(f,-1,sizeof(f));
int s,t,S,T;
scanf("%d%d%d%d",&n,&m,&S,&T);
s=n+1;t=n+2;
for(int i=1;i<=m;i++)
{ int u,v;
scanf("%d%d%d%d",&u,&v,&cl[i],&cu[i]);
a[u]-=cl[i];a[v]+=cl[i];
read(u,v,cu[i]-cl[i]);
read(v,u,0);
}
int sum=0;
for(int i=1;i<=n;i++)
if(a[i]>0)sum+=a[i],read(s,i,a[i]),read(i,s,0);
else if(a[i]<0)read(i,t,-a[i]),read(t,i,0);
read(T,S,inf);read(S,T,0);
if(dinic(s,t)<sum)printf("No Solution
");
else{
int res=e[ne].w;
e[ne].w=e[ne-1].w=0;
printf("%d
",res+dinic(S,T));
}
-
有源汇上下界最小流
和最大流类似,最大流是把剩下能跑的跑掉,那最小流就是把不必要的流退掉。
所以删掉附加边后在残余网络上跑最大流,但不同的是,这次是从 (T) 跑向 (S) 。 也就是最多能退回的流是多少。
然后再用可行流减去他就可以了。
memset(f,-1,sizeof(f));
int s,t,S,T;
scanf("%d%d%d%d",&n,&m,&S,&T);
s=n+1;t=n+2;
for(int i=1;i<=m;i++)
{ int u,v;
scanf("%d%d%d%d",&u,&v,&cl[i],&cu[i]);
a[u]-=cl[i];a[v]+=cl[i];
read(u,v,cu[i]-cl[i]);
read(v,u,0);
}
int sum=0;
for(int i=1;i<=n;i++)
if(a[i]>0)sum+=a[i],read(s,i,a[i]),read(i,s,0);
else if(a[i]<0)read(i,t,-a[i]),read(t,i,0);
read(T,S,inf);read(S,T,0);
if(dinic(s,t)<sum)printf("No Solution
");
else{
int res=e[ne].w;
e[ne].w=e[ne-1].w=0;
printf("%d
",res-dinic(T,S));
}
return 0;
-
最小割
对于一个网络流 (G=(V,E)) ,其割的定义为一种点的划分方式 :将所有的点划分为 (S) 和 (T=V-S) 两个集合,其中源点 (s in S) ,汇点 (t in T) 。
—— OI wiki
割 ((S,T)) 的容量 (c(S,T) = sumlimits _{u in S,v in T} c(u,v)) 。
割 ((S,T)) 的流量 (f(S,T) = sumlimits _{u in S,v in T} f(u,v) - sumlimits _{u in T,v in S} f(u,v)) 。
注意两个概念的区别。
给定一个 (n) 个点 (m) 条边的有向图,每条边给定一个容量,给定 (s) 和 (t), 求 ((S,T)) 的最小割。
解决这个问题要用到最大流最小割定理。
即: (f(s,t)_{max} = c (s,t) _{min}) 。
所以要求最小割直接转换为最大流跑一遍就好了。
以下是一个证明:
由刚刚概念得 (f(s,t) le c(s,t))
当此时 (f(s,t)) 为最大流时,则残余网络上不存在一个增广路。
也就是 (S) 的出边是满流, (S) 的入边是零流。
即 (sumlimits _{u in T,v in S} f(u,v)=0) ,那么还是由概念得此时 (f(u,v)=c(u,v)) 。
代码和刚刚的 dinic 完全一致((,所以这边不再放代码。
P2057 [SHOI2007]善意的投票 / [JLOI2010]冠军调查 个人觉得最小割基础题。
有 (n) 个小孩投票,投 (0) 的表示睡觉,投 (1) 的表示不睡觉。
如果投了自己不相投的票,或者和自己的好朋友投票不一样,都算一次冲突。
求最小冲突。
每个小孩看成一个点,这些点要么投 (0) 要么投 (1) 。
所以我们不妨自己设两个点 (s) 和 (t) 。对于第 (i) 个小孩,如果最初意愿投 (0) 就连边 ((s,i)) ,容量为 (1) ; 类似的,如果最初意愿投 (0) 就连边 ((i,t)) ,容量为 (1) 。
对于两个好朋友 (x,y) ,我们在他们之间连一条边 ((x,y)) 和 ((y,x)) ,两条边的容量都为 (1) 。
可以想象,如果这两个小朋友同属 (S) 或 (T) ,最小割是一定不会割掉他们之间的连边的。
但如果一个属于 (S) ,另一个属于 (T) ,那么 ((x,y)) 或者 ((y,x)) 一定会被割掉其中一条。特别注意的是,矛盾是双向的,所以两条边的容量都为 (1) 。
建完图后跑 dinic 就行啦。
scanf("%d%d",&n,&m);
n++;s=0;t=n;
for(int i=0;i<=n;i++)f[i]=-1;
for(int i=1;i<n;i++)
{ int x;
scanf("%d",&x);
if(x)
{ read(s,i,1);
read(i,s,0);
}
else{
read(t,i,0);
read(i,t,1);
}
}
for(int i=1;i<=m;i++)
{ int x,y;
scanf("%d%d",&x,&y);
read(x,y,1);
read(y,x,1);
}
printf("%d
",dinic(s,t));
-
最大权闭合子图
什么是闭合子图?
如果有向图 (G=(V,E)) 的导出子图 (H=G[V^ * ]) 满足 $forall v in V^* $ , ((v,u) in E) ,有 $u in V^* $ ,则称 (H) 是 (G) 的一个闭合子图。
—— OI wiki
直白的话来说,就是选一个子图,里面没有边指向外边。
如下图:

(0,2,3,4,5) 就是一个闭合子图。
现在给定每个点一个权值 (a_i) ,可能为负数,求一个闭合子图,使最大权值和最大。
考虑最小割。设 (sum= sumlimits _ {i in V, a_i >0} a_i) 。
对于原图保留,对于原图存在的一条边 ((u,v)) ,建边 ((u,v)) 容量 (c(u,v)=inf) 。
对于一个点 (x) 。如果 (a_x>0) 连边 ((s,x)) 容量为 (a_x) ,对于 (a_x<0) 连边 ((x,t)) 容量为 (-a_x) 。
然后跑最小割 (f) ,结果即为 ((sum-f)) 。
以下为证明。
引入一下新概念:简单割。 简单割是指割 ((S,T)) 中的割要么为 ((s,u)) 要么为 ((u,t)) 。
那么很显然,对于刚刚建图的最小割一定为简单割。因为它不可能去割掉中间容量为 (inf) 的边。剩下可能割的只有 ((s,u)) 或者 ((u,t)) 。
接下来证明 简单割和一个闭合子图是一一对应的。
所以对于一个简单割 (f) ,就相当于是选这些点。
那么闭合子图 (E) 和源点 (s) 构成 (S) ,剩下的点和 (t) 构成 (T) 。
如果这个对应的割 ((S,T)) 不是简单割。那么存在一个边 ((u,v)) (其中 (u in S,v in T))然后 (c(u,v)=inf) 。
说明 ((u,v)) 这条边是指向外边的,也就是因为 $ v otin S$ 说明这个图就不是闭合子图了。
与假设矛盾,所以闭合子图是简单割。
对于一个图中的简单割。图中的一个点 (u (u in S)) ,有一条边 ((u,v)) ,且容量为 (c(u,v)=inf) 。
因为是简单割,所以 (c(u,v)) 不可能是割,所以必然 (v in S) 。也就是说 (u) 的所有出边的点都是在 (S) 中。 所以对应的就是闭合子图。
所以简单割是闭合子图。
回到上面,刚刚求的最小割因为是简单割,所以最小割对应的一定是一个闭合子图,于是要证明最小割对应最大权闭合子图 。
首先对于一个割 ((S,T)) 有容量 (c(S,T) = sumlimits _ {u in S,v in T} c(u,v) = sumlimits _ {u in S,a_u<0} | a_u | + sumlimits _ {v in T,a_v>0} a_v) 。
闭合子图的权值和 (W= sumlimits _ {u in S} a_u = sumlimits _ {u in S,a_u>0} a_u - sumlimits _ {u in S,a_u<0} |a_u|) 。
所以有 (c(S,T)+W =sumlimits _ {u in S,a_u<0} | a_u | + sumlimits _ {v in T,a_v>0} a_v + sumlimits _ {u in S,a_u>0} a_u - sumlimits _ {u in S,a_u<0} |a_u|)
(c(S,T)+W = sumlimits _ {v in T,a_v>0} a_v + sumlimits _ {u in S,a_u>0} a_u) 。
所以 (W=sumlimits _ {u in S,a_u>0} a_u + sumlimits _ {v in T,a_v>0} a_v - c(S,T)=sum-c(S,T)) 。
所以最小割即 (c(S,T)) 最小时,有 (W) 最大。
证毕。
-
费用流
模板题:link.
什么流水要收费了。给定一个 (n) 个点 (m) 条边的有向图,每条边给一个容量和一个费用 。求 (s) 到 (t) 的最大流,且要求在流是最大流的情况下,费用最小。
其实最大流的本质没变,要解决的就是费用最小这个问题。
那么在每次寻找增广路时,就要寻找费用最小。所以就可以考虑用 spfa 来求。需要注意的是,用 spfa 求的边长为费用。
这里代码用的是 EK 算法,
但是我自己看的也难受,大概可能以后会补上 dinic 算法(?咕)我刚写完上句话就被费用流 EK 卡成 TLE (。)
然后就是,因为费用流和最大流的差不多就是多了一个费用,所以一些模型都非常相似。
这里不再单独讲述。
//这个是 EK
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<queue>
using namespace std;
const int Maxn=5000+5,Maxm=50000+5;
const int inf=1e9;
int n,m,ne=-1,s,t,f[Maxn];
int maxflow,mincost,dis[Maxn],incf[Maxn],pre[Maxn];
bool vis[Maxn];
queue<int>q;
struct edge{
int v,w,c,nx;
}e[Maxm<<1];
void read(int u,int v,int w,int c)
{ e[++ne].v=v;
e[ne].w=w;
e[ne].c=c;
e[ne].nx=f[u];
f[u]=ne;
}
bool spfa()
{ for(int i=0;i<=n;i++)dis[i]=inf;
memset(vis,0,sizeof(vis));
q.push(s);
dis[s]=0;vis[s]=1;
incf[s]=inf;
while(!q.empty())
{ int u=q.front();
q.pop();
vis[u]=0;
for(int i=f[u];i!=-1;i=e[i].nx)
{ int v=e[i].v;
if(e[i].w==0)continue;
if(dis[u]+e[i].c<dis[v])
{ dis[v]=dis[u]+e[i].c;
incf[v]=min(incf[u],e[i].w);
pre[v]=i;
if(!vis[v])q.push(v),vis[v]=1;
}
}
}
return (dis[t]<inf);
}
void MCMF()
{ while(spfa())
{ int i,x=t;
maxflow+=incf[t];
mincost+=dis[t]*incf[t];
while(x!=s)
{ i=pre[x];
e[i].w-=incf[t];
e[i^1].w+=incf[t];
x=e[i^1].v;
}
}
}
int main()
{ memset(f,-1,sizeof(f));
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++)
{ int u,v,w,c;
scanf("%d%d%d%d",&u,&v,&w,&c);
read(u,v,w,c);
read(v,u,0,-c);
}
MCMF();
printf("%d %d
",maxflow,mincost);
return 0;
}