拉格朗日乘子 是什么
一、总结
一句话总结:
基本的【拉格朗日乘子法(又称为拉格朗日乘数法)】,就是【求函数 f(x1,x2,...) 在 g(x1,x2,...)=0 的约束条件下的极值】的方法。
其【主要思想】是引入一个【新的参数 λ (即拉格朗日乘子】),将【约束条件函数与原函数联系】到一起,使能【配成与变量数量相等的等式方程】,从而求出得到原函数极值的各个变量的解。
1、拉格朗日乘数法(Lagrange multiplier)的几何意义?
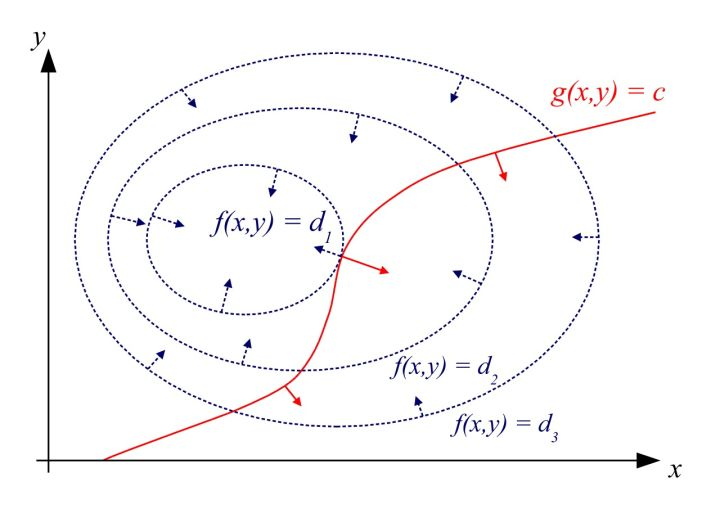
我们可以画出f的等高线图,如下图。此时,约束g=c由于只有一个自由度,因此也是图中的一条曲线(红色曲线所示)。
显然地,【当约束曲线g=c与某一条等高线f=d1【相切】时,函数f取得极值】。两曲线相切等价于两曲线在切点处拥有【共线的法向量】。因此可得函数f(x,y)与g(x,y)在切点处的梯度(gradient)成正比。
于是我们便可以列出方程组求解【切点的坐标(x,y)】,进而得到函数【f的极值】。
二、拉格朗日乘子 是什么
博客对应课程的视频位置:
1、先来看看百度百科的说法
https://baike.baidu.com/item/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E5%AD%90/4841841?fr=aladdin
基本的拉格朗日乘子法(又称为拉格朗日乘数法),就是求函数 f(x1,x2,...) 在 g(x1,x2,...)=0 的约束条件下的极值的方法。其主要思想是引入一个新的参数 λ (即拉格朗日乘子),将约束条件函数与原函数联系到一起,使能配成与变量数量相等的等式方程,从而求出得到原函数极值的各个变量的解。拉格朗日乘子是数学分析中同一名词的推广。
2、来看看知乎的说法
https://www.zhihu.com/question/38586401
拉格朗日乘数法(Lagrange multiplier)有很直观的几何意义。
举个2维的例子来说明:
假设有自变量x和y,给定约束条件g(x,y)=c,要求f(x,y)在约束g下的极值。
我们可以画出f的等高线图,如下图。此时,约束g=c由于只有一个自由度,因此也是图中的一条曲线(红色曲线所示)。显然地,当约束曲线g=c与某一条等高线f=d1相切时,函数f取得极值。
两曲线相切等价于两曲线在切点处拥有共线的法向量。因此可得函数f(x,y)与g(x,y)在切点处的梯度(gradient)成正比。
于是我们便可以列出方程组求解切点的坐标(x,y),进而得到函数f的极值。