在做关于数组的算法题之前,一定要先对数组有一定的了解: C#中的数组一旦被创建,大小就固定了,且不支持动态数组。数组的索引是从0开始的,也就是说,一个长度为n的数组,索引为0~(n-1)。
数组实例是从System.Array继承的对象,数组是引用类型,有数据的引用及数据对象本身,引用在栈或堆上,且数组本身总是在堆上。
数组是引用类型,但数组的元素可以是值类型或引用类型,如果存储在数组中的元素都是值类型,则数组被称为值类型数组。如果存储在数组中的元素都是引用类型对象,数组则被称为引用类型数组。
合并数组的算法一般分为两种,一种是两个有序数组的合并,合并完后保证数组依然有序,还有一种是两个数组合并并对合并的数组进行排序。
毫无疑问,第二种算法比较简单,但是,很多人会将第一种情况的处理也同样使用第二种情况的算法,这不能说是错误,但,算法的效率却大大的降低了,为什么?本来两个数组都是有序的,一合并,原本有序的有利条件被打破了。那么,应该怎么做才能保证有利条件对我们有帮助呢?下面将两个算法分开阐述。
先说第二种情况吧,本身数组就是无序的,但合并后要保证数组有序,怎么做?最简单的思维,反正源数组也是无序的,那么干脆直接合并两个数组,再对新数组进行一个排序。
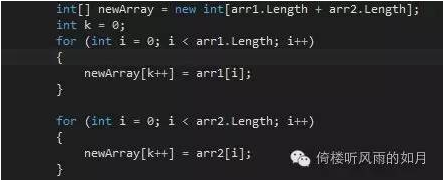
先说合并数组吧,定义一个新数组,长度为两个数组(arr1, arr2)的长度之和,再定义新数组的索引,然后使用两个for循环即可完成:
排序的算法有很多的选择,最简单的冒泡,插入,选择……这里给出冒泡和插入的算法实现,排序原理不赘述了,不了解的通过各种渠道去找寻答案吧~
也就是说,只需要在代码里再调用相应的排序算法即可,全部代码如下:
使用了两个for循环将两个数组合并称为一个新数组,时间复杂度为O(N), 而无论是冒泡还是插入排序,平均的时间复杂度都是O(N*N), 因此,这种情况下算法的时间复杂度为O(N*N).
说完无序数组的合并且排序之后,回到第一种情况,两个有序数组的排序进行合并,且保证合并后的数组依然有序,前面说过了,如果使用第二种情况的解决方法当然没问题,但是时间复杂度是O(N*N), 从算法效率上来说,并非最佳算法,而与此同时,我们忽略了题目给到我们的有利条件:数组本身是有序的。
这个有利的条件如何利用,才能让算法效率更高呢?同样的,我们需要定义一个新数组来存储两个数组合并后的结果,如何插入元素是我们需要动脑筋的,有没有一个办法,让两个数组中的数据从小到大插入新数组呢?当然有办法。
取出数组A的第一个元素和数组B的第一个元素,比较,如果A[0]<B[0], 则,A[0]插入到新数组C[0]的位置,然后用A[1] 继续与B[0] 进行比较,如果A[1]<B[0], 则,A[1]继续向新数组插入数据,反之,则B[0]向新数组插入数据,依次循环,将两个数组的元素插入新数组:
这样就大功告成了? hey, 等等,如果数组A中的元素都加到新数组中了,数组B中还有元素怎么办?或者反过来,数组B中的元素都加到新数组中了,但数组A中还有元素怎么办?没错,由于数组是有序的,这时候,可以完全放心地把剩下的元素直接插入新数组中,因此,这里需要有两种情况,第一,还存在数组A中的待插入元素,第二,还存在数组B中的待插入元素,很简单,只需要遍历剩下的所有元素,将其一一加入到新数组即可。
因此,整个算法的代码应该如下:
再看看这个算法的时间复杂度,没有嵌套的循环,算法复杂度为O(N), 比第二种情况的效率高了一倍,看来待合并数组是否有序这个条件,真的很重要啊~~
更多内容可以扫描下面二维码关注微信公众号
