AtCoder Beginner Contest 185 题解

A - ABC Preparation

排序找出最小值

int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    vector<int> a(4);
    for (auto &i : a) cin >> i;
    sort(a.begin(), a.end());
    cout << a[0];
    return 0;
}

B - Smartphone Addiction

模拟

int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    int N, M, T, A, B, K = 0, t = 0;
    cin >> N >> M >> T;
    for (M = N; cin >> A >> B; N += B + K - 2 * A, K = B, N = min(N, M))
        if (N - A + K <= 0) t++;
    cout << (N - T + B <= 0 || t ? "No" : "Yes");
    return 0;
}

C - Duodecim Ferra

组合数学问题，裁点有 L-1 个，我们取其中的 11 个，根据组合答案为：(C_{L-1}^{11})。

然后根据组合数学原来进行化简 ↓

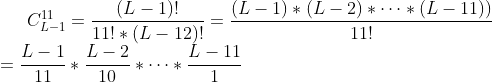
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    ll L, i = 0, N = 1;
    for (cin >> L; ++i < 12; N *= (L - i), N /= i)
        ;
    cout << N << "
";
    return 0;
}

D - Stamp

计算出所有白色区间。最短的区间长度即为 (k) 的最佳取值，之后计算需要的邮票总数即可。

好题！

int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    int N, M, K = 0, cnt = 0, i = 1;
    cin >> N >> M;
    int A[M + 2], B[M + 1];
    A[0] = 0, A[M + 1] = N + 1;
    for (; i <= M; ++i) cin >> A[i];
    sort(A, A + M + 2);
    for (int i = 0; i < M + 1; ++i) B[i] = A[i + 1] - A[i] - 1;
    sort(B, B + M + 1);

    // for (int i = 0; i < M + 1; ++i) cout << B[i] << " ";
    // cout << endl;

    for (i = 0; i < M + 1; ++i) {
        if (!K) K = B[i];
        if (K) cnt += (B[i] + K - 1) / K;
    }
    cout << cnt << "
";
    return 0;
}

E - Sequence Matching

类似于最长公共子序列。考虑 (dp[i-1][j],dp[i][j-1],dp[i-1][j-1])三种转移。

时间复杂度(mathcal{O}(NM))。

// 暂无

F - Range Xor Query

线段树，单点更新，区间查询。直接用 AC-Library 模板即可。

时间复杂度 (mathcal{O}((N+Q)log N))。

#include <bits/stdc++.h>

#include <atcoder/segtree>
using namespace std;
int op(int a, int b) { return a ^ b; }
int e() { return 0; }
int main() {
    int n, q;
    cin >> n >> q;
    vector<int> v(n);
    for (int i = 0; i < n; ++i) cin >> v[i];
    atcoder::segtree<int, op, e> seg(v);
    while (q--) {
        int t, x, y;
        cin >> t >> x >> y;
        if (t == 1) {
            seg.set(x - 1, v[x - 1] ^ y);
            v[x - 1] ^= y;
        } else {
            cout << seg.prod(x - 1, y) << endl;
        }
    }
}