蓝桥杯历年国赛真题汇总:Here
1.方格填数
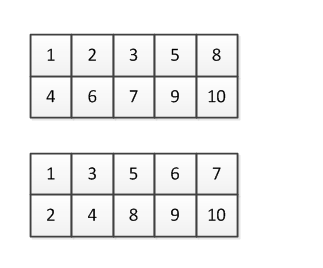
在2行5列的格子中填入1到10的数字。
要求:
相邻的格子中的数,右边的大于左边的,下边的大于上边的。
如【图1.png】所示的2种,就是合格的填法。
请你计算一共有多少种可能的方案。
请提交该整数,不要填写任何多余的内容(例如:说明性文字)。
答案:560
万能的全排列
2.四阶幻方
把1~16的数字填入4x4的方格中,使得行、列以及两个对角线的和都相等,满足这样的特征时称为:四阶幻方。
四阶幻方可能有很多方案。如果固定左上角为1,请计算一共有多少种方案。
比如:
1 2 15 16
12 14 3 5
13 7 10 4
8 11 6 9
以及:
1 12 13 8
2 14 7 11
15 3 10 6
16 5 4 9
就可以算为两种不同的方案。
请提交左上角固定为1时的所有方案数字,不要填写任何多余内容或说明文字。
答案:416
题意:就是左上角固定填好1,其他位置填数,每个数只能填一次,然后每行,每列,两条对角线的和都相等就算符合条件,求出一共有多少种符合条件的方案
思路:DFS再剪枝下,这题是填空题,最后直接输出即可
这道题跑全排列是跑不出答案的,只能DFS剪枝 15!= 1307674368000
int a[5][5];
bool vis[17];
int sum = 34;
int ans = 0;
bool jd(int i ) { // 检查行
int num = 0;
for (int j = 0; j < 4; ++j)num += a[i][j];
if (num != sum)return false;
return true;
}
bool check() {
int num1 = a[0][0] + a[1][1] + a[2][2] + a[3][3];
if (num1 != sum)return false;
int num2 = a[0][3] + a[1][2] + a[2][1] + a[3][0];
if (num2 != sum)return false;
for (int i = 0; i < 4; ++i) // 检查行
if (!jd(i))return false;
for (int j = 0; j < 4; ++j) { // 检查列
int k = a[0][j] + a[1][j] + a[2][j] + a[3][j];
if (k != sum)return false;
}
return true;
}
void dfs(int n) {
if (n == 16) {
if (check())++ans;
return ;
}
// 剪枝
if (n % 4 == 0 and !jd(n / 4 - 1))return ;
for (int i = 2; i <= 16; ++i) {
if (!vis[i]) {
vis[i] = true;
a[n / 4][n % 4] = i;
dfs(n + 1);
vis[i] = false;
}
}
}
void solve() {
a[0][0] = 1;
dfs(1);
cout << ans; // 416
}
3.显示二叉树
排序二叉树的特征是:
某个节点的左子树的所有节点值都不大于本节点值。
某个节点的右子树的所有节点值都不小于本节点值。
为了能形象地观察二叉树的建立过程,小明写了一段程序来显示出二叉树的结构来。
#include <stdio.h>
#include <string.h>
#define N 1000
#define HEIGHT 100
#define WIDTH 1000
struct BiTree
{
int v;
struct BiTree* l;
struct BiTree* r;
};
int max(int a, int b)
{
return a>b? a : b;
}
struct BiTree* init(struct BiTree* p, int v)
{
p->l = NULL;
p->r = NULL;
p->v = v;
return p;
}
void add(struct BiTree* me, struct BiTree* the)
{
if(the->v < me->v){
if(me->l==NULL) me->l = the;
else add(me->l, the);
}
else{
if(me->r==NULL) me->r = the;
else add(me->r, the);
}
}
//获得子树的显示高度
int getHeight(struct BiTree* me)
{
int h = 2;
int hl = me->l==NULL? 0 : getHeight(me->l);
int hr = me->r==NULL? 0 : getHeight(me->r);
return h + max(hl,hr);
}
//获得子树的显示宽度
int getWidth(struct BiTree* me)
{
char buf[100];
sprintf(buf,"%d",me->v);
int w = strlen(buf);
if(me->l) w += getWidth(me->l);
if(me->r) w += getWidth(me->r);
return w;
}
int getRootPos(struct BiTree* me, int x){
return me->l==NULL? x : x + getWidth(me->l);
}
//把缓冲区当二维画布用
void printInBuf(struct BiTree* me, char buf[][WIDTH], int x, int y)
{
int p1,p2,p3,i;
char sv[100];
sprintf(sv, "%d", me->v);
p1 = me->l==NULL? x : getRootPos(me->l, x);
p2 = getRootPos(me, x);
p3 = me->r==NULL? p2 : getRootPos(me->r, p2+strlen(sv));
buf[y][p2] = '|';
for(i=p1; i<=p3; i++) buf[y+1][i]='-';
for(i=0; i<strlen(sv); i++) buf[y+1][p2+i]=sv[i];
if(p1<p2) buf[y+1][p1] = '/';
if(p3>p2) buf[y+1][p3] = '\';
if(me->l) printInBuf(me->l,buf,x,y+2);
if(me->r) ____________________________________; //填空位置
}
void showBuf(char x[][WIDTH])
{
int i,j;
for(i=0; i<HEIGHT; i++){
for(j=WIDTH-1; j>=0; j--){
if(x[i][j]==' ') x[i][j] = '�';
else break;
}
if(x[i][0]) printf("%s
",x[i]);
else break;
}
}
void show(struct BiTree* me)
{
char buf[HEIGHT][WIDTH];
int i,j;
for(i=0; i<HEIGHT; i++)
for(j=0; j<WIDTH; j++) buf[i][j] = ' ';
printInBuf(me, buf, 0, 0);
showBuf(buf);
}
int main()
{
struct BiTree buf[N]; //存储节点数据
int n = 0; //节点个数
init(&buf[0], 500); n++; //初始化第一个节点
add(&buf[0], init(&buf[n++],200)); //新的节点加入树中
add(&buf[0], init(&buf[n++],509));
add(&buf[0], init(&buf[n++],100));
add(&buf[0], init(&buf[n++],250));
add(&buf[0], init(&buf[n++],507));
add(&buf[0], init(&buf[n++],600));
add(&buf[0], init(&buf[n++],650));
add(&buf[0], init(&buf[n++],450));
add(&buf[0], init(&buf[n++],440));
add(&buf[0], init(&buf[n++],220));
show(&buf[0]);
return 0;
}
对于上边的测试数据,应该显示出:
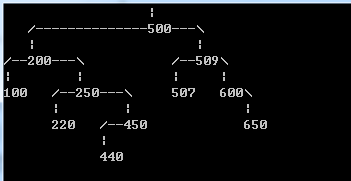
请分析程序逻辑,填写划线部分缺失的代码。
注意,只填写缺少的部分,不要填写已有的代码或符号,也不要加任何说明文字。
答案:
printInBuf(me->r, buf, p2 + strlen(sv), y + 2);分析:比着上面的左子树的代码,if(me->l) printInBuf(me->l,buf,x,y+2);
y代表的层数,x代表的列,只需要调整右子树的x位置的值即可,试出来的。
4.穿越雷区
X星的坦克战车很奇怪,它必须交替地穿越正能量辐射区和负能量辐射区才能保持正常运转,否则将报废。
某坦克需要从A区到B区去(A,B区本身是安全区,没有正能量或负能量特征),怎样走才能路径最短?
已知的地图是一个方阵,上面用字母标出了A,B区,其它区都标了正号或负号分别表示正负能量辐射区。
例如:
A + - + -
- + - - +
- + + + -
+ - + - +
B + - + -
坦克车只能水平或垂直方向上移动到相邻的区。
数据格式要求:
输入第一行是一个整数n,表示方阵的大小, 4<=n<100
接下来是n行,每行有n个数据,可能是A,B,+,-中的某一个,中间用空格分开。
A,B都只出现一次。
要求输出一个整数,表示坦克从A区到B区的最少移动步数。
如果没有方案,则输出-1
例如:
用户输入:
5
A + - + -
- + - - +
- + + + -
+ - + - +
B + - + -
则程序应该输出:
10
资源约定:
峰值内存消耗 < 512M
CPU消耗 < 1000ms
#include<bits/stdc++.h>
using namespace std;
int Min = 99999999; //用来更新最小值
int a[101][101], book[101][101]; //book标记走过的路
int x, y, x2, y2; //(x,y)标记A的坐标、(x2,y2)标记B的坐标。
int n;//矩阵大小n*n
char s;//存储临时字符
void dfs(int x, int y, int step) {
int next[4][2] = {{0, 1}, {1, 0}, { -1, 0}, {0, -1}}; //定义方向数组
int tx, ty; //定义下一个要搜索的坐标
for (int i = 0; i <= 3;
i++) { //循环(x,y)的右下左上坐标
tx = x + next[i][0];
ty = y + next[i][1];
//超出边界即跳过本次循环执行下一次
if ( tx > n || ty > n || tx < 1 || ty < 1)
continue;
if (tx == x2
&& ty == y2) { //这里之所以把满足条件更新Min放在循环内是因为下面的B点没有办法被搜素到,所以用下一个将要搜索的点来判断,step+1也是因为B点没有被dfs所以要加1.
if (step + 1 < Min)
Min = step + 1;
return;
}
int p;
p = a[x][y];
p = 0 - p; //这个p就是本题的重点了,(p==0 && step==0)就是特判从A点进入辐射区。然后就是如果搜索到了B点该怎么办?我们知道B点的状态是a[tx][ty]=0,B点的0肯定和辐射区的1、-1不相等,所以B点不能进入dfs。
if ((a[tx][ty] == p && book[tx][ty] == 0) || (p == 0 && step == 0)) {
book[tx][ty] = 1; //标记走过的点
dfs(tx, ty, step + 1);
book[tx][ty] = 0; //一次深搜结束后取消标记
}
}
return;//回溯,如果到这个点上下左右都不能走,回到上一个点。
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
cin >> s;
if (s == '+')
a[i][j] = 1;
if (s == '-')
a[i][j] = -1;
if (s == 'A') {
x = i; y = j;
}
if (s == 'B') {
x2 = i; y2 = j;
}
}
//处理矩阵并且标记A、B坐标。
dfs(x, y, 0); //从A的坐标开始搜索。
if (Min == 99999999) {
cout << -1;
} else
cout << Min;
return 0;
}
5.切开字符串
Pear有一个字符串,不过他希望把它切成两段。
这是一个长度为N(<=10^5)的字符串。
Pear希望选择一个位置,把字符串不重复不遗漏地切成两段,长度分别是t和N-t(这两段都必须非空)。
Pear用如下方式评估切割的方案:
定义“正回文子串”为:长度为奇数的回文子串。
设切成的两段字符串中,前一段中有A个不相同的正回文子串,后一段中有B个不相同的非正回文子串,则该方案的得分为A*B。
注意,后一段中的B表示的是:“...非正回文...”,而不是: “...正回文...”。
那么所有的切割方案中,A*B的最大值是多少呢?
【输入数据】
输入第一行一个正整数N(<=10^5)
接下来一行一个字符串,长度为N。该字符串仅包含小写英文字母。
【输出数据】
一行一个正整数,表示所求的A*B的最大值。
【样例输入】
10
bbaaabcaba
【样例输出】
38
【数据范围】
对于20%的数据,N<=100
对于40%的数据,N<=1000
对于100%的数据,N<=10^5
解题思路:
1.先枚举前后串的分割情况,每枚举出一种情况就分别对前串和后串进行处理
2.处理过程:计算前串的子串正回文个数,计算后串的子串不是正回文的个数
(注意:后串的子串只要不符合正回文都算一种情况,即它可以是非回文,可以是偶数长度回文。处理的时候我们只需要用一个check函数检测是不是正回文,前串统计返回值是1的情况,后串统计返回值是0的情况)
一开始我被误导了,以为后串的“非正回文子串”是偶数长度的回文子串
3.每处理完一种分割情况就尝试能否更新最大值
注意事项:题目要求计算的是不相同的子串,可以用一个map来查重
int n, A, B, max_ans = -1;
string s, a, b;
int check(string
str) { //用于检测字符串是否是正回文子串
if (str.length() % 2 == 0) { //如果长度是奇数,直接判错
return 0;
}
for (int i = 0; i < str.length() / 2;
i++) { //如果不是回文,直接判错
if (str[i] != str[str.length() - 1 - i])
return 0;
}
return 1;
}
int f_front(string ss) {
map<string, int> mp; //用于标记字符串是否出现过
int ans = 0;
string temp;
for (int i = 0; i < ss.length(); i++) { //枚举子串起点
for (int j = 1; j <= ss.length(); j++) { //枚举子串长度
temp = ss.substr(i, j);
if (check(temp)
&& !mp.count(
temp)) { //如果这个串是正回文并且没有出现过
mp[temp] = 1;
ans++;
}
}
}
return ans;
}
int f_rear(string ss) {
map<string, int> mp; //用于标记字符串是否出现过
int ans = 0;
string temp;
for (int i = 0; i < ss.length(); i++) { //枚举子串起点
for (int j = 1; j <= ss.length(); j++) { //枚举子串长度
temp = ss.substr(i, j);
if (!check(temp)
&& !mp.count(
temp)) { //如果这个串不是正回文并且没有出现过
mp[temp] = 1;
ans++;
}
}
}
return ans;
}
void sovle() {
cin >> n >> s;
for (int i = 1; i <= s.length() - 1; i++) { //枚举前串的长度
a = s.substr(0, i); //前串,起点是0,长度是i
b = s.substr(i, s.length() -
i); //后串,起点是i,长度是length-i
//cout << "前串:"+a << endl <<"后串:"+ b <<endl;
A = f_front(a);
B = f_rear(b);
if (A * B > max_ans) {
max_ans = A * B;
}
}
cout << max_ans << endl;
}
6.铺瓷砖
为了让蓝桥杯竞赛更顺利的进行,主办方决定给竞赛的机房重新铺放瓷砖。机房可以看成一个n*m的矩形,而这次使用的瓷砖比较特别,有两种形状,如【图1.png】所示。在铺放瓷砖时,可以旋转。
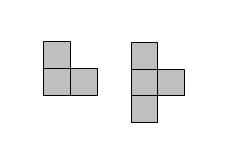
主办方想知道,如果使用这两种瓷砖把机房铺满,有多少种方案。
【输入格式】
输入的第一行包含两个整数,分别表示机房两个方向的长度。
【输出格式】
输出一个整数,表示可行的方案数。这个数可能很大,请输出这个数除以65521的余数。
【样例输入1】
4 4
【样例输出1】
2
【样例说明1】
这两种方案如下【图2.png】所示:
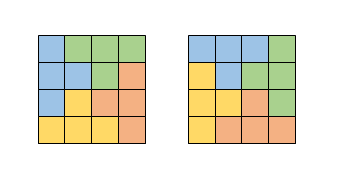
【样例输入2】
2 6
【样例输出2】
4
【数据规模与约定】
对于20%的数据,1<=n, m<=5。
对于50%的数据,1<=n<=100,1<=m<=5。
对于100%的数据,1<=n<=10^15,1<=m<=6。
待补