【每日一题】31.「土」秘法地震 (二维前缀和 / DP)

补题链接：Here

题意就是要找每一个 (k * k) 的小正方形里至少有一个1的数量

显然我们可以通过二维前缀和处理出(1, 1) 到 (n, m) 的数量

然后通过枚举处理出答案，具体思想是容斥

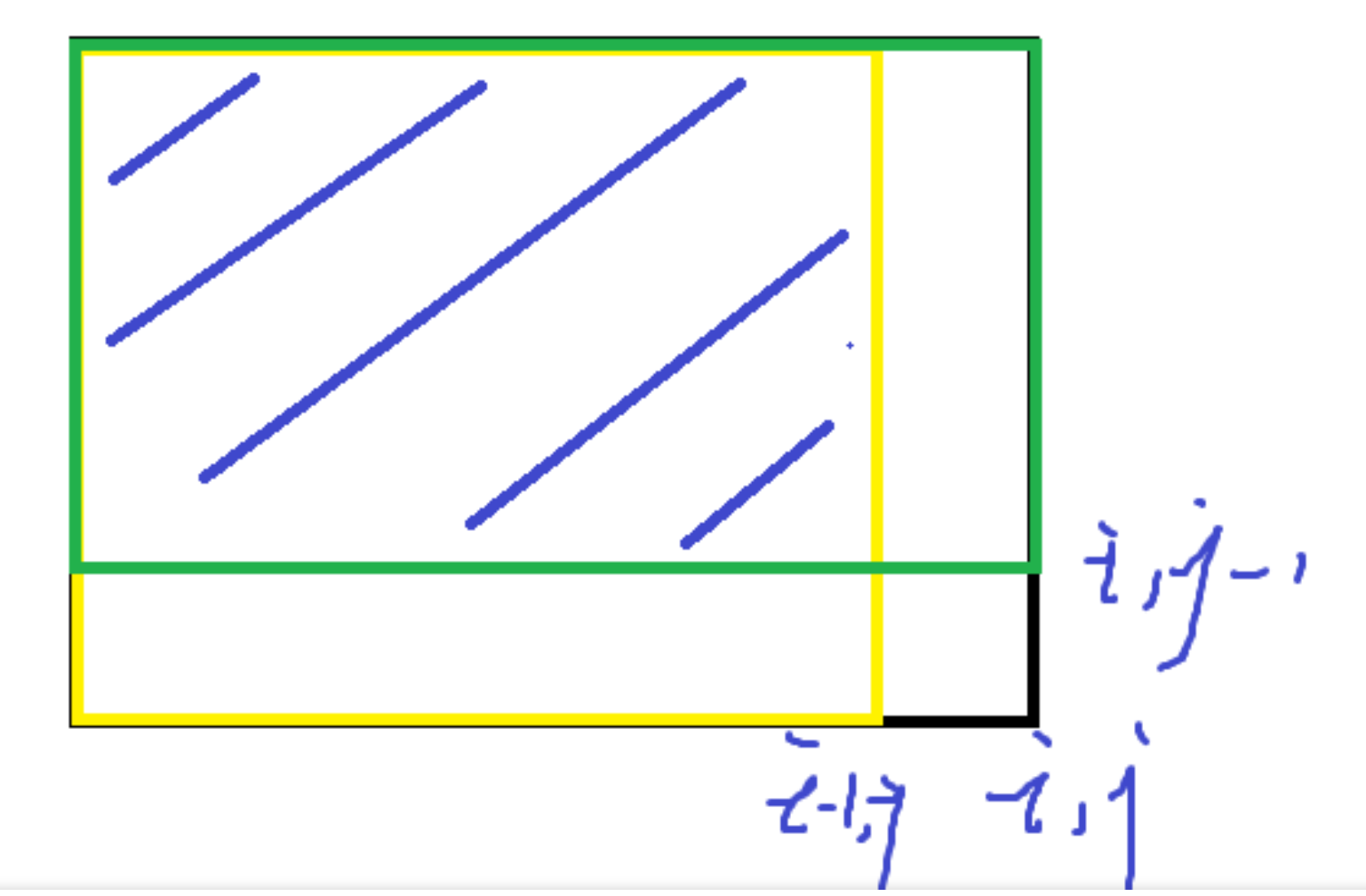
令 (dp[i][j]) 为 (1, 1) 到 (n, m) 的1的数量

有递推式子 (dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + pos_{i,j} == '1')

这个式子可以看成以下图形

【AC代码】

const int N = 2e3 + 10;
int dp[1010][1010];
void solve() {
	int n, m, k;
	cin >> n >> m >> k;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j) {
			char ch; cin >> ch;
			dp[i][j] += (ch == '1');
		}
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
			dp[i][j] += dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
	int ans = 0;
	for (int i = k; i <= n; i++)
		for (int j = k; j <= m; j++)
			if (dp[i][j] - dp[i - k][j] - dp[i][j - k] + dp[i - k][j - k] > 0)
				ans++;
	cout << ans << "
";
}

这道题和蓝书上前缀和专题的一道题很像