人工智能主要分支
人工智能,机器学习,深度学习
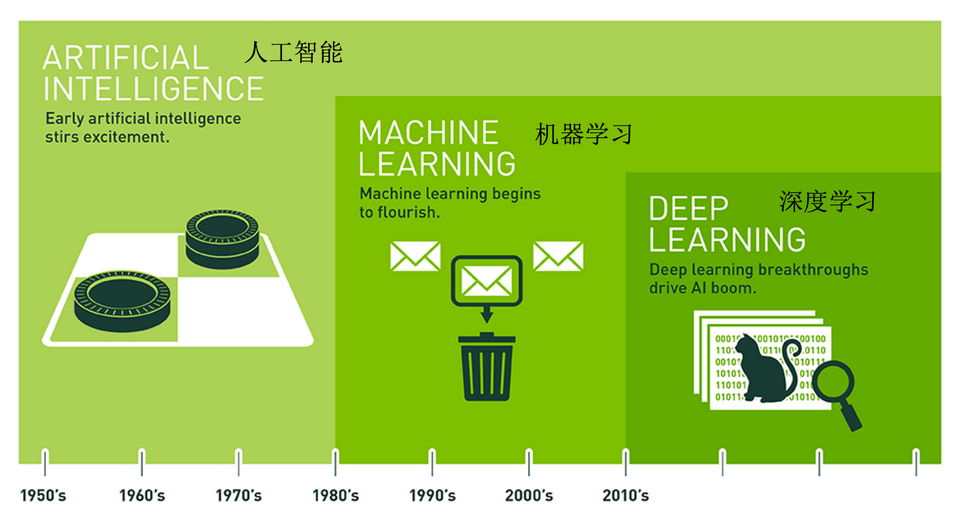
机器学习是人工智能的一个实现途径,深度学习是机器学习的一个子集.
主要分支介绍
通讯,感知与行动是现代人工智能的三个关键能力,在这里我们将根据这些能力/应用对这三个技术领域进行介绍:
(1) 计算机视觉(CV)
(2) 自然语言处理(NPL)
(3) 机器人
人工智能发展必备三要素
(1) 数据
(2) 算法
(3) 计算力
机器学习工作流程
什么是机器学习
机器学习是从数据中自动分析获得模型,并利用模型对未知数据进行预测.
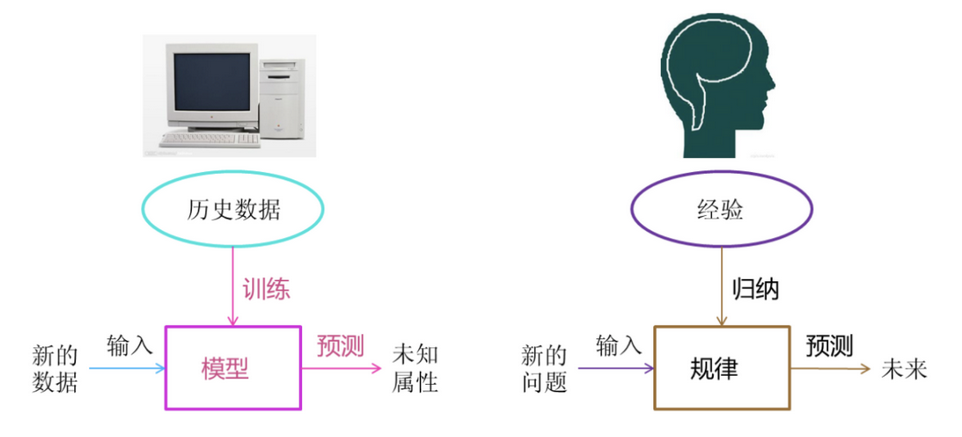
机器学习工作流程
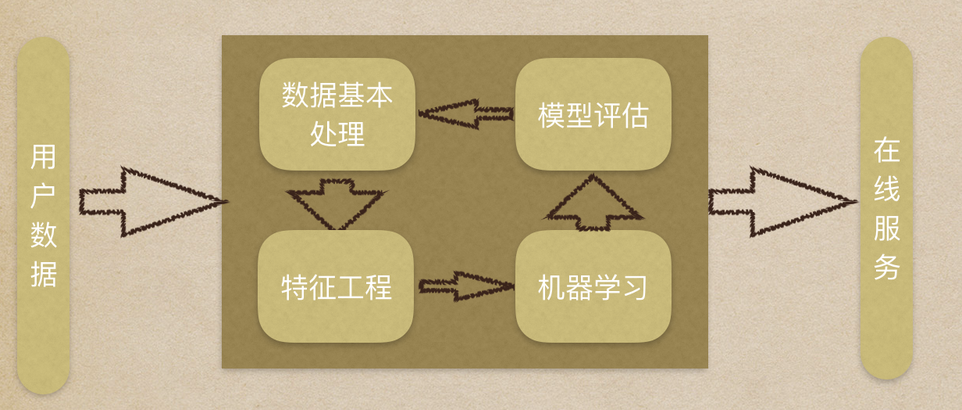
机器学习工作流程总结:
(1) 获取数据集
(2) 数据基本处理
(3) 特征工程
(4) 机器学习(模型训练)
(5) 模型评估
数据集介绍
数据类型构成
数据类型一: 特征值+目标值(目标值是连续的和离散的)
数据类型二: 只有特征值,没有目标值
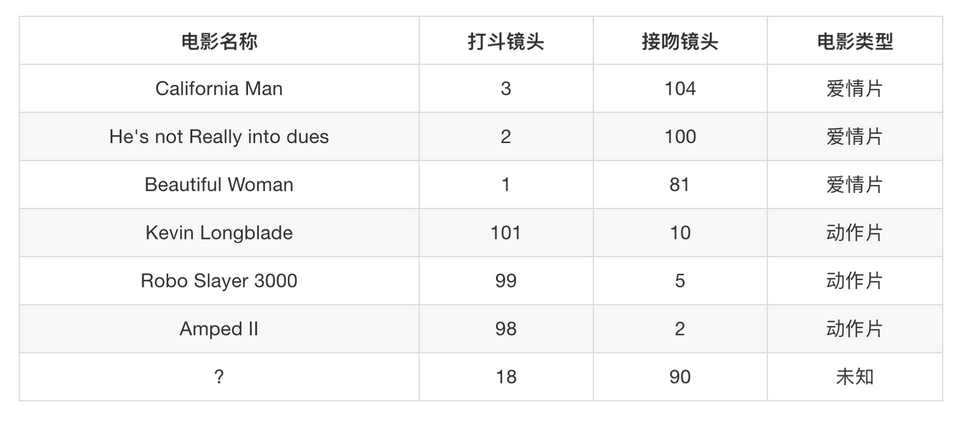
下图是数据类型一,有特征值也有目标值.
通过一系列特征值,也就是各种镜头的数目,可以得到电影的类型是什么.
下面是数据类型二,只有特征值,没有目标值.
如果对下面的人进行分类的话,不同人有不同的分类方法.
可以按照有没有带帽子分类,可以按照手上有没有拿东西分类...

数据简介
在数据集中,一般:
(1) 一行数据我们称为一个样本
(2) 一列数据我们称为一个特征
(3) 有些数据有目标值(标签值),有些数据没有目标值
数据分割
机器学习一般的数据集会划分为两个部分:
(1) 训练数据: 用于训练,构建模型
(2) 测试数据: 在模型检验时使用,用于评估模型是否有效
划分比例:
测试集: 0.7~0.8
测试集: 0.2~0.3
数据基本处理
数据基本处理: 即对数据的缺失值,重复值,异常值进行一个处理.
特征工程
什么是特征工程
特征工程: 使用专业背景知识和技巧处理数据,使得特征能在机器学习算法上发挥更好的作用.
意义: 会直接影响机器学习的效果.
为什么需要特征工程
业界广泛流传: 数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已.
特征工程包含
(1) 特征提取
(2) 特征预处理
(3) 特征降维
特征提取
特征提取: 将任意数据(如文本或图像)转换为可用于机器学习的数字特征.
如下图,需要要文本信息转化为算法模型能够使用的数字特征.

特征预处理
特征预处理: 通过一些转换函数将特征数据转换成更加适合算法模型的特征数据.
下图展示的是对数据进行归一化操作.
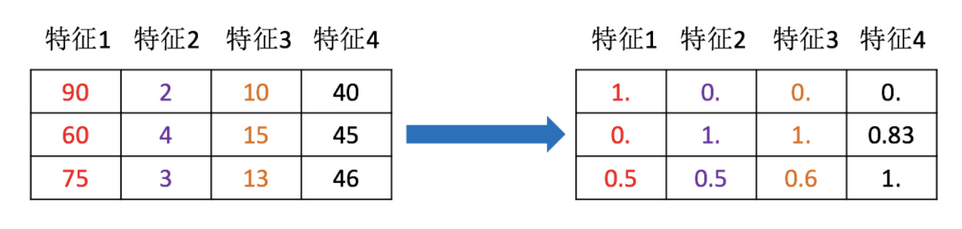
特征降维
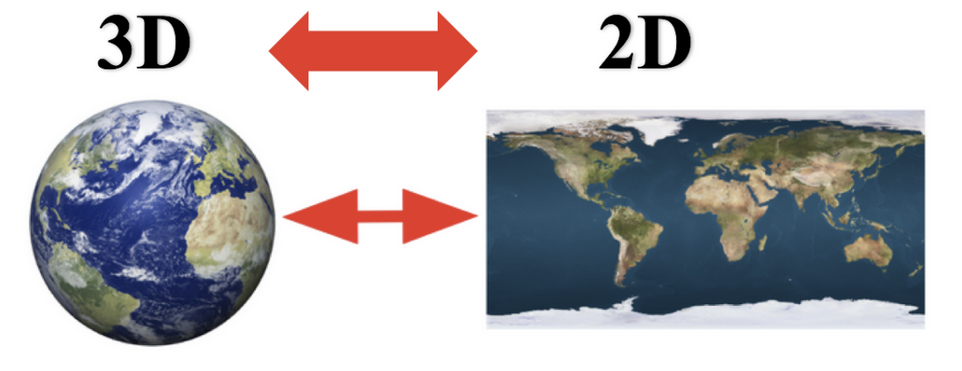
特征降维: 指在某些限定条件下,降低随机变量(特征)个数,得到一组"不相关"主变量.
机器学习算法分类
机器学习类型的分类依据是: 数据集的特征值和目标值
监督学习
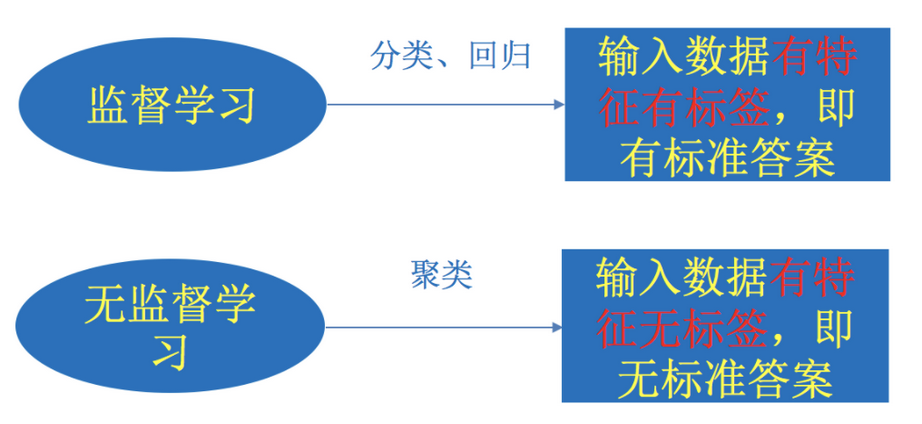
定义: 输入数据既有特征值,也有目标值.
函数的输出是一个连续值,则是回归问题.
函数的输出是一个离散值,则是分类问题.
回归问题
例如: 预测房价,根据样本集拟合出一条连续曲线
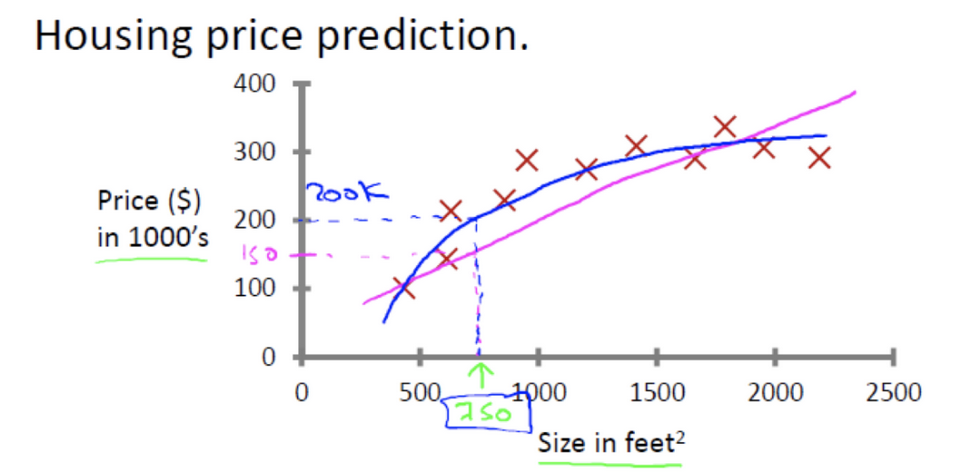
分类问题
例如: 根据肿瘤特征判断良性还是恶性,是离散的结果.
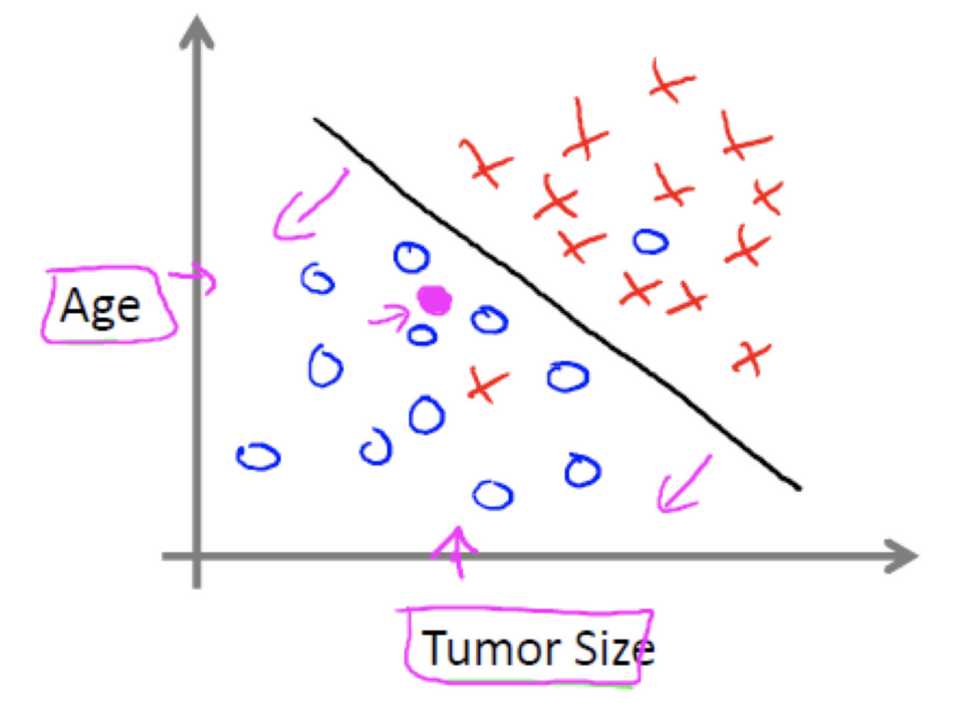
无监督学习
定义: 输入数据只有特征值.
输入数据没有被标记,也没有确定结果.
样本数据类别未知,需要根据样本间的相似性对样本集进行分类(聚类,clustering)试图使类内差距最小化,类间差距最大化.
例如对下图的人进行分类,就没有唯一的一个分类标准.

有监督,无监督算法对比
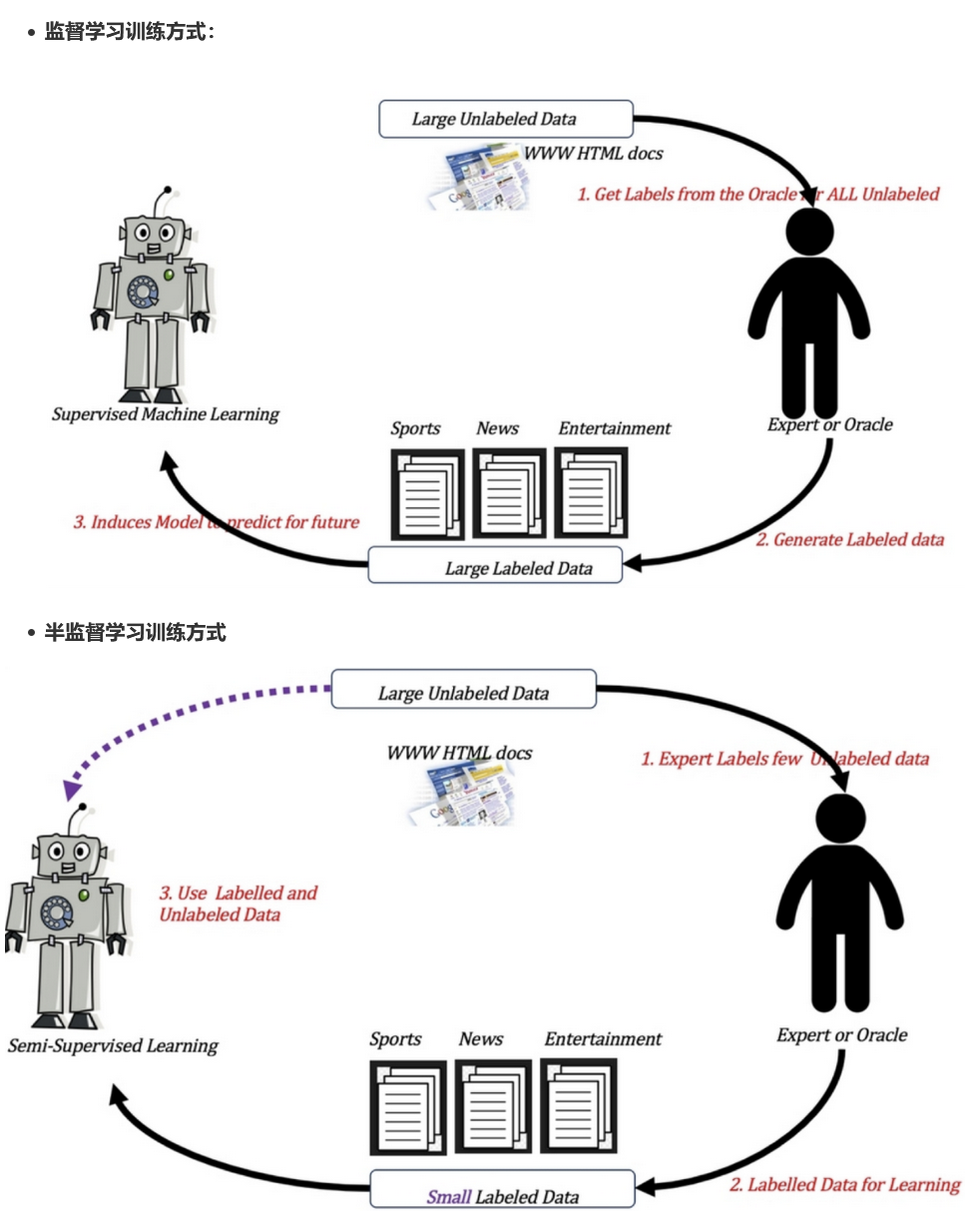
半监督学习
半监督学习: 训练集中有特征值,但是只有一部分数据有目标值,其他的没有目标值
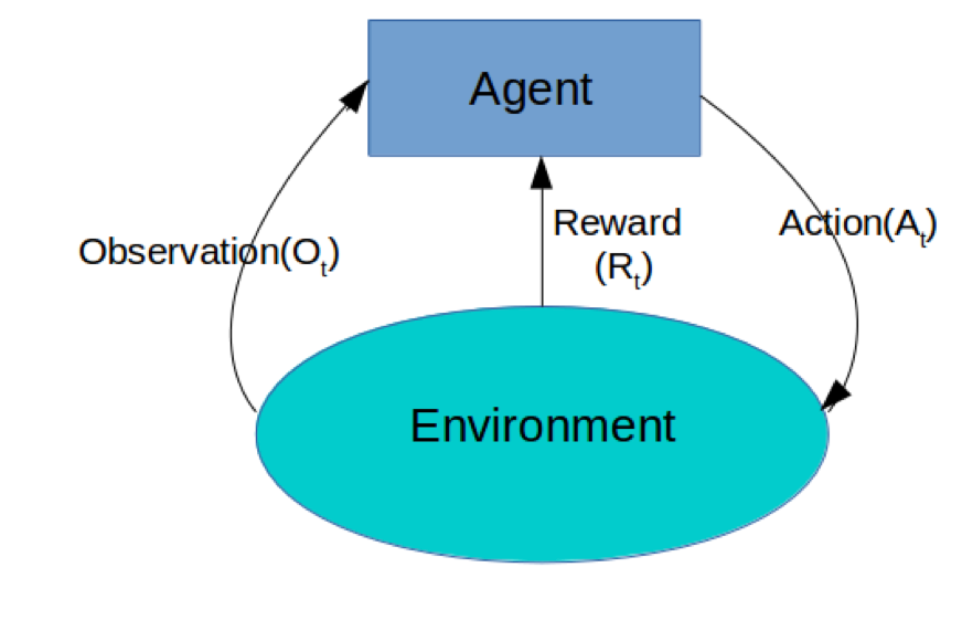
强化学习
强化学习: 本质是make decisions问题,即自动进行决策,并且可以做连续决策.
举例:
小孩想要走路,但在这之前,他需要先站起来,站起来之后还要保持平衡,接下来还要先迈出一条腿,是左腿还是右腿,迈出一步后还要迈出下一步 .
小孩就是agent,他试图通过采取行动action(即行走)来操作environment(行走的表面),并且从一个状态转变到另一个状态(即他走的每一步).
当他完成的子任务(即走了几步)时,孩子agent得到reward,并且当他不能走路时,不给reward.
主要包含四个元素: agent,environment,action,reward
监督学习和强化学习对比
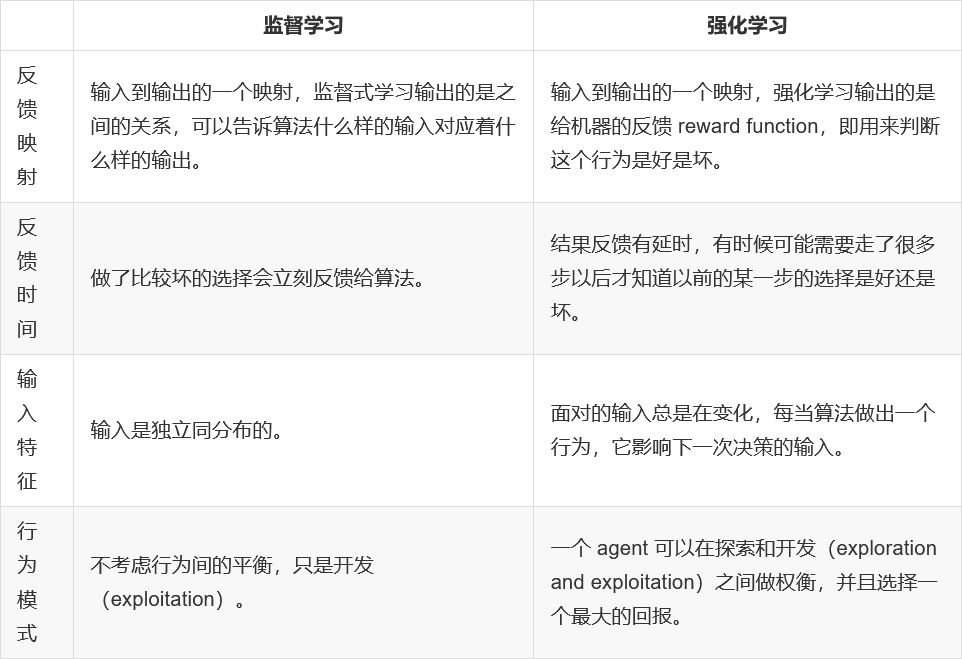
机器学习算法分类
监督学习: 有特征值,有目标值
回归问题: 目标值是连续的
分类问题: 目标值是离散的
无监督学习: 只有特征值
半监督学习: 有特征值,但是一部分数据有目标值,其他数据没有目标值
强化学习: 根据动态数据
模型评估
模型评估是模型开发过程中不可或缺的一部分.
它有助于发现表达数据的最佳模型和所选模型将来工作的性能如何.
按照数据集的目标值不同,可以把模型评估分为分类模型评估和回归模型评估.
分类模型评估
(1) 准确率: 预测正确的数占样本总数的比例
(2) 精确率: 正确预测为正占全部预测为正的比例.
(3) 召回率: 正确预测为正占全部正样本的比例.
(4) F1-score: 主要用于评估模型的稳健性.
(5) AUC指标: 主要用于评估样本不均衡的情况.
回归模型评估
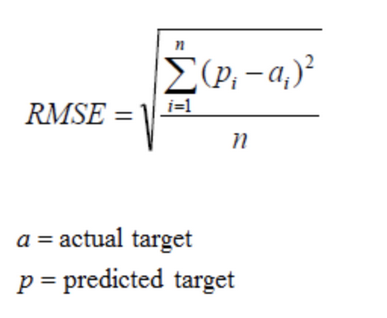
(1) 均方根误差(Root Mean Squared Error,RMSE)
RMSE是一个衡量回归误差率的常用公式,然而,它仅能比较误差是相同单位的模型.
(2) 相对平方误差(Relative Squared Error,RSE)
与RMSE不同,RSE可以比较误差是不同单位的模型.
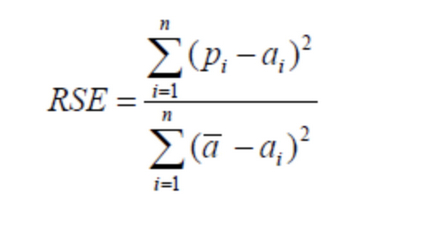
(3) 平均绝对误差(Mean Absolute Error,MAE)
MAE与原始数据单位相同, 它仅能比较误差是相同单位的模型。量级近似与RMSE,但是误差值相对小一些.
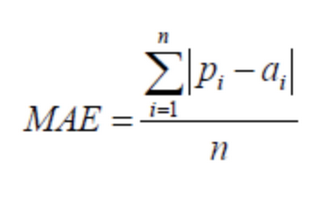
(4) 相对绝对误差(Relative Absolute Error,RAE)
与RSE不同,RAE可以比较误差是不同单位的模型
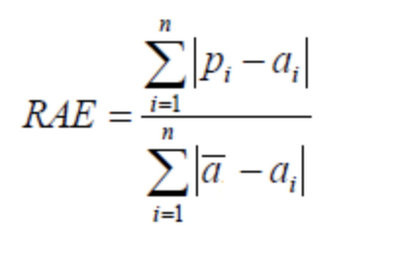
(5) 决定系数(Coefficient of Determination)
决定系数(R^2)回归模型汇总了回归模型的解释度,由平方和术语计算而得.

(R^2)描述了回归模型所解释的因变量方差在总方差中的比例.
(R^2)很大,即自变量和因变量之间存在线性关系,如果回归模型是"完美的",SSE为零,则(R^2)为1.
(R^2)小,则自变量和因变量之间存在线性关系的证据不令人信服.
如果回归魔I下那个完全失败,(SEE=SST),没有方差可被回归解释,则(R^2)为零.
拟合
模型评估用于评价训练好的模型的表现效果,其表现效果大致可以分为两类: 过拟合,欠拟合.
在训练过程中,你可能会遇到如下问题:
训练数据训练的很好啊,误差也不大,为什么在测试集上有问题呢?
当算法在某个数据集中出现了这种情况,可能就出现了拟合问题.
欠拟合
欠拟合: 学习到的特征太少.
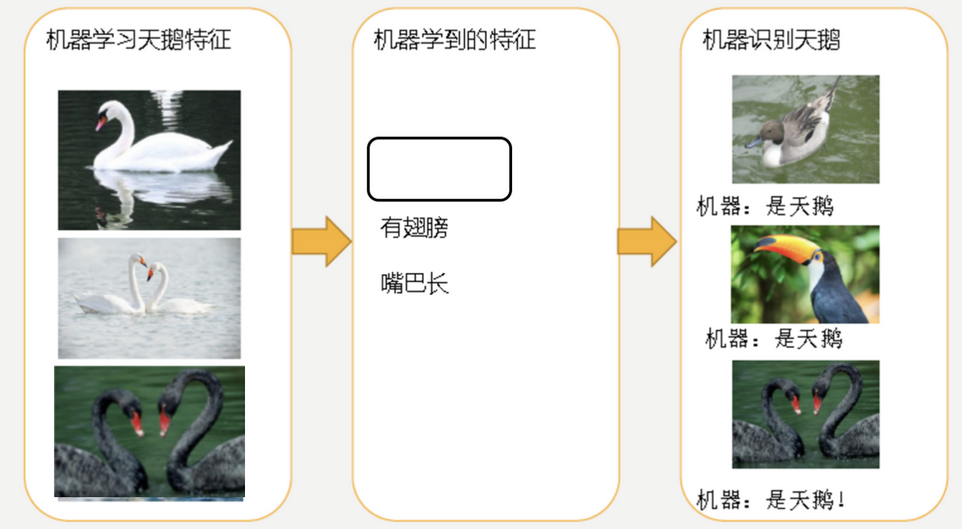
因为机器学习到的天鹅特征太少了,导致区分标准太粗糙,不能准确识别出天鹅.
过拟合
过拟合: 学习到的东西太多,不好泛化.
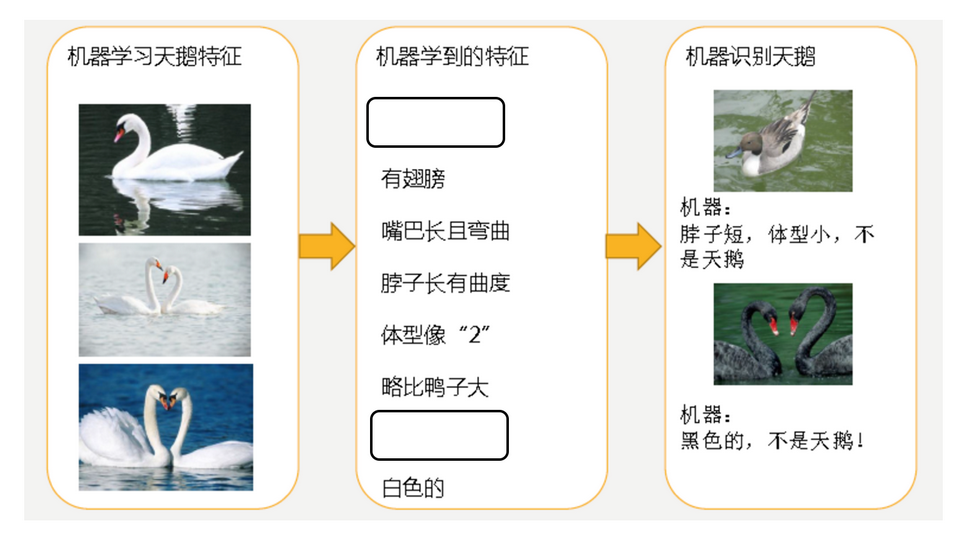
机器已经基本能区别天鹅和其他动物了.
但是,很不巧,已有的天鹅图片全是白天鹅的,于是机器经过学习后,会认为天鹅的羽毛都是白色的,以后看到羽毛是黑色的天鹅会任务那不是天鹅.
深度学习简介
深度学习 -- 神经网络简介
深度学习的发展源头 -- 神经网络.
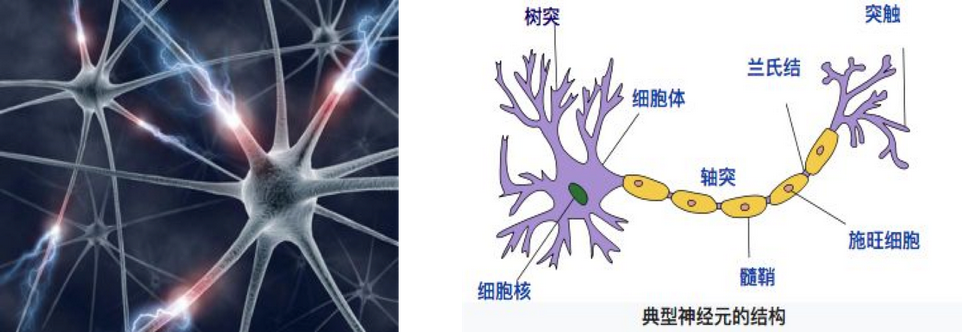
深度学习各层负责内容
