51nod 1197 字符串的数量 V2（矩阵快速幂+数论？）

　　接上一篇，那个递推式显然可以用矩阵快速幂优化...自己随便YY了下就出来了，学了一下怎么用LaTeX画公式，LaTeX真是个好东西！嘿嘿嘿

　　

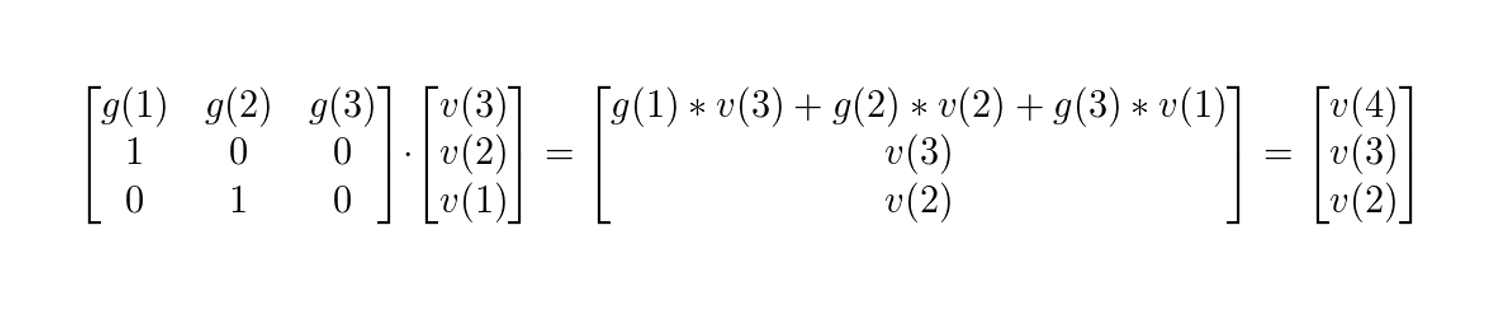
　　如上图。（刚画错了一发。。。已更新

　　然后就可以过V2了

　　orz CZL卡常大师，我怎么越卡越慢啊QAQ

#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#define ll long long 
using namespace std;
const int maxn=1000010,mod=1e9+7;
int n,m,k;
int sum[maxn],v[maxn],g[22],f[22][maxn];
void read(int &k)
{
    int f=1;k=0;char c=getchar();
    while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar();
    while(c<='9'&&c>='0')k=k*10+c-'0',c=getchar();
    k*=f;
}
int MOD(int x){return x>=mod?x-mod:x;}
int main()
{
    read(n);read(m);k=(int)floor(log(n)/log(2)+1);
    for(int i=1;i<=n;i++)f[1][i]=1,sum[i]=sum[i-1]+1;
    v[0]=1;g[1]=n-((n>>1)+1)+1;
    for(int i=2;i<=k;i++)
    {
        for(int j=1<<(i-1);j<=n;j++)f[i][j]=sum[j>>1];
        for(int j=(n>>1)+1;j<=n;j++)g[i]=MOD(g[i]+f[i][j]);
        sum[(1<<(i-1))-1]=0;for(int j=1<<(i-1);j<=n;j++)sum[j]=MOD(sum[j-1]+f[i][j]);
    }
    for(int i=1;i<=m;i++)
    {
        for(int j=1;j<=min(i,k);j++)
        v[i]=MOD(v[i]+(1ll*g[j]*v[i-j]%mod));
    }
    printf("%d
",v[m]);
    return 0;
}