考虑让总期望最小,那么就是期望经过次数越多的边贪心地给它越小的编号。
怎么求每条边的期望经过次数呢?边不大好算,我们考虑计算每个点的期望经过次数f[x],那么一条边的期望经过次数就是f[x]/d[x]+f[y]/d[y],d为度。
点的期望经过次数就很好算啦~
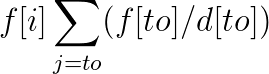
注意1一开始已经经过了1次,于是f[1]=sigma(f[to]/d[to)+1,到n之后就结束,所以到n的边的期望次数其实不由n决定,那直接把f[n]设为0,而且到n之后就结束,所有点是不能算从n来的边的,但是f[n]为0,所以就无所谓啦~
然后高斯消元,算出边的期望经过次数,期望经过次数越多的边贪心地给它越小的编号就好了。

#include<iostream> #include<cstring> #include<cstdlib> #include<cstdio> #include<cmath> #include<algorithm> #define ll long long using namespace std; const int maxn=510,maxm=500010,inf=1e9; struct poi{int too,pre;}e[maxm<<1]; int n,m,tot; int last[maxn],d[maxn],x[maxm],y[maxm]; double ans; double a[maxn][maxn],f[maxm]; void read(int &k) { int f=1;k=0;char c=getchar(); while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar(); while(c<='9'&&c>='0')k=k*10+c-'0',c=getchar(); k*=f; } void add(int x,int y){e[++tot].too=y;e[tot].pre=last[x];last[x]=tot;} bool gauss() { int to,now=1;double x; for(int i=1;i<=n;i++,now++) { for(to=now;to<=n;to++)if(fabs(a[to][i])>1e-8)break; if(to>n)continue; if(to!=now)for(int j=1;j<=n+1;j++)swap(a[now][j],a[to][j]); x=a[now][i];for(int j=1;j<=n+1;j++)a[now][j]/=x; for(int j=1;j<=n;j++) if(now!=j) { x=a[j][i]; for(int k=1;k<=n+1;k++)a[j][k]-=x*a[i][k]; } } for(int i=1;i<=n;i++)if(a[i][n+1]>1e-8)return 0; return 1; } int main() { read(n);read(m); for(int i=1;i<=m;i++) { read(x[i]),read(y[i]); add(x[i],y[i]);add(y[i],x[i]); d[x[i]]++;d[y[i]]++; } for(int i=1;i<n;i++) { a[i][i]=1.0; for(int j=last[i];j;j=e[j].pre) if(e[j].too!=n)a[i][e[j].too]=-1.0/d[e[j].too]; } a[1][n+1]=1.0;a[n][n]=1.0; gauss();for(int i=1;i<=m;i++)f[i]=a[x[i]][n+1]/d[x[i]]+a[y[i]][n+1]/d[y[i]]; sort(f+1,f+1+m); for(int i=1;i<=m;i++)ans+=f[i]*(m-i+1); printf("%.3lf ",ans); return 0; }
