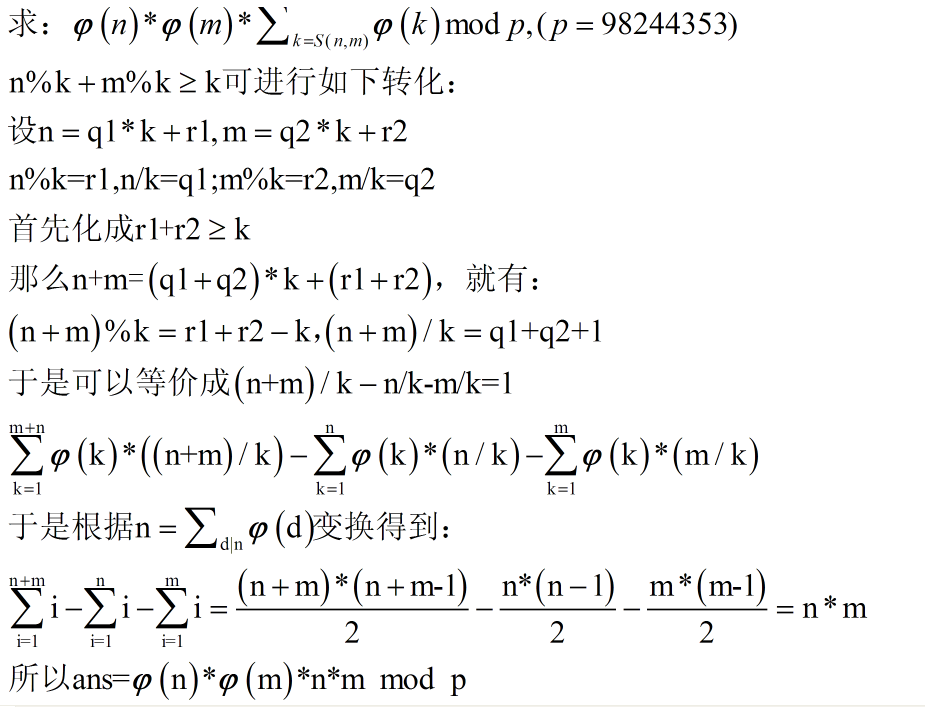同余

欧拉函数

计算欧拉函数(φ(n))（(1)~(n)于(n)互质的数的个数）

1. (φ(1)=1,φ(p)=p-1(mbox{p为素数}))
2. (φ(n)φ(m)=φ(nm))
3. 令(n=p_1^{a_1}p_2^{a_2}dots p_n^{a_n})，则有(φ(n)=n(1-p_1)(1-p_2)dots (1-p_n))

特性：(sum_{d|n}φ(d)=n)

例题：

1. BZOJ4173

   

   

#include<bits/stdc++.h>
#define MOD 998244353
using namespace std;
long long n,m;
long long Phi(long long n) {
    long long i,re=n;
    for(i=2;i*i<=n;i++) {    
        if(n%i==0) {
            re/=i;re*=i-1;
            while(n%i==0) {
                n/=i;
            }
        }    
    }
    if(n!=1) {
        re/=n,re*=n-1;
    }
    return re;
}
int main() {
    cin>>n>>m;
    cout<<(Phi(n)%MOD)*(Phi(m)%MOD)%MOD*(n%MOD)%MOD*(m%MOD)%MOD<<endl;
    return 0;
}

2. CF757E

   题目：https://blog.csdn.net/u010600261/article/details/54455941

   solution：https://blog.csdn.net/Feynman1999/article/details/82430887

   #include<bits/stdc++.h>
   #define N 1000010
   #define M 22
   #define mod 1000000007
   #define LL long long
   using namespace std;
   int m,f[N][M],p[N],pl,minp[N],ans,s[N][M];
   bool b[N];
   void get_p() {
   	for(int i=2; i<N; i++) {
   		if(b[i]==0) {
   			p[++pl]=i;
   			minp[i]=i;
   		}
   		for(int j=1; j<=pl; j++) {
   			if(i*p[j]>=N) break;
   			b[i*p[j]]=1;
   			minp[i*p[j]]=p[j];
   			if(i%p[j]==0) break;
   		}
   	}
   }
   int main() {
   	get_p();
   	for(int i=1; i<M; i++) f[0][i]=2,s[0][i]=2*i+1;
   	f[0][0]=s[0][0]=1;
   	for(int i=1; i<N; i++) {
   		for(int j=0; j<M; j++) {
   			f[i][j]=s[i-1][j];
   		}
   		s[i][0]=f[i][0];
   		for(int j=1; j<M; j++) {
   			s[i][j]=(s[i][j-1]+f[i][j])%mod;
   		}
   	}
   	scanf("%d",&m);
   	while(m--) {
   		int n,r;
   		scanf("%d%d",&r,&n);
   		ans=1;
   		while(n>1) {
   			int t=minp[n],k=0;
   			while(minp[n]==t) {
   				n/=t;
   				k++;
   			}
   			ans=(LL)ans*f[r][k]%mod;
   		}
   		printf("%d
   ",ans);
   	}
   	return 0;
   }
   

费马小定理

当(p)为质数且((a,p)=1)时，(a^{p-1}equiv1(mod: p))

显然费马小定理为欧拉定理的特例（(m)为质数）

Miller-Rabin算法

生成几个素数用费马小定理去测试这个数是否为素数（近似算法，有很小的几率判错）

和快速幂结合使用效果更佳

乘法逆元

若存在(x)使得(axequiv1(mod:m))，则称(x)为(a)的乘法逆元，记为(a^{-1}(mod: m))

求它的方法

1. 扩展欧几里得算法

   即求(ax+ny=1)

2. 欧拉定理

   求(a^{φ(n)-1}mod:m)即可

例题

SDOI 2016排列计数

中国剩余定理

例题：NOI2018屠龙勇士，P1495

源根

用途：快速数论变换（NTT）

补充

对于任意(n,min R)，如果有函数满足(f(n)f(m)=f(nm))，则称(f)函数为完全积性函数；同理如果(n,min Z^+)，则称(f)函数为积性函数。