一、基本概念
1.生成树
在一个V个点的无向连通图中,取v-1条边,并连接所有节点所得到的子图称为生成树
2.树的属性
(1)有v-1条边,无环
(2)有v-1条边,连通
(3)任意两个点之间只有唯一一条路径连接
(4)删除一条边后不连通
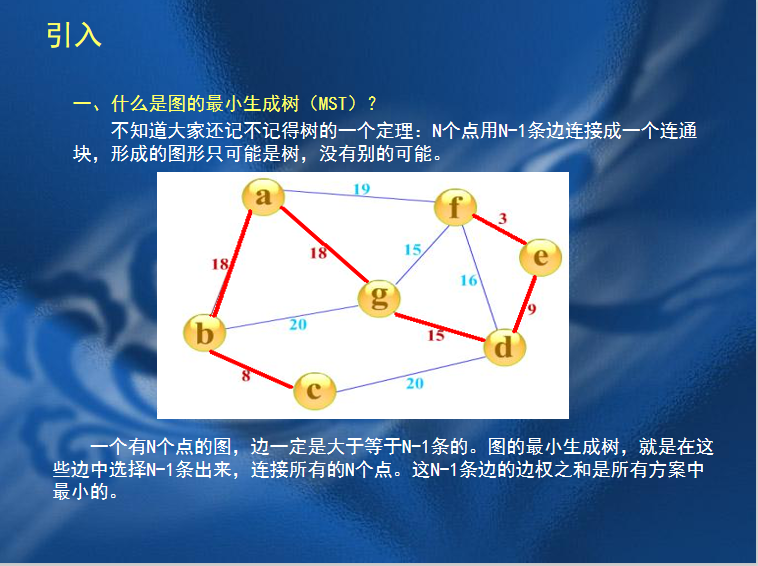
3.最小生成树
边权和最小的生成树
4.最小边原则
权值最小的边在最小生成树中
5.唯一性定理
对于图G,如果图中的边权值都不相同,则构成的最小生成树是唯一的
二、最小生成树算法
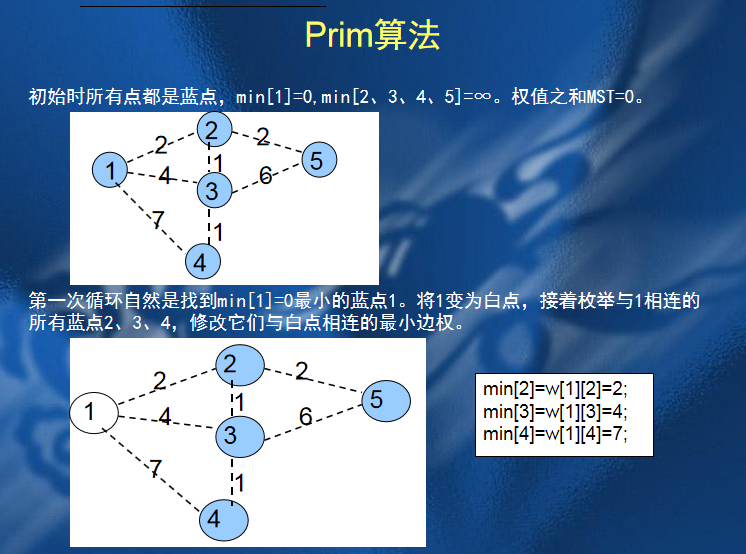
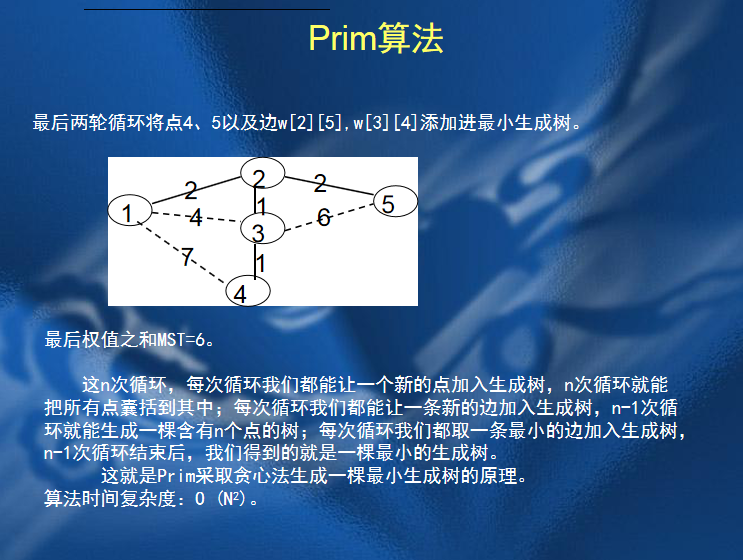
1.Prim算法




#include<cstdio> #include<queue> #include<cstring> #include<utility> #include<algorithm> #define FORa(i,s,e) for(i=s;i<=e;i++) #define R register int using namespace std; int n,m,cnt,ans,head[5005],dis[5005],bz[5005]; struct Edge { int next,to,dis; }edge[400005]; int num_edge; void Add_edge(int from,int to,int dis) { edge[++num_edge]=(Edge){head[from],to,dis}; head[from]=num_edge; } typedef pair <int,int> pp; priority_queue <pp,vector<pp>,greater<pp> > q;//first dis second u void Prim() { pp ft; dis[1]=0; q.push(make_pair(0,1)); while(!q.empty()&&cnt<n) { ft=q.top(),q.pop(); if(bz[ft.second]) continue; cnt++,ans+=ft.first,bz[ft.second]=1; for(R i=head[ft.second];i;i=edge[i].next) if(dis[edge[i].to]>edge[i].dis) dis[edge[i].to]=edge[i].dis,q.push(make_pair(dis[edge[i].to],edge[i].to)); } } int main() { memset(dis,127,sizeof(dis)); R from,to,fdis; scanf("%d%d",&n,&m); for(R i=1;i<=m;i++) { scanf("%d%d%d",&from,&to,&fdis); Add_edge(to,from,fdis),Add_edge(from,to,fdis); } Prim(); if (cnt==n)printf("%d",ans); else printf("orz"); }
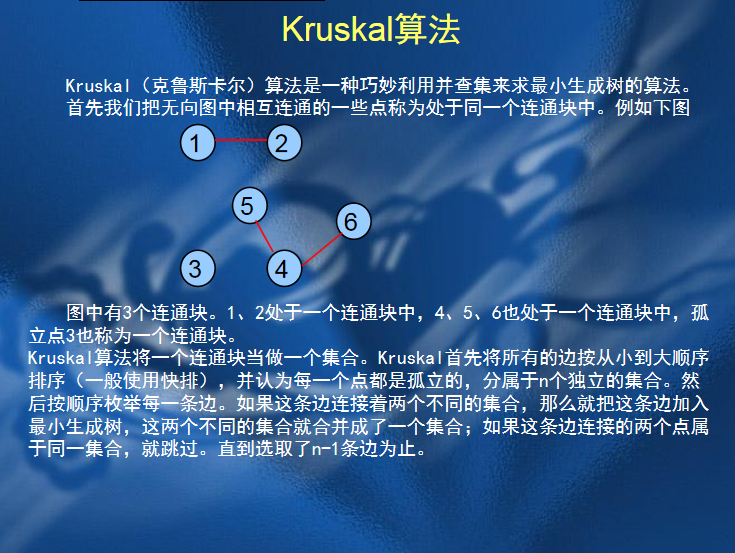
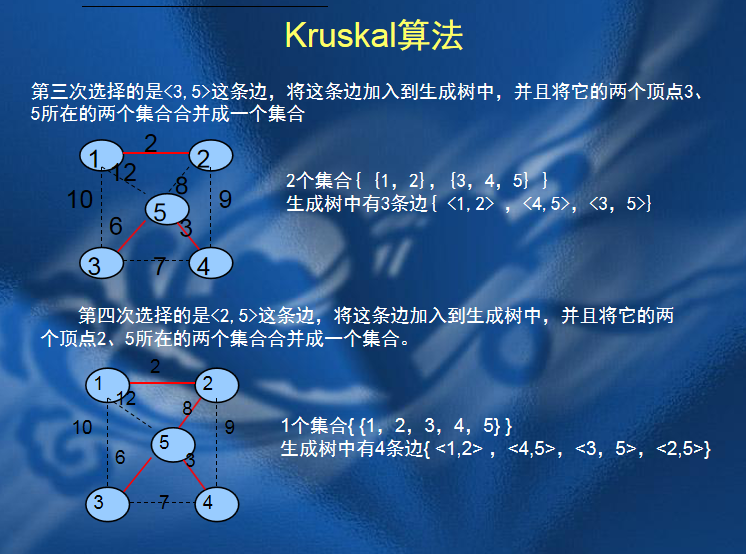
2.Kruskal算法




#include<stdio.h> #include<stdlib.h> #include<algorithm> #define LL long long #define FORa(i,s,e) for(int i=s;i<=e;i++) #define FORs(i,s,e) for(int i=s;i>=e;i--) using namespace std; const LL N=50000,M=200000; LL n,m,cnt,ans,num_edge,head[N+1],fa[N]; struct Edge{ LL next,from,to,dis; bool operator <(Edge &edge0)const { return dis<edge0.dis; } }edge[2*M+2]; void Add_edge(LL from,LL to,LL dis) { edge[++num_edge]=(Edge){head[from],from,to,dis}; head[from]=num_edge; } LL find(LL x) { while(fa[x]!=x) x=fa[x]=fa[fa[x]]; return x; } int main() { LL from,to,dis; scanf("%lld%lld",&n,&m); FORa(i,1,m) { scanf("%lld%lld%lld",&from,&to,&dis); Add_edge(from,to,dis); } FORa(i,1,n) fa[i]=i; sort(edge+1,edge+1+m); FORa(i,1,m) { LL t1=find(edge[i].from),t2=find(edge[i].to); if(t1!=t2) { fa[t1]=fa[t2],ans+=edge[i].dis,cnt++; if(cnt==n-1) break; } } if(cnt==n-1) printf("%lld",ans); else printf("orz"); return 0; }
