FJWC2018 - 走看看

泰迪每天都要通过一条路从家到学校，这条路的起点是泰迪家，终点则是学校。

这条路中间还有n个路口，从第i-1个路口走到第i个路口需要di秒，每个路口都有一个红绿灯。

更具体的，绿灯持续时间是g秒，红灯持续时间是r秒。

每天从第0秒开始，所有灯都是绿灯，持续g秒之后变为红灯，再过r秒变成绿灯，以此类推，并且同一时刻所有灯都是相同状态。

当泰迪到达一个路口，若是绿灯则可直接通过，若是红灯则需原地等待至绿灯。

若到达某一路口时灯的状态正好发生改变，则视达到路口时灯的颜色为其改变后的颜色，例如第g秒到达一个路口则视为遇到红灯。

现在泰迪预计了接下来q天从家出发的时间，第j天将会在第tj秒从家出发，他希望你告诉他每天到达学校的最早时间。

你可以假定一天内泰迪一定可以到达学校。

n, q ≤ 5 × 10^4 , 2 ≤ g, r ≤ 10^9 , di, tj ≤ 10^9

事实证明，半夜做题头是晕的、人是傻的。

一看这题，5e4，是两个log? 从此进入不归路……

先算前缀和，模g+r

写了个两个log的二分+主席树，主席树里面是权值线段树。

对于每个路口预处理在这里等到了绿灯之后，下一个碰到的红灯在哪里，从而算出在这个路口碰到红灯之后，还要走多久。

对于每个询问两个log算出第一个碰到的红灯。

其实可以一个log在主席树上二分的……

如果主席树里面是路口，外面是余数，那么对于一段区间的余数，我们就可以直接在主席树里面二分了。

询问也是同样。

再者，主席树也不需要，一颗线段树就足够了，线段数是按照余数建的，维护区间最小值(相当于最小路口的位置)。

我们肯定是从右到左预处理的，可以直接求余数在一段区间的路口的最小位置。

对于询问也是一样。

//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
#define lc son[pos][0]
#define rc son[pos][1]
const int maxn=5e6+7;
ll n,Q,G,R,mod,d[maxn],h[maxn],p[maxn],f[maxn],TOT,tot;
int next[maxn];
 
char cc; ll ff;
template<typename T>void read(T& aa) {
    aa=0;cc=getchar();ff=1;
    while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
    if(cc=='-') ff=-1,cc=getchar();
    while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
    aa*=ff;
}
 
int sum[maxn],son[maxn][2],ql,qr,qx;
void insert(int pos,int last,int l,int r) {
    sum[pos]=sum[last]+1;
    if(l==r) return;
    int mid=(l+r)>>1;
    if(qx<=mid) rc=son[last][1],insert(lc=++tot,son[last][0],l,mid);
    else lc=son[last][0],insert(rc=++tot,son[last][1],mid+1,r);
}
 
int q(int pos,int l,int r) {
    if((!pos)||ql>qr) return 0;
    if(l>=ql&&r<=qr) return sum[pos];
    int mid=(l+r)>>1,rs=0;
    if(ql<=mid) rs+=q(lc,l,mid);
    if(qr>mid) rs+=q(rc,mid+1,r);
    return rs;
}
 
bool ok(ll a,int pos,int x) {//(t+a)%mod>=g,(t+a)%mod<mod
    ll ld=(G+mod-a)%mod,rd=mod-a-1;
    if(ld<=rd) {
        ql=lower_bound(p+1,p+TOT+1,ld)-p; 
        qr=upper_bound(p+1,p+TOT+1,rd)-p-1;
        return (q(x,1,TOT)-q(pos,1,TOT))==0;
    }
    else {
        ql=1; qr=upper_bound(p+1,p+TOT+1,rd)-p-1;
        if((q(x,1,TOT)-q(pos,1,TOT))>0) return 0;
        ql=lower_bound(p+1,p+TOT+1,ld)-p; qr=TOT;//
        if((q(x,1,TOT)-q(pos,1,TOT))>0) return 0;
    }
    return 1;
}
 
bool check(int pos,int x) {//(0+t-h[pos])%mod>=g
    ll a=(mod-h[pos]%mod)%mod;
    return ok(a,pos,x);
}
 
int get_next(int p) {
    int l=p,r=n-1,mid;
    if(check(p-1,r)) return n+1;
    if(!check(p-1,l)) return l+1;
    while(l<r-1) {
        mid=(l+r)>>1;
        if(check(p-1,mid)) l=mid;
        else r=mid;
    }
    return l+2;
}
 
int ef(ll a) {
    int l=1,r=n-1,mid;
    if(ok(a,0,r)) return n+1;
    if(!ok(a,0,l)) return l+1;
    while(l<r-1) {
        mid=(l+r)>>1;
        if(ok(a,0,mid)) l=mid;
        else r=mid;
    }
    return l+2;
}
 
ll get_ans(ll x) {
    int pos=ef(x%mod);
    x+=h[pos-1];
    ll rs=x+f[pos];
    if(pos!=n+1) rs+=(mod-x%mod);
    return rs;
}
 
int main() {
    read(n); read(G); read(R); n++;
    ll x,y;
    mod=G+R;
    For(i,1,n) read(d[i]),h[i]=h[i-1]+d[i];
    For(i,1,n) p[i]=h[i]%mod;
    sort(p+1,p+n+1);
    TOT=unique(p+1,p+n+1)-(p+1);
    tot=n;
    For(i,1,n) {
        qx=lower_bound(p+1,p+TOT+1,h[i]%mod)-p;
        insert(i,i-1,1,TOT);
    }
    next[n]=n+1;
    Rep(i,n,1) next[i]=get_next(i);
    Rep(i,n,1) {
        x=h[next[i]-1]-h[i-1];
        f[i]=f[next[i]]+x;
        if(next[i]!=n+1) f[i]+=(mod-x%mod);
    }
    read(Q);
    For(i,1,Q) {
        read(x);
        printf("%lld
",get_ans(x));
    }
    return 0;
}

敲完这道题，键盘坏了，心态崩了

只能看一看其他题了

第二天上午测试，11点的时候写完了Day1，就来做T2吧

bzoj5255全排列

定义两个长为n的排列A与B相似：若?i，满足C(A, Ai) = C(B, Bi)。其中C(P, x)为满足Pj < x(1 ≤ j ≤ n)的j的数目。

对于两个常委n的排列P1,P2，定义函数F(P1,P2)等于满足P1[l . . . r] 相似于P2[l . . . r](1 ≤ l ≤r ≤ n)并且P1[l . . . r]包含不超过E个逆序对的数对(l,r)的数目。

现在请你求出：对P1,P2分别取遍所有1~n的排列后所有F(P1,P2)的和

T ≤ 10^4, n ≤ 500, E ≤ 10^6

先预处理f[i][j]表示1~i的全排列中逆序对数是j的全排列个数，算了一下空间，刚刚够。

转移的时候，差分前缀和优化一下。

然后算f[i][j]表示1~i的全排列中逆序对数小于等于j的全排列个数。

预处理组合数的平方。

对于询问，枚举子串长度，组合排列算方案。

没卡常，T了，随便卡卡常，过了。

//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(register int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(register int i=(a);i>=(b);--i)
const int maxn=500+3,maxt=250*499+3,maxT=1e4+7;
const ll mod=1e9+7;
ll Td,n[maxT],m[maxT],f[maxn][maxt],mi[maxn],inv[maxn],C[maxn][maxn],W;

char cc; ll ff;
template<typename T>void read(T& aa) {
	aa=0;cc=getchar();ff=1;
	while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
	if(cc=='-') ff=-1,cc=getchar();
	while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
	aa*=ff;
}

ll qp(ll x,ll k) {
	ll rs=1;
	while(k) {
		if(k&1) rs=rs*x%mod;
		k>>=1; x=x*x%mod;
	}
	return rs;
}

ll get_C(ll n,ll m) {return mi[n]*inv[m]%mod*inv[n-m]%mod;}
inline void mo(ll& x) {if(x>=mod) x-=mod;}
ll pf(ll x){return x*x%mod;}

ll solve(ll n,ll m) {
	ll rs=0,x;
	For(i,1,n) {//len=i
		x=min(m,(ll)i*(i-1)/2);
		rs+=C[n][i]*(n-i+1)%mod*mi[n-i]%mod*f[i][x]%mod;
		mo(rs);
	}
	return rs;
}

int main() {
	read(Td);ll x;
	For(i,1,Td) {
		read(n[i]); read(m[i]);
		W=max(W,n[i]);
	}
	mi[0]=1; For(i,1,W) mi[i]=mi[i-1]*i%mod;
	inv[W]=qp(mi[W],mod-2);
	Rep(i,W,1) inv[i-1]=inv[i]*i%mod;
	f[0][0]=1;
//	cerr<<clock()<<"
";
	For(i,0,W-1) {
		x=i*(i-1)/2;
		For(j,0,x) {
			f[i][j]+=f[i][j-1]; f[i][j]%=mod;
			//f[i+1][j+0~j+i] += f[i][j]
			f[i+1][j]+=f[i][j];
			f[i+1][j+i+1]+=mod-f[i][j];
		}
	}
	x=W*(W-1)/2;
	For(j,0,x) f[W][j]+=f[W][j-1],mo(f[W][j]);
//	cerr<<clock()<<"
";
	//f[i][j]: perm of 1~i , inverse:j
	For(i,0,W) {
		x=i*(i-1)/2;
		For(j,1,x) {
			f[i][j]+=f[i][j-1]; mo(f[i][j]);
		}
	}
//	cerr<<clock()<<"
";
	//f[i][j]: perm of 1~i , inverse:0~j 
	For(i,1,W) For(j,0,i) C[i][j]=pf(get_C(i,j));
	For(i,1,W) mi[i]=pf(mi[i]);
	For(i,1,Td) 
		printf("%lld
",solve(n[i],m[i]));
	return 0;
}

bzoj5256井井点点

在一个二维平面上有一个图形，如下图所示：

###############
#.............#
#.###########.#
#.#.........#.#
#.#.#######.#.#
#.#.#.....#.#.#
#.#.#.###.#.#.#
#.#.#.#.#.#.#.#
#.#.#.###.#.#.#
#.#.#.....#.#.#
#.#.#######.#.#
#.#.........#.#
#.###########.#
#.............#
###############

它是一个中心为一个字符'.'，之后按照一层'#'一层'.'的顺序围起来的无限大的图形。

现在给定若干个位置上的字符，请你确定出这个图形中心位置的坐标，若有多个合法中心位置，

则输出离原点曼哈顿距离最近的一个。若仍有多个，则输出横坐标最大的一个，

若还有多个，输出纵坐标最大的一个；若没有合法中心点，输出"Too damaged".

n ≤ 1000, |x|, |y| ≤ 10^15, T ≤ 50 , c ∈ {., #}

不信邪又在半夜做题……

这道题好难呀，这道题为什么这么难呀，我做不起呀……

“

若有多个合法中心位置，

则输出离原点曼哈顿距离最近的一个。若仍有多个，则输出横坐标最大的一个，

若还有多个，输出纵坐标最大的一个；若没有合法中心点，输出"Too damaged".

“

而且还这么麻烦。

算了算了先试试推一推再说

如果中心在$(x_0,y_0)$，一个在$(x,y)$的点，是'.'还是'#'和 $ max( abs(x-x_0) , abs(y-y_0) ) &1 $ 有关

枚举$x_0$和$y_0$的奇偶，如果合法，对于一个点$(x,y)$，有三种情况：

1、不能出现$abs(x-x_0) > abs(y-y_0)$

2、不能出现$abs(y-y_0) > abs(x-x_0)$

3、$abs(x-x_0)$和$abs(y-y_0)$大小关系无所谓

这不是一个十字叉叉的图形嘛：

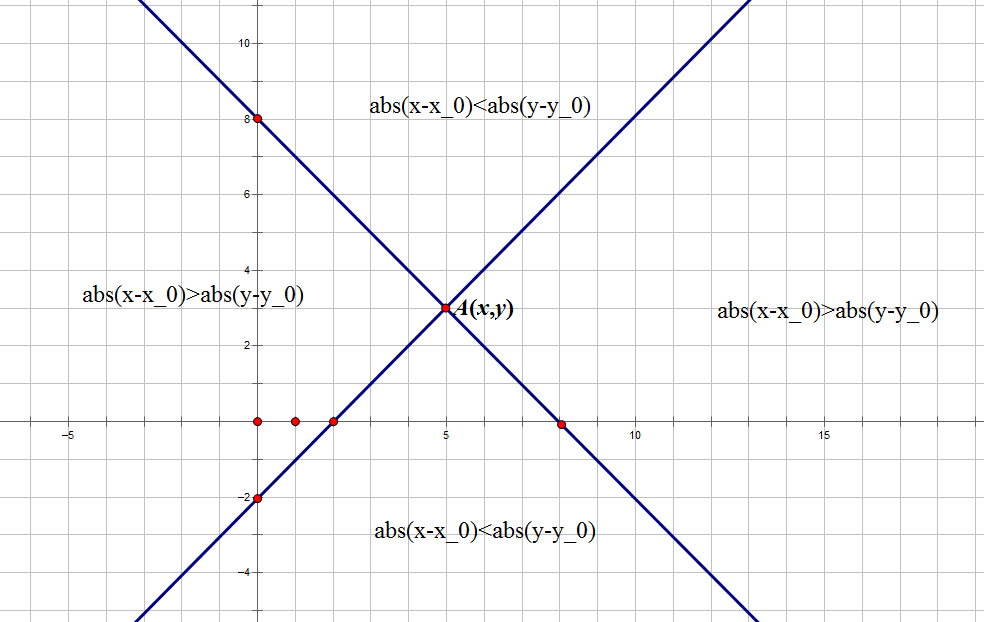
这玩意要求交或者求并？

那就拆成两条线，一条是x+y=A，一条是y-x=B，分别求最大最小的4条线？

噼里啪啦打完啦，怎么样例都调不过呀，woc我写了个假算法……

搜搜题解吧，哇，这道题怎么连题解都没有，心态崩了，睡了睡了。

这天晚上，我做了一个梦，梦中有人说：你怎么这么傻呀，这道题怎么可能是Tn的算法呢，肯定有个log或者根号一类的呀。

旋转坐标系，一个点把平面分成左上、左下、右上、右下四部分。

分别把四部分做一个排序后单调栈，枚举出现的过的横坐标或者纵坐标，在单调栈里面二分求出可行的区间，再判断？

怎么这么难打呀，我是不是又把问题想复杂了呀，为什么别人的AC代码只有2k、3k呀。

不敢下手呀，还是再想想其他方法吧。