整数划分问题是算法中的一个经典命题之一,有关这个问题的讲述在讲解到递归时基本都将涉及。所谓整数划分,是指把一个正整数n写成如下形式:n=m1+m2+...+mi; (其中mi为正整数,并且1 <= mi <= n),则{m1,m2,...,mi}为n的一个划分。如果{m1,m2,...,mi}中的最大值不超过m,即max(m1,m2,...,mi)<=m,则称它属于n的一个m划分。这里我们记n的m划分的个数为f(n,m);例如但n=4时,他有5个划分,{4},{3,1},{2,2},{2,1,1},{1,1,1,1};注意4=1+3 和 4=3+1被认为是同一个划分。该问题是求出n的所有划分个数,即f(n, n)。
下面我们考虑求f(n,m)的方法;
———————————————————————————华丽的分割线———————————————————————————
(一)递归法
根据n和m的关系,考虑以下几种情况:
(1)当n=1时,不论m的值为多少(m>0),只有一种划分即{1};
(2) 当m=1时,不论n的值为多少,只有一种划分即n个1,{1,1,1,...,1};
(3) 当n=m时,根据划分中是否包含n,可以分为两种情况:
(a). 划分中包含n的情况,只有一个即{n};
(b). 划分中不包含n的情况,这时划分中最大的数字也一定比n小,即n的所有(n-1)划分。
因此 f(n,n) =1 + f(n,n-1);
(4) 当n<m时,由于划分中不可能出现负数,因此就相当于f(n,n);
(5) 但n>m时,根据划分中是否包含最大值m,可以分为两种情况:
(a). 划分中包含m的情况,即{m, {x1,x2,...xi}}, 其中{x1,x2,... xi} 的和为n-m,可能再次出现m,因此是(n-m)的m划分,因此这种划分
个数为f(n-m, m);
(b). 划分中不包含m的情况,则划分中所有值都比m小,即n的(m-1)划分,个数为f(n,m-1);
因此 f(n, m) = f(n-m, m)+f(n,m-1);
综合以上情况,我们可以看出,上面的结论具有递归定义特征,其中(1)和(2)属于回归条件,(3)和(4)属于特殊情况,将会转换为情况(5)。而情况(5)为通用情况,属于递推的方法,其本质主要是通过减小m以达到回归条件,从而解决问题。其递推表达式如下:
f(n, m)= 1; (n=1 or m=1)
f(n, n); (n<m)
1+ f(n, m-1); (n=m)
f(n-m,m)+f(n,m-1); (n>m)
因此我们可以给出求出f(n, m)的递归函数代码如下(引用Copyright Ching-Kuang Shene July/23/1989的代码):

1 计算f(n,m),即n的m划分的个数 2 unsigned long GetPartitionCount(int n, int max) 3 { 4 if (n == 1 || max == 1) 5 return 1; 6 else if (n < max) 7 return compute(n, n); 8 else if (n == max) 9 return 1 + GetPartitionCount(n, max-1); 10 else 11 return GetPartitionCount(n,max-1) + GetPartitionCount(n-max, max); 12 }
我们可以发现,这个命题的特征和另一个递归命题:
“上台阶”问题(斐波那契数列)(http://www.cnblogs.com/hoodlum1980/archive/2007/07/13/817188.html)
相似,也就是说,由于树的“天然递归性”,使这类问题的解可以通过树来展现,每一个叶子节点的路径是一个解。因此把上面的函数改造一下,让所有划分装配到一个.NET类库中的TreeView控件,相关代码(c#)如下:

1 组装TreeView 2 /// <param name="root">树的根结点</param> 3 /// <param name="n">被划分的整数</param> 4 /// <param name="max">一个划分中的最大数</param> 5 /// <returns>返回划分数,即叶子节点数</returns> 6 private int BuildPartitionTree(TreeNode root, int n, int max) 7 { 8 int count=0; 9 if( n==1) 10 { 11 //{n}即1个n 12 root.Nodes.Add(n.ToString());//{n} 13 return 1; 14 } 15 else if( max==1) 16 { 17 //{1,1,1,,1} 即n个1 18 TreeNode lastNode=root; 19 or(int j=0; j<n; j++) 20 21 { 22 lastNode.Nodes.Add("1"); 23 lastNode=lastNode.LastNode; 24 } 25 return 1; 26 } 27 else if(n<max) 28 { 29 return BuildPartitionTree(root, n, n); 30 } 31 else if(n==max) 32 { 33 root.Nodes.Add(n.ToString()); //{n} 34 count=BuildPartitionTree(root, n, max-1); 35 return count+1; 36 } 37 else 38 { 39 //包含max的分割,{max, {n-max}} 40 TreeNode node=new TreeNode(max.ToString()); 41 root.Nodes.Add(node); 42 count += BuildPartitionTree(node, n-max, max); 43 44 //不包含max的分割,即所有max-1分割 45 count += BuildPartitionTree(root, n, max-1); 46 return count; 47 } 48 }
如果我们要输出所有解,只需要输出所有叶子节点的路径即可,可以同样用递归函数来输出所有叶子节点(代码中使用了一个StringBuilder对象来接收所有叶子节点的路径):

1 获取所有叶子节点的路径 2 private void PrintAllLeafPaths(TreeNode node) 3 { 4 //属于叶子节点? 5 if(node.Nodes.Count==0) 6 this.m_AllPartitions.AppendFormat("{0} ", node.FullPath.Replace('\',',')); 7 else 8 { 9 foreach(TreeNode child in node.Nodes) 10 { 11 this.PrintAllLeafPaths(child); 12 } 13 } 14 }
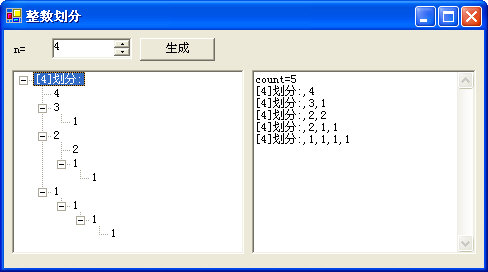
通过递归思路,我们给出了n的划分个数的算法,也把所有划分组装到一棵树中。好,关于递归思路我们就暂时介绍到这里。关于输出所有划分的标准代码在这里省略了,我们有时间再做详细分析。
———————————————————————————华丽的分割线———————————————————————————
(二)母函数法
下面我们从另一个角度即“母函数”的角度来考虑这个问题。
所谓母函数,即为关于x的一个多项式G(x):
有 G(x)= a0 + a1*x + a2*x^2 + a3*x^3 + ...
则我们称G(x)为序列(a0,a1,a2,...)的母函数。关于母函数的思路我们不做更多分析。
我们从整数划分考虑,假设n的某个划分中,1的出现个数记为a1,2的个数记为a2,..., i的个数记为ai,
显然: ak<=n/k; (0<= k <=n)
因此n的划分数f(n,n),也就是从1到n这n个数字中抽取这样的组合,每个数字理论上可以无限重复出现,即个数随意,使他们的总和为n。显然,数字i可以有如下可能,出现0次(即不出现),1次,2次,..., k次,等等。把数字i用(x^i)表示,出现k次的数字i用 x^(i*k)表示, 不出现用1表示。例如数字2用x^2表示,2个2用x^4表示,3个2用x^6表示,k个2用x^2k表示。
则对于从1到N的所有可能组合结果我们可以表示为:
G(x) = (1+x+x^2+x^3+...+x^n) (1+x^2+x^4+...) (1+x^3+x^6+...) ... (1+x^n)
= g(x,1) g(x,2) g(x,3) ... g(x, n)
= a0 + a1* x + a2* x^2 + ... + an* x^n + ... ; (展开式)
上面的表达式中,每一个括号内的多项式代表了数字i的参与到划分中的所有可能情况。因此该多项式展开后,由于x^a * x^b=x^(a+b),因此 x^i 就代表了i的划分,展开后(x^i)项的系数也就是i的所有划分的个数,即f(n,n)=an (上式中g(x,i)表示数字i的所有可能出现情况)。
由此我们找到了关于整数划分的母函数G(x);剩下的问题是,我们需要求出G(x)的展开后的所有系数。
为此我们首先要做多项式乘法,对于我们来说并不困难。我们把一个关于x的一元多项式用一个整数数组a[]表示,a[i]代表x^i的系数,即:
g(x) = a[0] + a[1]x + a[2]x^2 + ... + a[n]x^n;
则关于多项式乘法的代码如下,其中数组a和数组b表示两个要相乘的多项式,结果存储到数组c:

1 多项式相乘,即c=a*b 2 #define N 130 3 unsigned long a[N];/*多项式a的系数数组*/ 4 unsigned long b[N];/*多项式b的系数数组*/ 5 unsigned long c[N];/*存储多项式a*b的结果*/ 6 /*两个多项式进行乘法,系数分别在a和b中,结果保存到c ,项最大次数到N */ 7 /*注意这里我们只需要计算到前N项就够了。*/ 8 void Poly() 9 { 10 int i,j; 11 memset(c,0,sizeof(c)); 12 for(i=0; i<N; i++) 13 for(j=0; j<N-i; j++) /*y<N-i: 确保i+j不会越界*/ 14 c[i+j] += a[i]*b[j]; 15 }
下面我们求出G(x)的展开结果,G(x)是n个多项式连乘的结果:

1 计算G(x)的前N项系数 2 /*计算出前N项系数!即g(x,1) g(x,2)... g(x,n)的展开结果*/ 3 void Init() 4 { 5 int i,k; 6 memset(a,0,sizeof(a)); 7 memset(c,0,sizeof(c)); 8 for(i=0; i<N; i++) a[i]=1; /*第一个多项式:g(x, 1) = x^0 + x^1 + x^2 + x^3 + */ 9 for(k=2; k<N; k++) 10 { 11 memset(b,0,sizeof(b)); 12 for(i=0; i<N; i+=k) b[i]=1; /*第k个多项式:g(x, k) = x^0 + x^(k) + x^(2k) + x^(3k) + */ 13 Poly(); /* 多项式乘法:c= a*b */ 14 memcpy(a,c,sizeof(c)); /*把相乘的结果从c复制到a中:c=a; */ 15 } 16 }
通过以上的代码,我们就计算出了G(x)的展开后的结果,保存到数组c中。此时有:f(n,n)=c[n];剩下的工作只是把相应的数组元素输出即可。
问题到了这里已经解决完毕。但我们发现,针对该问题,g(x,k)是一个比较特殊的多项式,特点是只有k的整数倍的索引位置有项,而其他位置都为0,具有项“稀疏”的特点,并且项次分布均匀(次数跨度为k)。这样我们就可以考虑在计算多项式乘法时,可以减少一些循环。因此可以对Poly函数做这样的一个改进,即把k作为参数传递给Poly:

1 改进后的多项式乘法 2 /*两个多项式进行乘法,系数分别在a和b中,结果保存到c ,项最大次数到N */ 3 /*改进后,多项式a乘以一个有特殊规律的多项式b,即b中只含有x^(k*i)项,i=0,1,2,*/ 4 /*如果b没有规律,只需要把k设为1,即与原来函数等效*/ 5 void Poly2(int k) /*参数k的含义:表示b中只有b[k*i]不为0!*/ 6 { 7 int i,j; 8 memset(c,0,sizeof(c)); 9 for(i=0; i<N; i++) 10 for(j=0; j<N-i; j+=k) 11 c[i+j] += a[i]*b[j]; 12 }
这样,原有的函数可以认为是k=1的情况(即多项式b不具有上诉规律)。相应的,在上面的Init函数中的调用改为Poly2(k)即可。
———————————————————————————————————————————————————————————
参考资料:
(1)关于“递归”部分的代码,参考了Ching-Kuang Shene,July/23/1989的代码;
(2)关于“母函数”部分,参考了《Acm程序设计》(刘春英)(PPT文档);
(3)“母函数”方法的Init和Poly的代码,参考了某位教师的代码 : ymc 2008/09/25, 其中多项式乘法的改进是我提出的建议。
-- by hoodlum1980 2008-10-11
练习:
整数划分问题
每组输入是两个整数n和k。(1 <= n <= 50, 1 <= k <= n)
Output
对于每组输入,请输出六行。
第一行: 将n划分成若干正整数之和的划分数。
Sample Input
Sample Output
Hint:

1 # include <stdio.h> 2 #define N 100 3 int a[N],b[N],c[N],d[N],e[N]; 4 int t=0,total=0,count=0; 5 int n,p=0; 6 7 int dif() 8 { 9 int i,j; 10 for(i=0; i<t-1; i++) 11 for(j=i+1; j<t; j++) 12 if(e[i]==e[j]) return 0; 13 return 1; 14 } 15 16 void fun() 17 { 18 t=0; 19 total=0; 20 count=0; 21 } 22 void fun1(int x) // 将n划分成若干正整数之和的划分数。 23 { 24 int i,j; 25 if(total==n) 26 { 27 count++; 28 printf("%d=",n); 29 for(j=0; j<t; j++) 30 { 31 printf("%d",a[j]); 32 if(j<t-1) printf("+"); 33 else 34 { 35 if(n-a[0]==t-1) printf(" "); 36 else printf(","); 37 } 38 } 39 } 40 else 41 for(i=x; i>=1; i--) 42 if(i+total<=n) 43 { 44 a[t++]=i; 45 total+=i; 46 fun1(i); 47 } 48 total-=a[t-1]; 49 t--; 50 } 51 52 void fun2(int x,int m) //将n划分成k个正整数之和的划分数。 53 { 54 int i,j; 55 if(total==n) 56 { 57 if(p==m) 58 { 59 count++; 60 printf("%d=",n); 61 for(j=0; j<t; j++) 62 { 63 printf("%d",b[j]); 64 if(j<t-1) printf("+"); 65 else printf(" "); 66 } 67 } 68 } 69 else 70 for(i=x; i>=1; i--) 71 if(i+total<=n) 72 { 73 b[t++]=i; 74 p++; 75 total+=i; 76 fun2(i,m); 77 } 78 total-=b[t-1]; 79 t--; 80 p--; 81 } 82 83 void fun3(int x,int m) //将n划分成最大数不超过k的划分数。 84 { 85 int i,j; 86 if(total==n) 87 { 88 count++; 89 printf("%d=",n); 90 for(j=0; j<t; j++) 91 { 92 printf("%d",c[j]); 93 if(j<t-1) printf("+"); 94 else 95 { 96 if(n-c[0]==t-1) printf(" "); 97 else printf(","); 98 } 99 } 100 } 101 else 102 for(i=m; i>=1; i--) 103 if(i+total<=n) 104 { 105 c[t++]=i; 106 total+=i; 107 fun3(i,m); 108 } 109 total-=c[t-1]; 110 t--; 111 } 112 113 void fun4(int x) //将n划分成若干奇正整数之和的划分数。 114 { 115 int i,j; 116 if(total==n) 117 { 118 count++; 119 printf("%d=",n); 120 for(j=0; j<t; j++) 121 { 122 printf("%d",d[j]); 123 if(j<t-1) printf("+"); 124 else 125 { 126 if(n-d[0]==t-1) printf(" "); 127 else printf(","); 128 } 129 } 130 } 131 else 132 for(i=x; i>=1; i--) 133 if(i+total<=n&&i%2!=0) 134 { 135 d[t++]=i; 136 total+=i; 137 fun4(i); 138 } 139 total-=d[t-1]; 140 t--; 141 } 142 143 void fun5(int x) //将n划分成若干不同整数之和的划分数。 144 { 145 int i,j; 146 if(total==n) 147 { 148 if(dif()) 149 { 150 count++; 151 printf("%d=",n); 152 for(j=0; j<t; j++) 153 { 154 printf("%d",e[j]); 155 if(j<t-1) printf("+"); 156 else printf(" "); 157 } 158 } 159 } 160 else 161 for(i=x; i>=1; i--) 162 if(i+total<=n) 163 { 164 e[t++]=i; 165 total+=i; 166 fun5(i); 167 } 168 total-=e[t-1]; 169 t--; 170 } 171 int main() 172 { 173 int k; 174 printf("输入是两个整数n和k。(1 <= n <= 50, 1 <= k <= n):"); 175 scanf("%d%d",&n,&k); 176 fun1(n);// 将n划分成若干正整数之和的划分数。 177 printf("将%d划分成若干正整数之和的划分数:%d ",n,count); 178 179 fun(); 180 fun2(n,k);//将n划分成k个正整数之和的划分数。 181 printf(" 将%d划分成%d个正整数之和的划分数:%d ",n,k,count); 182 183 fun(); 184 fun3(n,k);//将n划分成最大数不超过k的划分数。 185 printf("将%d划分成最大数不超过%d的划分数:%d ",n,k,count); 186 187 fun(); 188 fun4(n);//将n划分成若干奇正整数之和的划分数。 189 printf("将%d划分成若干奇正整数之和的划分数:%d ",n,count); 190 191 fun(); 192 fun5(n);//将n划分成若干不同整数之和的划分数。 193 printf("将%d划分成若干不同整数之和的划分数:%d ",n,count); 194 195 return 0; 196 }
