写在前面
貌似是一个比较冷门的算法?还是说我见识少?
不过不管怎样,既然 CCF 的 NOI 大纲里出了,就把这个知识点补上吧。
原理
笛卡尔树是一个二叉树,每一个结点有一个键值二元组 ((k,w)) 组成(就是一个点同时带着两个信息,一般好像是下标 (k) 和权值 (w))
它要求 (k) 满足二叉搜索树的性质,(w) 满足堆的性质。
举个 OI-Wiki 上的例子
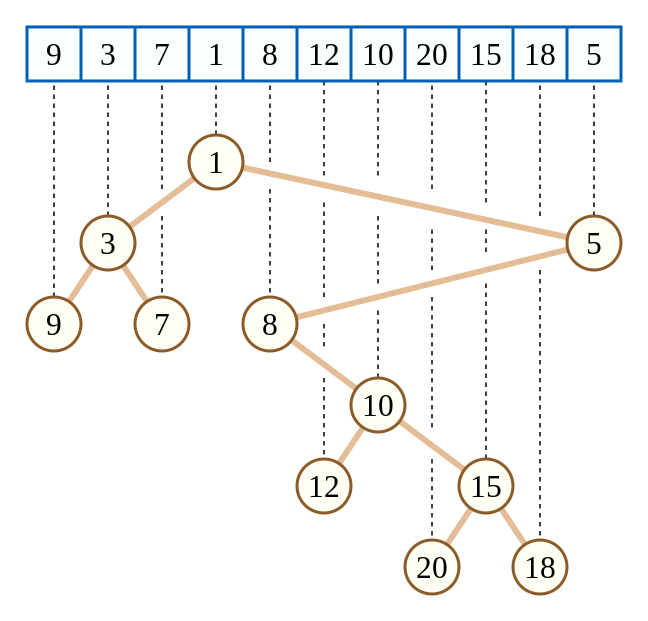
这张图把序列的下标当做 (k),元素的值当做 (w)。
不难发现,每个元素所对应的下标在树上满足二叉搜索树的性质;
每个元素的权值也恰好构成了一个小根堆。
构建
一种常见的方法是栈构建。
首先按键值 (k) 排序(上面那课笛卡尔树的键值是下标,所以不用排序)。
用单调栈维护这个树的右链。
每次插入 (u) 执行这样一个过程:
从下到上遍历,比较键值 (w) 的大小,找到一个结点 (x) ,满足 (x_w < u_w),然后把 (u) 接到 (x) 的右儿子上,(x) 原本的右子树变为 (x) 的左子树。
再给一张 OI-Wiki 的图,红色框内是我们维护的右链,应该比较清晰了。
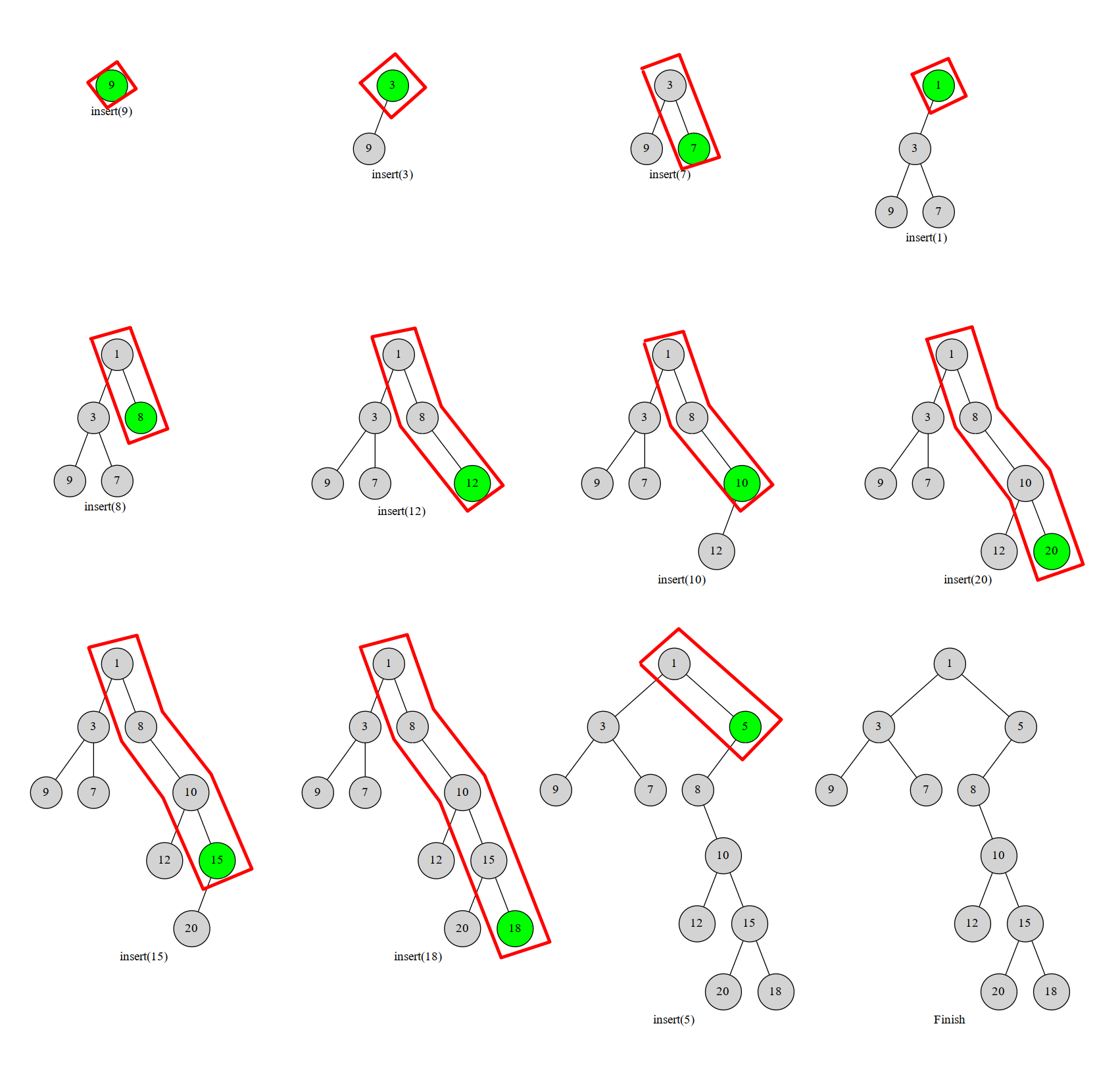
图中每个点进出栈最多一次,所以总的复杂度 (O(n))
实现代码:
// a是给定的数组,stc是栈,sc是栈顶,ls和rs分别表示左儿子和右儿子
for(int i = 1; i <= n; ++i) {
a[i] = read();
int k = sc; // 用栈维护右链,构建方法有点像虚树
while(k && a[stc[k]] > a[i]) k--; // 找到一个小于当前点的权值的点
if(k) rs[stc[k]] = i; // 让 i 成为这个点的右儿子
if(k < sc) ls[i] = stc[k + 1]; // 让这个点上挂着的点成为 i 的左儿子
stc[++k] = i; // 入栈
sc = k; // 更新栈顶
}
例题
P5854 【模板】笛卡尔树
直接建树,然后按要求求出答案就行
只放一个主函数,前面啥也没有
signed main()
{
n = read();
for(int i = 1; i <= n; ++i) {
a[i] = read();
int k = sc; // 用栈维护右链,构建方法有点像虚树
while(k && a[stc[k]] > a[i]) k--; // 找到一个小于当前点的权值的点
if(k) rs[stc[k]] = i; // 让 i 成为这个点的右儿子
if(k < sc) ls[i] = stc[k + 1]; // 让这个点上挂着的点成为 i 的左儿子
stc[++k] = i; // 入栈
sc = k; // 更新栈顶
}
for(int i = 1; i <= n; ++i) ans1 ^= (i * ls[i] + i), ans2 ^= (i * rs[i] + i);
printf("%lld %lld", ans1, ans2);
return 0;
}
P1377 [TJOI2011]树的序
题意是给出一个二叉搜索树的构建顺序,要求输出它的先序遍历。
朴素的建树方法最坏情况下会被卡成 (O(n^2))
这里考虑一种笛卡尔树的做法。
把给定序列的值看做下标 (k),下标看做权值 (w) 然后就可以 (O(n)) 建树了
为什么?
值要满足二叉查找树的限制,插入顺序上儿子比父亲晚插入,满足堆得性质。
因为给定的序列一定是 (1 sim n) 的一个序列,又因为它满足二叉搜索树,那么和我们笛卡尔树中的满足二叉搜索树的性质相同。一个元素越在序列后边,它在二叉搜索树中的位置越深,换句话说,对于一个数 (x) ,在它到根的路径上的点一定在序列的前面。所以可以把第几个插入看做权值 (w) 去构建笛卡尔树。
至于先序遍历,按“根左右”的顺序输出即可。
代码还是只给出重要部分:
void Print(int u) {
printf("%d ", u);
if(ls[u]) Print(ls[u]);
if(rs[u]) Print(rs[u]);
}
int main()
{
n = read();
for(int i = 1; i <= n; ++i) a[read()] = i;
for(int i = 1; i <= n; ++i) {
int k = sc;
while(k && a[stc[k]] > a[i]) --k;
if(k) rs[stc[k]] = i;
if(k < sc) ls[i] = stc[k + 1];
stc[++k] = i;
sc = k;
}
Print(stc[1]);
return 0;
}
P3246 [HNOI2016]序列
发现有很多用莫队和 RMQ 做的,不过这里我们只讲笛卡尔树做法
设 (f_{l, r}) 表示 (sum_{i = l}^{r}min_{lle jle i} {a_j}) 的答案
设 (pre_i) 表示 ((pre_i,i]) 这段区间内的最小值都是 (a_i),那么显然
发现这玩意与 (l) 无关,删掉第一维即可。
显然 (f_r = a_r imes (r - pre_r) + a_{pre_r} imes (pre_r - pre_{pre_r}) ...)
即 (f_r = sum_{i = 1}^r min_{ile j le r} {a_j})
设我们求区间 ([l,r]),区间最小值为 (a_p)
考虑左在 ((p,r]),右端点在 (r) 时的情况,
因为最终一定会有一个点 (x = pre_i),
所以 (f_r = a_r imes (r - pre_r) + a_{pre_r} imes (pre_r - pre_{pre_r}) + ... + f_p)
答案就是 (f_r - f_p)
对于所有右端点在 ((p,r]) 中的情况类似。
所以可以设 (g_r = sum_{i=1}^{r}f_i)
那么左右端点都在 ((p,r]) 中时的答案为 (g_r - g_p - f_p imes (r-p+1))
左右端点在 ([l,p)) 时用相同的方法处理即可。
对于点 (p) 可以利用笛卡尔树快速找到。
剩下的看代码
/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define int long long
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
int n, m, rt;
int a[MAXN];
int ls[MAXN], rs[MAXN];
int stc[MAXN], sc = 0;
int pre[MAXN], suf[MAXN];
int fl[MAXN], fr[MAXN], gl[MAXN], gr[MAXN];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
int Query(int l, int r) { // 找到区间最小点
int x = rt;
while(true) {
if(l <= x && x <= r) return x; // 先遍历到的在区间内的一定是最小点
x = (x > r ? ls[x] : rs[x]); // 要么在区间右边,要么在区间左边
}
}
int calc(int l, int r, int p) { // 计算答案
// return gr[r] - gr[l-1] - fr[p] * (r - l + 1);
return (p - l + 1) * (r - p + 1) * a[p] + gr[r] - gr[p] - fr[p] * (r - p) + gl[l] - gl[p] - fl[p] * (p - l);
}
signed main()
{
n = read(), m = read();
for(int i = 1; i <= n; ++i) {
a[i] = read();
int k = sc;
while(k && a[stc[k]] > a[i]) k--; // 建立笛卡尔树
if(k) rs[stc[k]] = i;
if(k < sc) ls[i] = stc[k + 1];
stc[++k] = i;
sc = k;
}
rt = stc[1];
sc = 0;
for(int i = 1; i <= n; ++i) {
while(sc && a[stc[sc]] > a[i]) sc--; // 维护两次单调栈,让 [pre[i], i] 这个区间的最小值都是 a[i]
pre[i] = stc[sc], stc[++sc] = i;
}
for(int i = 1; i <= n; ++i) {
fr[i] = fr[pre[i]] + a[i] * (i - pre[i]); // 利用推出来的式子进行预处理
gr[i] = gr[i - 1] + fr[i];
}
// for(int i = 1; i <= n; ++i) cout<<pre[i]<<" ";
// cout<<"
";
sc = 0;
for(int i = n; i >= 1; --i) {
while(sc && a[stc[sc]] > a[i]) sc--;
suf[i] = stc[sc], stc[++sc] = i;
}
for(int i = n; i >= 1; --i) {
fl[i] = fl[suf[i]] + a[i] * (suf[i] - i);
gl[i] = gl[i + 1] + fl[i];
}
// for(int i = 1; i <= n; ++i) cout<<suf[i]<<" ";
// cout<<"
";
for(int i = 1, l, r, p; i <= m; ++i) {
l = read(), r = read();
p = Query(l, r);
printf("%lld
", calc(l, r, p));
}
return 0;
}