@
http://libo-sober.top/mydata/PythonPrimAndKruskal.html
最小生成树(Prim算法、Kruskal算法)
生成树的定义
生成树是一个连通图G的一个极小连通子图。包含G的所有n个顶点,但只有n-1条边,并且是连通的。 生成树可由遍历过程中所经过的边组成(有多个)。
扩展:无向图。极小连通子图与极大连通子图是在无向图中进行讨论的。
连通图:在无向图中,若从定点V1到V2有路径,则称顶点V1和V2是连通的。如果图中任意一对顶点都是连通的,则称此图是连通图。(连通的无向图)
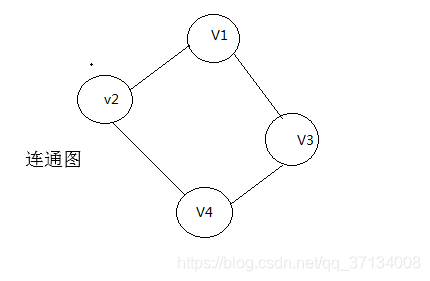
极小连通子图:
1.一个连通图的生成树是该连通图顶点集确定的极小连通子图。(同一个连通图可以有不同的生成树,所以生成树不是唯一的)
(极小连通子图只存在于连通图中)
2.用边把极小连通子图中所有节点给连起来,若有n个节点,则有n-1条边。如下图生成树有6个节点,有5条边。
3.之所以称为极小是因为此时如果删除一条边,就无法构成生成树,也就是说给极小连通子图的每个边都是不可少的。
4.如果在生成树上添加一条边,一定会构成一个环。
也就是说只要能连通图的所有顶点而又不产生回路的任何子图都是它的生成树。

最小生成树的定义
一个带权连通无向图的生成树中,边的权值之和最小的那棵树叫做此图的最小生成树。

图一的最小生成树就是图二(最小生成树在某些情况下并不唯一)。
最小生成树的生成算法:
求解最小生成树的算法主要有两个:
1.Prim(普里姆)算法;
2.Kruskal(克鲁斯卡尔)算法。
Prim算法
- 输入:一个加权连通图,其中顶点集合为V,边集合为E;
- 初始化:定义存放当前已走点的集合Vnew = {x},其中x为集合V中的任意节点(作为起始点),定义存放当前已走边的集合Enew = { },为空;
- 重复下列操作,直到 Vnew = V:
① 在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
② 将v加入集合Vnew中,将<u, v>边加入集合Enew中; - 输出:使用集合Vnew和Enew来描述所得到的最小生成树。
比如首先是一张图,然后是一些定义的空的变量集合:其中,当前可选点集U是指与当前已选点集中的点存在可达关系且未被标记为已选的所有点所构成的集合。

接下来我们随机选择一个点作为起点,比如选择V1作为初始点,则需要将V1加入Vnew集合,情况如下:

容易看出,在已选点集和可选点集连接形成的可选边中(<V1 ,V2>,<V1 ,V3>,<V1 ,V4>),边<V1 ,V3>的权值最小,因此需要将边<V1 ,V3>加入Enew集合,同时也需要将点V3加入Vnew集合,此时两个集合的情况如下:

接下来在已选点集和可选点集连接形成的可选边中(<V1 ,V2>,<V1 ,V4>,<V3 ,V2>,<V3 ,V4>,<V3 ,V5>,<V3 ,V6>),选择权值最小的边<V3 ,V6>,将其加入Enew集合,同时将点V6加入Vnew集合,此时两个集合的情况如下:

接着在已选点集和可选点集连接形成的可选边中(<V1 ,V2>,<V1 ,V4>,<V3 ,V2>,<V3 ,V4>,<V3 ,V5>,<V6 ,V4>,<V6 ,V5>),边<V6 ,V4>的权值最小,因此需要将边<V6 ,V4>加入Enew集合,同时也需要将点V4加入Vnew集合,此时两个集合的情况如下:

接着继续在已选点集和可选点集连接形成的可选边中(<V1 ,V2>,<V3 ,V2>,<V3 ,V5>,<V6 ,V5>),选择权值最小的边<V3 ,V2>,并将其加入Enew集合,同时将点V2加入Vnew集合,此时两个集合的情况如下:

接着继续在已选点集和可选点集连接形成的可选边中(<V2 ,V5>,<V3 ,V5>,<V6 ,V5>),选择权值最小的边<V2 ,V5>,并将其加入Enew集合,同时将点V2加入Vnew集合,此时两个集合的情况如下:

至此,集合Vnew = V,即所有的点都已经被选中,故结束循环。
此时,集合Vnew和Enew即可用于描述所得到的最小生成树(如上图中的红色部分)。
python栈和队列、二叉树
图的两种表示形式
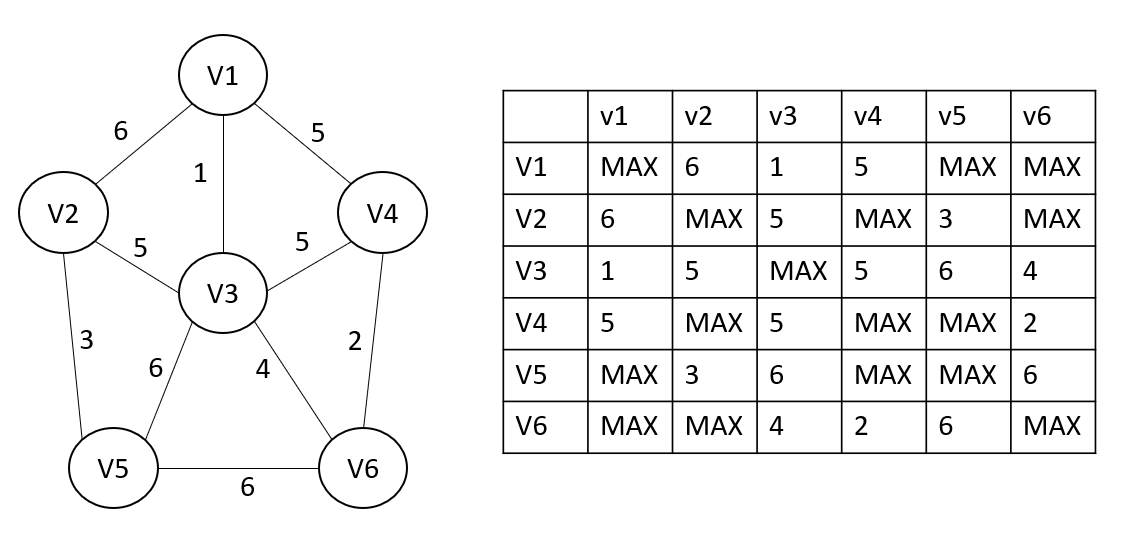
邻接矩阵
矩阵的每行和每列都代表图中的顶点,如果两个顶点之间有边相连,设定行列值。
无权边则将矩阵分量标注位1或0
带权的边则将权重保存为矩阵分量值。
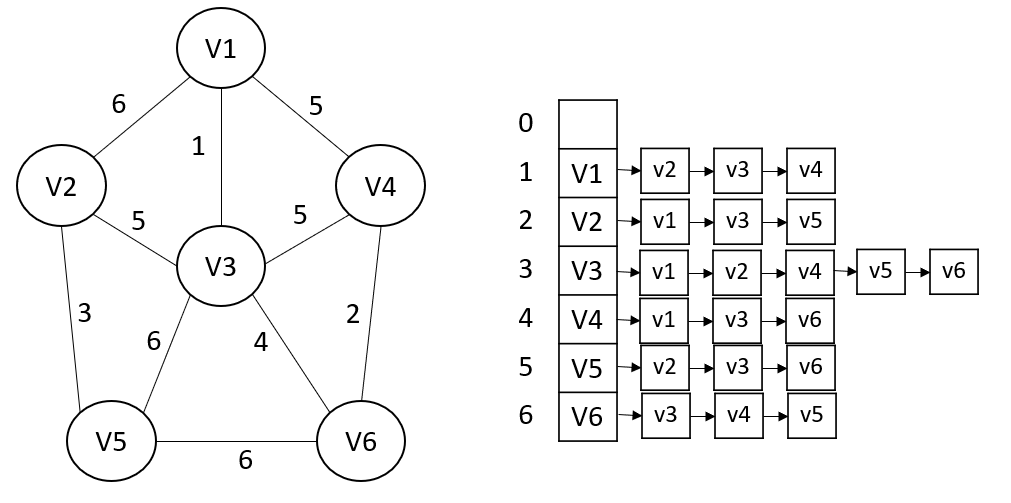
邻接表
邻接表(adjacent list)可以成为稀疏图的更高效实现方案。
它维护一个包含所有顶点的主列表,主列表中的每个顶点,再关联一个与自身右边连接的所有顶点的列表。
下面给出用编程语言实现的具体描述(Python):
"""
Prim类接受两个参数n,m,分别表示录入的点和边的个数(点的编号从1开始递增)
接下来是m行,每行3个数x,y,length,表示点x和点y之间存在一条长度为length的边
程序最终会打印出该无向图中的最小生成树的各个边和最小权值
"""
class Node:
"""
Node类存放节点信息,
node是与某个节点(实际上是用列表索引值代表的)相连接的点
length表示这两个点之间的权值
"""
def __init__(self, node, length):
self.node = node
self.length = length
class Edge:
"""
Edge类表示边的信息
x,y表示这条边的两个顶点
length为<x,y>之间的距离
"""
def __init__(self, x, y, length):
self.x = x
self.y = y
self.length = length
class Prim:
"""Prim算法:求解无向连通图中的最小生成树 """
def __init__(self, n, m):
self.n = n # 输入的点个数
self.m = m # 输入的边个数
self.v = [[] for i in range(n+1)] # 存放所有节点之间的可达关系与距离
"""图的邻接表的表示法,v是一个二维列表,其索引值代表当前节点,索引值对应的一维列表中存放的
是与以当前索引值为顶点的相连的节点信息"""
self.e = [] # 存放与当前已选节点相连的边
"""e是一个一维列表,存放的是与当前顶点相连的所有的边的信息"""
self.s = [] # 存放最小生成树里的所有边
self.vis = [False for i in range(n+1)] # 标记每个点是否被访问过,False未访问
def graphy(self):
"""构建图,这里用的是邻接表"""
for i in range(self.m):
x, y, length = list(map(int, input().split()))
self.v[x].append(Node(y, length)) # 与x相连的y节点记录在二维列表v的x索引值对应的一维列表中
self.v[y].append(Node(x, length)) # 与y相连的x节点记录在二维列表v的y索引值对应的一维列表中
# print(self.v)
def insert(self, point):
"""往Vnew中插入一个新的点"""
for i in range(len(self.v[point])):
"""把与point节点相连的且未被访问的节点的边加入列表e中"""
if not self.vis[self.v[point][i].node]:
self.e.append(Edge(point, self.v[point][i].node, self.v[point][i].length))
self.vis[point] = True
self.e = sorted(self.e, key=lambda e: e.length) # 把e中的所有边按边的长度从小到大排序
# for i in self.e:
# print(i.length)
def run(self, start):
"""执行函数:求解录入的无向连通图的最小生成树"""
self.insert(start) # start为选择的开始顶点
while self.n - len(self.s) > 1: # 最小生成树的边数=图中节点数-1,因此可以利用这个性质来作为循环条件
for i in range(len(self.e)): # 按序遍历所有边
if not self.vis[self.e[i].y]: # 如果待检测的第二个位置上的点未访问过,则说明这条边满足一端在Vnew中,另一端不在
self.s.append(self.e[i]) # 则需要将该边放进结果集合中,因为第一个遇到的肯定是权值最小的,在插入函数中已经排好序了
self.insert(self.e[i].y) # 同时将该边的另一个节点插入Vnew中
break # 找到一条符号条件的便后就退出for循环
def print(self):
"""输出信息"""
print(f'当前录入总边数为:{len(self.e)}
其中构成最小生成树的边为:')
edge_sum = 0
for i in range(len(self.s)):
print(f'边<{self.s[i].x},{self.s[i].y}> = {self.s[i].length}')
edge_sum += self.s[i].length
print(f'最小生成树的权值为:{edge_sum}')
def main():
n, m = list(map(int, input().split()))
prim = Prim(n, m)
prim.graphy()
prim.run(1)
prim.print()
if __name__ == '__main__':
main()
在程序运行时,输入以下内容:
6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6
运行结果:
6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6
当前录入总边数为:10
其中构成最小生成树的边为:
边<1,3> = 1
边<3,6> = 4
边<6,4> = 2
边<3,2> = 5
边<2,5> = 3
最小生成树的权值为:15
Process finished with exit code 0
Kruskal算法
- 设无向连通图Graph有v个顶点,e条边;
- 新建图Graphnew,Graphnew拥有与原图中相同的v个顶点,但没有边;
- 将原图Graph中所有边按权值从小到大排序;
- 进入一层循环,该循环从权值最小的边开始遍历每条边,直至图Graphnew中所有的节点都在同一个连通分量中。循环体内的内容如下:
if(这条边连接的两个节点于图Graphnew中不在同一个连通分量中) 则添加这条边到图Graphnew中;
下面我们还是用前面的图一来进行举例说明,首先是将原图中的所有边按权值从小到大进行排序,如下:

然后是建立一个没有任何边的图Graphnew,如下(注:这里的没有边是指没有被描红的边):

接下来我们开始遍历上面给出的那个表,首先遍历到的第一条边是<V1,V3>,长度为1。由于在当前图中,节点V1和V3并不连通,因此可以将这条边添加到上图中(即标红,下同),如下:

接下来是第二条边<V4,V6>,长度为2。在当前图中,节点V4和V6并不连通,因此可以将这条边添加到上图中,如下:

然后是第三条边<V2,V5>,长度为3。在当前图中,节点V2和V5并不连通,因此可以将这条边添加到上图中,如下:

继续往下是第四条边<V3,V6>,长度为4。在当前图中,节点V3和V6并不连通,因此可以将这条边添加到上图中,如下:

然后是第五条边<V1,V4>,长度为5。注意到在当前图中,节点V1和V4已经在同一个连通分支中,因此不能将这条边添加进来,于是跳过这条边,继续往下。
接着是第六条边<V2,V3>,长度也为5。在当前图中,节点V2和V3并不连通,因此可以将这条边添加到上图中,如下:

至此,我们发现图Graphnew中的所有节点都在同一个连通分支中,因此循环结束。
此时,边集E即可用于描述所得到的最小生成树(如上图中的红色部分)。
下面给出用编程语言实现的具体描述(python):
"""
Kruskal类接受两个参数n,m,分别表示录入的点和边的个数(点的编号从1开始递增)
接下来是m行,每行3个数x,y,length,表示点x和点y之间存在一条长度为length的边
程序最终会打印出该无向图中的最小生成树的各个边和最小权值
"""
class Edge:
"""
Edge类表示边的信息
x,y表示这条边的两个顶点
length为<x,y>之间的距离
"""
def __init__(self, x, y, length):
self.x = x
self.y = y
self.length = length
class UnionFindSet:
"""并查集类,用于连通两个节点以及判断图中的所有节点是否连通 """
def __init__(self, start, n):
self.start = start # start和n分别用于指示并查集里节点的起点和终点
self.n = n
self.pre = [0 for i in range(self.n - self.start + 2)] # pre数组用于存放某个节点的上级
self.rank = [0 for i in range(self.n - self.start + 2)] # rank数组用于降低关系树的高度
def init(self):
"""初始化并查集"""
for i in range(self.start, self.n+1):
self.pre[i] = i
self.rank[i] = 1
def find_pre(self, x):
"""寻找节点x的上一级节点"""
if self.pre[x] == x:
return x
else:
self.pre[x] = self.find_pre(self.pre[x])
return self.pre[x]
def is_same(self, x, y):
"""判断x节点和y节点是否连通"""
return self.find_pre(x) == self.find_pre(y)
def unite(self, x, y):
"""判断两个节点是否连通,如果未连通则将其连通并返回真,否则返回假"""
x = self.find_pre(x)
y = self.find_pre(y)
if x == y:
return False
if self.rank[x] > self.rank[y]:
"""类似于平衡二叉树的概念"""
self.pre[y] = x
else:
if self.rank[x] == self.rank[y]:
self.rank[y] += 1
self.pre[x] = y
return True
def is_one(self):
"""判断整个无向图中的所有节点是否连通 """
temp = self.find_pre(self.start)
for i in range(self.start+1, self.n+1):
if self.find_pre(i) != temp:
return False
return True
class Kruskal:
"""Kruskal算法:求解无向连通图中的最小生成树 """
def __init__(self, n, m):
self.n = n # n,m分别表示输入的点和边的个数
self.m = m
self.e = [] # 存放录入的无向连通图的所有边
self.s = [] # 存放最小生成树里的所有边
self.u = UnionFindSet(1, self.n) # 并查集:抽象实现Graphnew,并完成节点间的连接工作以及判断整个图是否连通
def graphy(self):
"""这里只是存储所有边的信息并按边的长度排序"""
for i in range(self.m):
x, y, length = list(map(int, input().split()))
self.e.append(Edge(x, y, length))
self.e.sort(key=lambda e: e.length)
# for i in self.e:
# print(i.length)
self.u.init()
def run(self):
"""执行函数:求解录入的无向连通图的最小生成树 """
for i in range(self.m):
if self.u.unite(self.e[i].x, self.e[i].y):
self.s.append(self.e[i])
if self.u.is_one():
"""一旦Graphnew的连通分支数为1,则说明求出了最小生成树 """
break
def print(self):
print(f'构成最小生成树的边为:')
edge_sum = 0
for i in range(len(self.s)):
print(f'边 <{self.s[i].x},{self.s[i].y}> = {self.s[i].length}')
edge_sum += self.s[i].length
print(f'最小生成树的权值为:{edge_sum}')
def main():
n, m = list(map(int, input().split()))
kruskal = Kruskal(n, m)
kruskal.graphy()
kruskal.run()
kruskal.print()
if __name__ == '__main__':
main()
运行结果:
6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6
构成最小生成树的边为:
边 <1,3> = 1
边 <4,6> = 2
边 <2,5> = 3
边 <3,6> = 4
边 <2,3> = 5
最小生成树的权值为:15