T1铺设道路
传送门
题目描述
春春是一名道路工程师,负责铺设一条长度为 $ n $ 的道路。
铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 $ n $ 块首尾相连的区域,一开始,第 ii 块区域下陷的深度为 $ d[i] $ 。
春春每天可以选择一段连续区间 $ [L,R] $ ,填充这段区间中的每块区域,让其下陷深度减少 $ 1 $ 。在选择区间时,需要保证,区间内的每块区域在填充前下陷深度均不为 $ 0 $ 。
春春希望你能帮他设计一种方案,可以在最短的时间内将整段道路的下陷深度都变为 $ 0 $ 。
输入输出格式
输入格式:
输入文件包含两行,第一行包含一个整数 $ n $ ,表示道路的长度。 第二行包含 $ n $ 个整数,相邻两数间用一个空格隔开,第 $ i $ 个整数为 $ d[i]$ 。
输出格式:
输出文件仅包含一个整数,即最少需要多少天才能完成任务。
输入输出样例
输入样例
6
4 3 2 5 3 5
输出样例
9
说明
【样例解释】
一种可行的最佳方案是,依次选择: $ [1,6] $ , $ [1,6] $ , $ [1,2] $ , $[1,1] $ , $ [4,6] $ , $ [4,4] $ , $ [4,4] $ , $ [6,6] $ , $ [6,6] $ 。
【数据规模与约定】
对于 $ %30 $ 的数据, $ 1 ≤ n ≤ 10 $ ;
对于 $ %70 $ 的数据, $ 1 ≤ n ≤ 1000 $ ;
对于 $ %100 $ 的数据,$ 1 ≤ n ≤ 100000 $ , $ 0 ≤ d[i]≤ 10000 $
分析:
整体想法是用一个 $ while $ 循环来控制指针,找出每一段不上升的子序列,将这些子序列中的第一个数加起来,因为这个数是这一段子序列中最大值,所以这个数就是这一整个序列铺设道路所用的最少时间,然后加起来就好了。
还有我觉得开始处理或者是不处理出一个最小值都没有关系。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
#include <queue>
#include <map>
#include <cmath>
#define re register
using namespace std ;
const int maxn = 100005 ;
inline int read() {
int f = 1 , x = 0 ;
char ch = getchar() ;
while(ch < '0' || ch > '9') {if(ch == '-') f = -1 ; ch = getchar() ;}
while(ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + ch - '0' ;ch = getchar() ;}
return x * f ;
}
int n , h[maxn] ;
int tmp , ans , minn = 1e9 ;
int main() {
n = read() ;
for(re int i = 1 ; i <= n ; ++i) {
h[i] = read() ;
minn = min(minn , h[i]) ;
}
ans += minn ;
for(re int i = 1 ; i <= n ; ++i) h[i] -= minn ;
int j = 1 ;
while(h[j] == 0) j++ ;
int wh = 0 , m = 1e9 ;
while(j <= n) {
m = h[j] ;
ans += (h[j] - h[wh]) ;
for(int i = j ; i <= n ; ++i) {
if(h[i] <= m) {
m = h[i] ;
wh = i ;
}
else break;
}
j = wh + 1;
}
printf("%d
" , ans) ;
return 0 ;
}
T2货币系统
传送门啦
题目描述
在网友的国度中共有 $ n $ 种不同面额的货币,第 $ i $ 种货币的面额为 $ a[i] $ ,你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为 $ n $ 、面额数组为 $ a[1..n] $ 的货币系统记作 $ (n,a) $ 。
在一个完善的货币系统中,每一个非负整数的金额 $ x $ 都应该可以被表示出,即对每一个非负整数 $ x $ ,都存在 $ n $ 个非负整数 $ t[i] $ 满足 $ a[i] imes t[i] $ 的和为 $ x $ 。然而, 在网友的国度中,货币系统可能是不完善的,即可能存在金额 $ x $ 不能被该货币系统表示出。例如在货币系统 $ n=3, a=[2,5,9] $ 中,金额 $ 1,3 $ 就无法被表示出来。
两个货币系统 $ (n,a) $ 和 $ (m,b) $ 是等价的,当且仅当对于任意非负整数 $ x $ ,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。他们希望找到一个货币系统 $ (m,b) $ ,满足 $ (m,b) $ 与原来的货币系统 $ (n,a) $ 等价,且 $ m $ 尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的 $ m $ 。
输入输出格式
输入格式:
输入文件的第一行包含一个整数 $ T $ ,表示数据的组数。
接下来按照如下格式分别给出 $ T $ 组数据。 每组数据的第一行包含一个正整数 $ n $ 。接下来一行包含 $ n $ 个由空格隔开的正整数 $ a[i] $
输出格式:
输出文件共有 $ T $ 行,对于每组数据,输出一行一个正整数,表示所有与 $ (n,a) $ 等价的货币系统 $ (m,b) $ 中,最小的 $ m $ 。
输入输出样例
输入样例:
2
4
3 19 10 6
5
11 29 13 19 17
输出样例:
2
5
说明
在第一组数据中,货币系统 $ (2, [3,10]) $ 和给出的货币系统 $ (n, a) $ 等价,并可以验证不存在 $ m < 2 $ 的等价的货币系统,因此答案为 $ 2 $ 。 在第二组数据中,可以验证不存在 $ m<n $ 的等价的货币系统,因此答案为 $ 5 $ 。
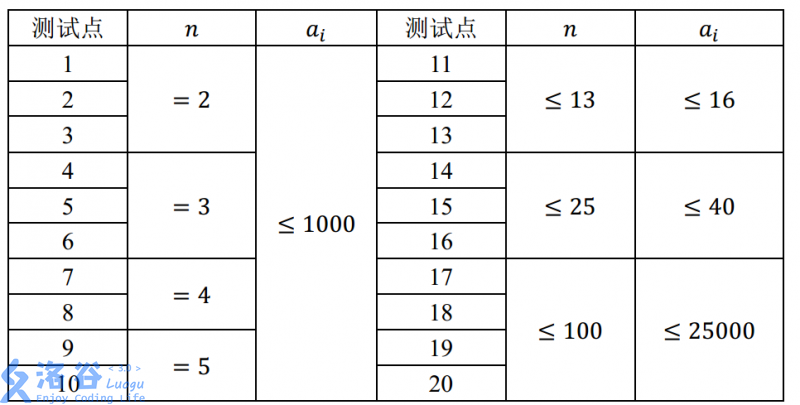
分析:
首先相同的数字肯定是没有意义的,我们对原数组进行去重,然后我们用一个数组 $ vis[i] $ 表示数字 $ i $ 是否能够表示,如果 $ vis[i]=true $ 可以表示,否则不可以表示。那么我们就对于 $ n $ 个数中的每一个数字进行判断,第一个 $ a[0] $ 肯定不能表示,那么我们结果 $ ans++ $ , 然后把 $ a[0] $ 能够表示的数字 $ i $ 全标记为 $ vis[i]=true $ ;那么在检查第 $ i $ 个数字,如果能够用已经标记的数字表示,那么说明这个数可以用 之前的数表示,答案不记录;否则答案记录,而且将已经能够表示的数字加上 $ a[i] $ ,也进行标记 $ vis[j+a[i]]=true $ ,直至循环完毕,输出 $ ans $ 即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
#include <queue>
#include <map>
#include <vector>
#include <cmath>
#define re register
using namespace std ;
const int maxn = 105 ;
const int Maxn = 25005 ;
inline int read() {
char ch = getchar() ;
int f = 1 , x = 0 ;
while(ch > '9' || ch < '0') {if(ch == '-') f = -1 ; ch = getchar() ;}
while(ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + ch - '0' ; ch = getchar() ;}
return x * f ;
}
int T , n , a[maxn];
int f[maxn] , ans;
bool vis[Maxn] ;
int main() {
T = read() ;
while(T--) {
n = read() ;
memset(a , 0 , sizeof(a)) ;
for(re int i = 1 ; i <= n ; ++i) {
a[i] = read() ;
}
sort(a + 1 , a + 1 + n) ;
n = unique(a + 1 , a + 1 + n) - a - 1;
memset(vis , false , sizeof(vis)) ;
vis[0] = true ;
ans = 0 ;
for(re int i = 1 ; i <= n ; ++i) {
if(!vis[a[i]]) {
ans ++ ;
for(re int j = 0 ; j < Maxn ; ++j)
if(j + a[i] < Maxn && vis[j])
vis[j + a[i]] = true ;
}
}
printf("%d
" , ans) ;
}
return 0 ;
}