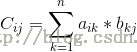矩阵快速幂

一、基础知识

1、矩阵的定义

!

2、行矩阵和列矩阵应该比较好理解，就是一个矩阵的每一行都可以称之为一个行矩阵，同理列矩阵也一样。

3、同型矩阵：设有矩阵A和矩阵B，矩阵A的行数和列数都与矩阵B的相同，则矩阵A、B是同型矩阵

像图中这样就是两个同型矩阵

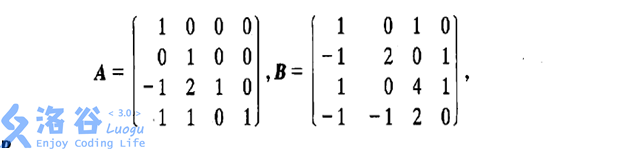
4、单位矩阵

在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1,这种矩阵被称为单位矩阵．

它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0。

二、矩阵的相关运算

1、矩阵加法

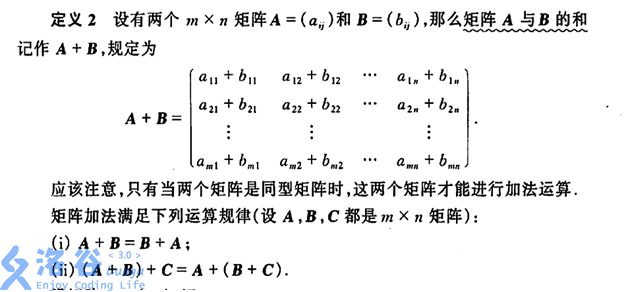
图上说的也很清楚了吧，矩阵加法满足加法交换律和加法结合律。

2、矩阵乘法

结合图片理解一下吧。

其中，c[i][j]表示：矩阵A的第 i 行与矩阵B的第 j 列的对应乘积的和。

也就是

2、矩阵快速幂引入

为了引出矩阵快速幂，我们先来学整数快速幂，加入我们要计算如果现在要算X^8：则 XXXXXXXX 按照寻常思路，一个一个往上面乘，则乘法运算进行7次。

(XX)(XX)(XX)(XX)
这种求法，先进行乘法得X^2,然后对X2再执行三次乘法，这样去计算，则乘法运算执行4次。已经比七次要少。所以为了快速算的整数幂，就会考虑这种结合的思想。

现在要考虑应该怎么分让计算比较快。接下来计算整数快速幂。例如：X^19次方。

19的二进制为：1 0 0 1 1 。

由(X^m)(Xn) = X^(m+n)

则X^19 = (X^16)(X2)*(X^1)

那么怎么来求解快速幂呢。请看下列代码：
求解X^N的值。

int quickpow(int x,int N){
	int res = x;
    int ans = 1;
    while(N){
    	if(N & 1）{
        	ans = ans * res;
        }
        res = res * res;
        N = N >> 1;
    }
    return ans;
}

那现在，我们来仔细看一下这个代码。

对于x^19来说，19的二进制是1 0 0 1 1

初始化

ans = 1;  res = x;

因为19的二进制最后一位是 1 ，所以19是奇数。

ans = res * ans = x ; 

res = res * res = x ^ 2;

然后右移一位，就变成了1 0 0 1

则最后一位是 1 ，所以是奇数。

ans = ans * res 
    = x * (x ^ 2) = x ^ 3;

res = res * res
    = x ^ 2 * x ^ 2
    = x ^ 4;

然后右移一位，变成了1 0 0

则最后一位是 0 ，所以是偶数。

res = res * res 
    = x ^ 4 * x ^ 4
    = x ^ 8;

然后右移一位，变成了1 0

则最后一位是偶数。

res = res * res 
    = x ^ 8 * x ^ 8
    = x ^ 16;

然后右移一位，只剩下 1 了。

还看吗？肯定是奇数

ans = ans * res 
    = (x ^ 3) *（x ^ 16） 
    = x ^ 19
    
res = res * res = x ^ 32

总结一下：

  从上述叙述中可以看出res = x ^ m
  始终是与二进制位置上的权值是相对应的。
  
  当二进制位是 0 时 ， 我们只让res ^ 2,来对应二进制下一位的权值
  当二进制位是 1 时 ， ans = ans * res , 再使res ^ 2

说了一大堆，我们进入正题，矩阵快速幂

假如现在有一个n * n的方阵A。给出一个数M，让算矩阵A的M次幂，A ^ M.则上面代码可以化为。

struct matrix{
	int m[maxn][maxn];
}ans , res;//这是计算矩阵乘法的参数

//我们假设参数矩阵是 A 、B和一个数n(表示n * n)

matrix mul(matrix A,matrix B){
	matrix tmp;
    //这是我们临时设置的一个矩阵，存A*B的结果
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
        tmp.m[i][j] = 0;
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
        for(int k=1;k<=n;k++)
          tmp.m[i][j] += A.m[i][k] * B.m[k][j];
    return tmp;
}

//快速幂算法，求矩阵res的N次幂

matrix quickpower(matrix res,int x){
	/*我们在上面介绍整数幂的时候将ans初始化为 1
      但对于矩阵乘法来说，ans应该初始化为单位矩阵
      现在补充一个单位矩阵的性质：
      单位矩阵乘任意矩阵都是原矩阵
    */
    for(int i=1;i<=n;i++)//单位矩阵定义方法
      for(int j=1;j<=n;j++){
        if(i == j)  ans.m[i][j] = 1;
        else  ans.m[i][j] = 0;
      }
    while(x){
      if(x & 1)
         ans = mul(ans , res);
      res = mul(res , res);
      x = x >> 1;
    }
}

贴上一个完整的代码吧：
P3390 矩阵快速幂模板

#include <cstdio>
#include <istream>
#include <cstring>
#include <algorithm>
#include <cmath>//pow函数，其实没啥用 
using namespace std;
const int mod = pow(10,9)+7;

long long n,k;
struct matrix{
	long long m[105][105];
}ans , res;

matrix mul(matrix x,matrix y){
    matrix tmp;
	for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
        tmp.m[i][j] = 0;
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
        for(int k=1;k<=n;k++)
          tmp.m[i][j] = tmp.m[i][j] % mod + (x.m[i][k] * y.m[k][j]) % mod;
    return tmp;
}

matrix quickpower(matrix res,long long k){
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++){
        if(i == j)  ans.m[i][j] = 1;
        else  ans.m[i][j] = 0;
      }
    while(k){
        if(k & 1)
          ans = mul(ans , res);
        res = mul(res , res);
        k = k >> 1;
    }
    return ans;
}

int main(){
    scanf("%lld%lld",&n,&k);
    for(int i=1;i<=n;i++){ 
        for(int j=1;j<=n;j++)
            scanf("%lld",&res.m[i][j]);
    }       
    ans = quickpower(res , k);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++)
            printf("%lld ",ans.m[i][j] % mod);
        printf("
");
    }
    return 0;   
}

当然，矩阵快速幂还有另一种写法，用重载运算符重载 * 嘛

代码我就不解释了

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

#define ll long long

using namespace std;
const int N = 110;
const int MOD = 1e9 + 7;

ll n,k;
struct martix {
    ll a[N][N];
    martix operator*(const martix &b) const {
        martix x;
        for(int i = 1 ; i <= n ; i++) {
            for(int j = 1 ; j <= n ; j++) {
                x.a[i][j] = 0;
                for(int k = 1 ; k <= n ; k++) {
                    x.a[i][j] += a[i][k] * b.a[k][j];
                    x.a[i][j] %= MOD;
                }
            }
        }   
        return x;
    }
}mart;
martix quick_pow(martix x,ll y) {
    martix ans = x,s = x;
    for( ; y ; y >>= 1) {
        if(y & 1) ans=ans * s;
        s = s * s;
    }
    return ans;
}

int main() {
    scanf("%lld%lld",&n,&k);
    for(int i = 1 ; i <= n ; i++) {
        for(int j = 1 ; j <= n ; j ++) {
            scanf("%lld",&mart.a[i][j]);
        }
    }
    mart = quick_pow(mart,k - 1);
    for(int i = 1 ; i <= n ; i++) {
        for(int j = 1 ; j <= n ; j ++) 
            printf("%lld ",mart.a[i][j]);
        printf("
");
    }
    return 0;
}

上面只是简单的计算矩阵的幂，可能会感觉很抽象，因为上述矩阵并没有具体的含义，
现在就举例说明矩阵快速幂在实际运用中的意义：

以最常见的斐波那契数列为例：众所周知：斐波那契数列递推公式为：
F[n] = F[n-1] + F[n-2].

由f[0]=0,f[1]=1,可以递推后面的所有数。

在以前，我们会常常用for循环，这是最直接的算法。

但是，n 等于十亿你该怎么用for循环呢。。

好吧，在介绍矩阵快速幂，肯定是用矩阵快速幂来写。。