题意是问在给定的三角形数阵中从一个数到另一个数所要跨过的边数。
最初的时候很迷,除了发现每层的数字个数与层数间的关系和每层数最后一个数与层数的关系外什么也没看出来,打算先求出数字所在的层数,然后计算到该层最后一个数要跨过的边数,由于各层最后一个数之间所跨过的边数与层数差有关(称层数距离),
因此可以求得一条路线:如图
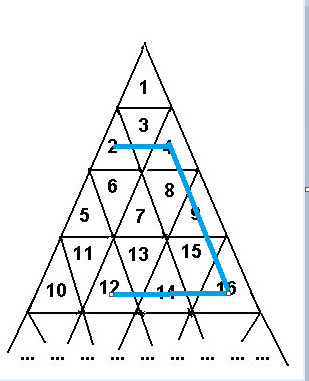
但两数间的最短路线依然求不到,感觉也不能用到每层最后一个数所跨边数作差,而层数距离也不一定会体现在最短路径中,比如 7 和 13 这一组,就只跨一条边即可。
借鉴了别人的博客,才知道了原图是要拆开看的:
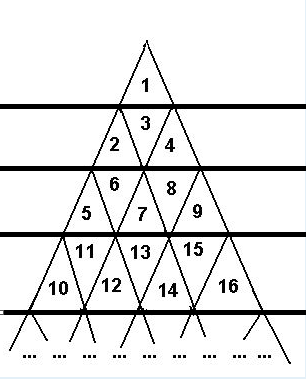
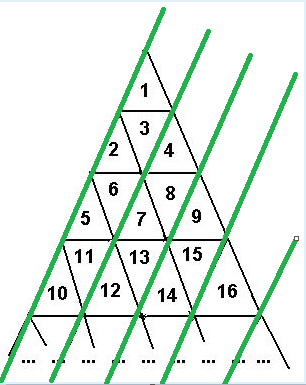
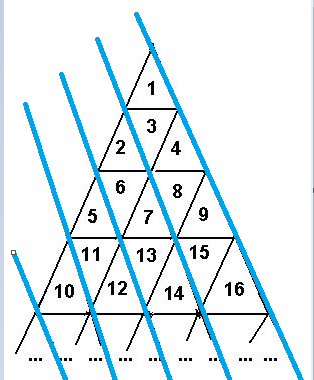
用这种方式分别分层之后,再去计算在每张图中跨过了多少层,然后对每张图中的层数差的绝对值求和即为结果。
另外,这道题很坑的一点是没说清楚输入有多少组,一直以为是只有一组,然后一直 wa...... 还是每次都让其输入到文件末靠谱一点。
代码如下:

1 #include<bits/stdc++.h> 2 using namespace std; 3 int getp(int n) 4 { 5 // int i = 1; 6 // while(i * i < n) ++i; 7 // return i; 8 return (int)ceil(sqrt(n)); 9 } 10 int main() 11 { 12 int m,n,pm,pn,pm1,pm2,pn1,pn2,ans; 13 while(~scanf("%d%d",&m,&n)) 14 { 15 pm = getp(m); 16 pn = getp(n); 17 pm1 = ((m-(pm-1)*(pm-1)-1)>>1)+1; 18 pn1 = ((n-(pn-1)*(pn-1)-1)>>1)+1; 19 pm2 = ((pm*pm-m)>>1)+1; 20 pn2 = ((pn*pn-n)>>1)+1; 21 ans = abs(pm-pn) + abs(pm1-pn1) + abs(pm2-pn2); 22 printf("%d ",ans); 23 } 24 return 0; 25 }
