树状数组套权值线段树

1.引言

树状数组套线段树可以以(O(nlogn))的优秀复杂度维护带修改操作的区间K小值和带修改操作的区间大于/小于K的值的个数的问题.

一些人也把这种树套树的结构叫做树状数组套主席树.事实上,在这种树套树中,内层的每一颗线段树是独立的,并不是类似于可持久化线段树(广泛被接受的"主席树")那样的"互相依存"的线段树.但是由于"主席树"在(OI)界定义并不明确,有些语境下也可以把动态开点的线段树称为主席树.本文对于内层的树统一采用"线段树/动态开点线段树"的称呼.

2.前置知识(都学到树套树了怎么可能不会)

• 前缀和/树状数组LG3374【模板】树状数组 1

• 普通线段树/权值线段树/动态开点线段树LG3372【模板】线段树 1

• 主席树求静态区间K小值LG3834【模板】可持久化线段树 1（主席树）

3.原理

3.1从位置到值域

在用数据结构维护一个数列时,我们通常会看到两种维护方式:

3.1.1维护方式(1)

以位置为下标,值为内容,比如最基础的线段树,当我们执行查询操作,比如查询[3,8],得到的是"原数列中第3个数到第8个数"的某些信息(和/最值)等.

3.1.2维护方式(2)

以值域为下标,值出现的次数为内容,比如用树状数组求逆序对,如果查询[3,8],得到的结果是值在[3,8]内的数的出现次数.

我们把采用维护方式(2)的线段树叫做权值线段树,根据线段树自带的"二分"属性(每一个节点二分为左子节点和右子节点),我们可以用权值线段树来求解动态全局(K)小值的问题.

3.2从前缀和到树状数组

3.2.1问题(1)

首先来思考一个很简单的问题:给你一个数列,不修改,多次询问区间和,怎么做?

太简单了!前缀和搞一搞就可以了.

具体来说,开一个长度为(n)的数组(记为(a)),(a_i)维护第(1)个数字到第(i)个数字的和,那么要查询([L,R])这个区间的和,只需要用(a_R)减去(a_{L-1})就可以了.

3.2.2问题(2)

再来一个问题:给你一个数列,不修改,多次询问区间第K小值,怎么做?

没错!就是静态区间(K)小,主席树的模板题!

太简单了!主席树搞一搞就可以了!

这里就需要理解主席树求静态区间K小值的原理.其实就是前缀和的思想:开(n)颗权值线段树,第(i)颗维护第(1)个数字到第(i)个数字的值域的信息,那么要查询([L,R])这个区间的权值的(K)小值,只需要用第(R)颗权值线段树减去第(L-1)颗权值线段树,再按上文(3.1.2)的思路求([L,R])区间(K)小值.

那开(n)颗权值线段树会爆空间怎么办?可持久化一下就好了.

看不懂?回去复习静态区间(K)小

3.2.3问题(3)

给你一个数列,边修改边询问,多次询问区间和,怎么做?

太简单了!树状数组维护前缀和搞一搞就可以了.

具体来说,开一个长度为(n)的数组(记为(c)),也就是树状数组的那个数组.如果要查询([1,i])前缀和,只需要把不多于(log_2i)个(c)值加起来就可以了.修改时,也只需要修改不多于(log_2i)个(c)值.复杂度(O(log_2n)).

看不懂?回去复习树状数组

3.2.4问题(4)

给你一个数列,边修改边询问,多次询问区间第K小值,怎么做?

没错!就是动态区间(K)小值的模板题!

结合(3.2.2)和(3.2.3)的思想,我们可以开(n)颗权值线段树,用树状数组维护(权值线段树相当于树状数组的节点).

如果要查询区间([1,i])的值域的信息,只需要把不多于(log_2i)颗线段树加起来就可以了.那么,如果要查询区间([L,R]) 的值域信息,我们先把(log_2i)颗线段树加起来求([1,R])的信息,再把把(log_2i)级颗线段树加起来求([1,L-1])的信息,然后用([1,R])的信息减掉([1,L-1])的信息,像(3.2.2)那么求就可以了.(不知道怎么加或者怎么求?回去读(3.2.2)).

修改时,也只需要修改不多于(log_2i)颗线段树.修改(1)颗线段树花费时间(O(log_2n)),那么(1)次修改总时间就是(O(log_2^2n)).

修改的复杂度好像对了,但是查询的相加那一步,累加(1)颗怎么着也得(O(n)),还要累加(log_2i)颗,单次复杂度达到了(O(nlogn)).怎么办?下一节我们再说.

到这里,我们也解决了刚学树状数组套线段树的人(比如当时的我)很纠结的问题——内层的线段树存的是什么?

我问你:树状数组的那个数组存的是什么?

是不是一时语塞,只可意会不可言传?

没错,这里的线段树存的东西就类似于那个数组存的东西.

4.代码实现

4.1离散化

容易发现,我们的内层权值线段树是基于值域的,如果题目中值的范围过大,需要进行离散化.带修改操作时,需要把修改的值也输入进来,同初始权值一起离散化.

4.2修改操作

和普通动态开点线段树的修改一样.如果进入空节点则新建节点.选择进入修改左右子树之一.

4.2.1示例代码

   //在内层线段树中
    void change(int &x,int L,int R,int Pos,int k)
    {
        if(x==0)x=++Tot;
        v[x]+=k;
        if(L==R)return;
        int Mid=(L+R)>>1;
        if(Pos<=Mid)change(LC[x],L,Mid,Pos,k);
        else change(RC[x],Mid+1,R,Pos,k);
    }
   //在外层树状数组中
	void change(int p,int val,int v)
    {
        for(int i=p;i<=n;i+=i&-i)
            SegmentTree.change(SegmentTree.Root[i],1,n,val,v);
    }

4.2.2注意

值得注意的是,如果上面的分析看懂了的话,会发现外层的树状数组是以位置为下标的.这也是我们在外层树状数组修改时既需要传位置的下标(代码里的(p)),也要传值(即内层线段树的下标,代码里的(val))的原因.

4.3权值线段树相加的方法

为了优化在(3.2.4)中提到的"把线段树加起来这一步复杂度过高的问题,我们有两种思路:

4.3.1单独计算,累计答案

有时候,题目所询问的并不是(相对的)排名,而是(绝对的)值,即动态询问区间大/小于(K)的值的个数,我们发现在求解这个问题时,每颗线段树是各自独立的.换句话说,我们不需要真的把这些线段树加起来,只需要在每个线段树中算出这(1)颗线段树的答案,再把这(logn)颗线段树的答案加起来就可以了.这样的话,每颗线段树查询(1)次是(O(logn))的,一共有(O(logn))颗线段树,单次查询的总复杂度就是(O(log_2^2n)).

没看懂?我们借助图像来理解:

原来的思路:

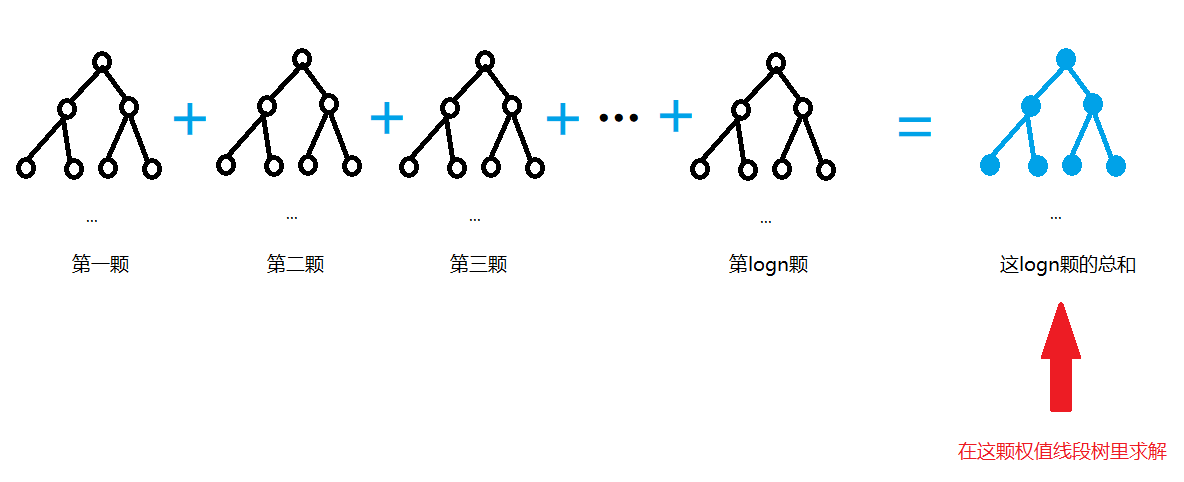
单独计算,累计答案的思路:

示例代码:

    //内层线段树
	int query(int x,int L,int R,int X,int Y)
    {
        if(x==0||L>Y||R<X)return 0;
        if(L>=X&&R<=Y)return val[x];
        int Mid=(L+R)>>1;
        return query(LC[x],L,Mid,X,Y)+query(RC[x],Mid+1,R,X,Y);
    }
	//外层树状数组
    int sum(int p,int Lx,int Rx)
    {
        int x=0;
        for(int i=p;i;i-=i&-i)x+=SegmentTree.query(SegmentTree.Root[i],1,n,Lx,Rx);
        return x;
    }
    int query(int L,int R,int Lx,int Rx)
    {
        if(Lx>Rx||L>R)return 0;
        return sum(R,Lx,Rx)-sum(L-1,Lx,Rx);
    }

4.3.2记录节点,现算现用

如果我们求的是排名呢?只有把所有的数据汇总到一起才能得到总排名,显然不能向上面那样对于每颗树单独算再相加.

假设我们已经得到了这(logn)颗线段树的和,现在我们要利用这个和线段树来计算答案.

容易发现,在每一个节点中,我们是进入左子节点还是右子节点,只与左子节点的大小与(K)的大小的关系有关(不知道为什么?回去看主席树求静态区间K小值),与树中其它任何节点都无关,这启发我们在要用到某个节点的数据的时候,再对这个节点求和.举个例子,现在我们在假想的和线段树中到了节点(u),需要通过(size[LC[u]])的大小来判断是进入左子树还是右子树,那么我们当场从那(logn)颗子树中揪出对应的(LC[u])这个节点,现场求和,并判断进入左子树还是右子树.

如果可以在(O(1))时间内揪出,显然复杂度也是(O(log_2^2n))的.

那么怎么个揪法呢?聪明的你一定可以想到,我们只需要在开始遍历这颗假想的和线段树之前,用一个数组存一下这(logn)颗线段树的根节点,即"应该揪出的节点的编号",然后每次进入左子树时,把"应该揪出的节点的编号"指向其左儿子,进入右子树则指向其右儿子.这样就可以保证(O(1))揪出了.

没看懂?再来看图片解释:

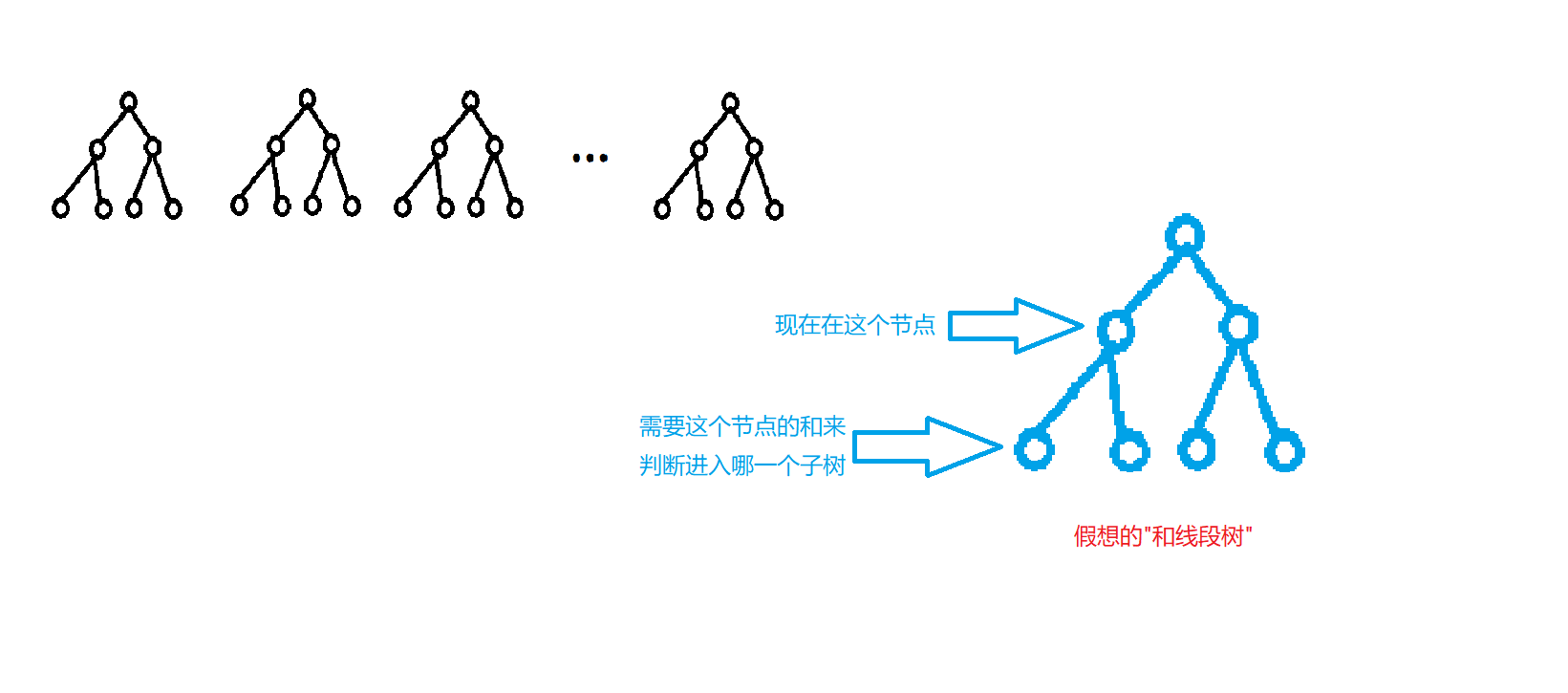
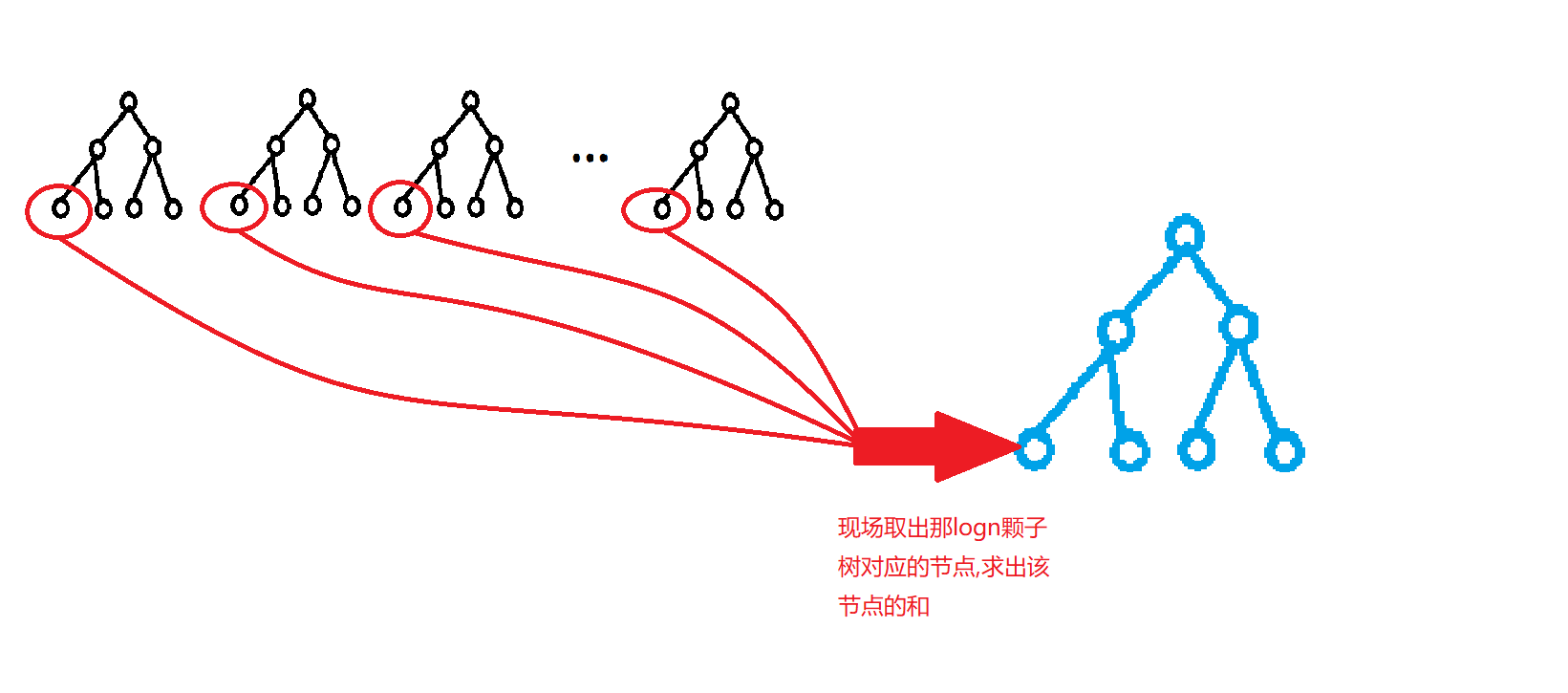
需要注意的是,我们现在求的是([L,R])区间,所以要进行现场加上(1...R)那(logn)颗子树和现场减去(1...L-1)那(logn)颗子树两步操作.

示例代码给出的是求区间(K)小值,显然我们可以把它延伸到求区间大于/小于(K)的值的个数的问题.

示例代码

    //内层线段树
	int Query(int L,int R,int K)
    {
        if(L==R)return L;
        int sum=0;
        for(int i=1;i<=C1;i++)sum-=v[LC[X[i]]];//现场减去1...L-1那logn颗子树
        for(int i=1;i<=C2;i++)sum+=v[LC[Y[i]]];//现场加上1...R那logn颗子树
 		if(K<=sum)//进入左子树
 		{
            for(int i=1;i<=C1;i++)X[i]=LC[X[i]];
            for(int i=1;i<=C2;i++)Y[i]=LC[Y[i]];
            return Query(L,Mid,K);	
        }
        else//进入右子树
 		{
            for(int i=1;i<=C1;i++)X[i]=RC[X[i]];
            for(int i=1;i<=C2;i++)Y[i]=RC[Y[i]];
            return Query(Mid+1,R,K-sum);				
        }
    } 
	//外层树状数组
    int Query(int L,int R,int K)
    {
        //预处理需要查询哪log(n)颗主席树 
        C1=C2=0;
        for(int i=(L-1);i;i-=(i&-i))X[++C1]=SegmentTree.Root[i];
        for(int i=R;i;i-=(i&-i))Y[++C2]=SegmentTree.Root[i];
        //"现算现用"查询区间K大 
        return SegTree.Query(1,n,K);
    }

4.3.3两种方法的比较

显然,离散化之后,值和排名是相等的,所以两种方法某种程度上是可以互相交换的.

5.例题

5.1 LG2617 Dynamic Rankings

带修改区间(K)小值模板题,按题意操作即可.示例代码采用了记录节点,现算现用的方法.

#include<cstdio>
#include<algorithm>
using namespace std;
#define SIZE 200005 

int n,m;
int nx;
int A[SIZE];//原数组 
//int B[SIZE];//离散化之后的数组
int Tem[SIZE];//离散化临时数组 
int X[SIZE];//计算第[1...L-1]颗主席树的和 需要累加的主席树的编号
int Y[SIZE];//计算第[1...R]颗主席树的和 需要累加的主席树的编号
int C1;//计算第[1...L-1]颗主席树的和 需要累加的主席树的数量
int C2;//计算第[1...R]颗主席树的和 需要累加的主席树的数量

//离散化 
void D()
{
    //for(int i=1;i<=n;i++)Tem[i]=A[i]; 
    sort(Tem+1,Tem+1+nx);
    nx=unique(Tem+1,Tem+1+nx)-(Tem+1);
    //for(int i=1;i<=n;i++)B[i]=lower_bound(Tem+1,Tem+1+nx,A[i])-Tem;
} 

//内层: 动态开点权值线段树
struct SegTreeX
{
    int Tot,Root[SIZE*400],v[SIZE*400],LC[SIZE*400],RC[SIZE*400];
    #define Mid ((L+R)>>1)
    void Change(int &x,int L,int R,int Pos,int Val)
    {
        if(x==0)x=++Tot;
        v[x]+=Val;
        if(L==R)return;
        if(Pos<=Mid)Change(LC[x],L,Mid,Pos,Val);
        else Change(RC[x],Mid+1,R,Pos,Val);
    }
    int Query(int L,int R,int K)
    {
        if(L==R)return L;
        int sum=0;
        for(int i=1;i<=C1;i++)sum-=v[LC[X[i]]];
        for(int i=1;i<=C2;i++)sum+=v[LC[Y[i]]];
 		if(K<=sum)
 		{
            for(int i=1;i<=C1;i++)X[i]=LC[X[i]];
            for(int i=1;i<=C2;i++)Y[i]=LC[Y[i]];
            return Query(L,Mid,K);	
        }
        else
 		{
            for(int i=1;i<=C1;i++)X[i]=RC[X[i]];
            for(int i=1;i<=C2;i++)Y[i]=RC[Y[i]];
            return Query(Mid+1,R,K-sum);				
        }
    } 
}SegTree;

//外层树状数组 
struct BITX
{
    void Change(int Pos,int Val)
    {
        int k=lower_bound(Tem+1,Tem+1+nx,A[Pos])-Tem;//离散化之后的权值 也就是权值线段树里的下标
        for(int i=Pos;i<=n;i+=i&(-i))SegTree.Change(SegTree.Root[i],1,nx,k,Val);
    }
    int Query(int L,int R,int K)
    {
        //预处理需要查询哪log(n)颗主席树 
        C1=C2=0;
        for(int i=(L-1);i;i-=(i&-i))X[++C1]=SegTree.Root[i];
        for(int i=R;i;i-=(i&-i))Y[++C2]=SegTree.Root[i];
        //"现算现用"查询区间K大 
        return SegTree.Query(1,nx,K);
    }
}BIT;

struct qq
{
    int opp,Lx,Rx,k;
}q[SIZE];

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){ scanf("%d",&A[i]); Tem[++nx]=A[i]; }
    char op[5];
    for(int i=1;i<=m;i++)
    {
        scanf("%s",op);
        if(op[0]=='Q'){ q[i].opp=1;	scanf("%d%d%d",&q[i].Lx,&q[i].Rx,&q[i].k); }
        else { scanf("%d%d",&q[i].Lx,&q[i].k); Tem[++nx]=q[i].k;}
    } 
    D();//离散化
    for(int i=1;i<=n;i++)BIT.Change(i,1);
    for(int i=1;i<=m;i++)
    {
        if(q[i].opp==1)
        {
            printf("%d
",Tem[BIT.Query(q[i].Lx,q[i].Rx,q[i].k)]);
        }
        else
        {
            BIT.Change(q[i].Lx,-1);
            A[q[i].Lx]=q[i].k;
            BIT.Change(q[i].Lx,1);
        }
    } 
    return 0;
}

5.2 [CQOI2011]动态逆序对

带删除的区间大于/小于(K)的值的个数的问题,采用了单独计算,累计答案的方法.

#include<cstdio>
const int SIZE=100005;
int n,m,A[SIZE],F[SIZE];
long long ans;

inline int In()
{
    char ch=getchar();
    int x=0;
    while(ch<'0'||ch>'9')ch=getchar();
    while(ch>='0'&&ch<='9'){ x=x*10+ch-'0'; ch=getchar(); }
    return x;
}

char Tem[100];
inline void Out(long long x)
{
    int Len=0;
    while(x){ Tem[++Len]=x%10+'0'; x/=10; }
    while(Len)putchar(Tem[Len--]);
    putchar('
');
}

//普通树状数组求初始逆序对
struct BIT
{
    long long C[SIZE];
    inline void change(int p,long long v){for(register int i=p;i<=n;i+=i&-i)C[i]+=v;}
    inline long long query(int p){long long x=0;for(register int i=p;i;i-=i&-i)x+=C[i];return x;}	
}T1;

//内层线段树 
struct Segtree
{
    int LC[SIZE*400],RC[SIZE*400],v[SIZE*400],Root[SIZE],Tot;
    void change(int &x,int L,int R,int Pos,int k)
    {
        if(x==0)x=++Tot;
        v[x]+=k;
        if(L==R)return;
        int Mid=(L+R)>>1;
        if(Pos<=Mid)change(LC[x],L,Mid,Pos,k);
        else change(RC[x],Mid+1,R,Pos,k);
    }
    int query(int x,int L,int R,int X,int Y)
    {
        if(x==0||L>Y||R<X)return 0;
        if(L>=X&&R<=Y)return v[x];
        int Mid=(L+R)>>1;
        return query(LC[x],L,Mid,X,Y)+query(RC[x],Mid+1,R,X,Y);
    }
}T2;

//外层树状数组
struct BITx
{
    inline void change(int p,int val,int v){ for(register int i=p;i<=n;i+=i&-i)T2.change(T2.Root[i],1,n,val,v); }
    inline int sum(int p,int Lx,int Rx){ int x=0;for(register int i=p;i;i-=i&-i)x+=T2.query(T2.Root[i],1,n,Lx,Rx);return x;}
    inline int query(int L,int R,int Lx,int Rx)
    {
        if(Lx>Rx||L>R)return 0;
        return sum(R,Lx,Rx)-sum(L-1,Lx,Rx);
    }
}T3;

int main()
{
    scanf("%d%d",&n,&m);
    for(register int i=1;i<=n;i++)
    {
        A[i]=In();
        ans+=T1.query(n)-T1.query(A[i]);
        T1.change(A[i],1);
        F[A[i]]=i;
    }
    for(register int i=1;i<=n;i++)T3.change(i,A[i],1);
    for(register int i=1;i<=m;i++)
    {
        Out(ans);
        int x=In();
        ans-=T3.query(1,F[x]-1,x+1,n);//在它前面又比它大
        ans-=T3.query(F[x]+1,n,1,x-1);//在它后面又比它小
        T3.change(F[x],x,-1); 
    }
    return 0;
}