Motivation:
深度度量学习的目标是学习一个嵌入空间来从数据点中捕捉语义信息。现有的成对或者三元组方法随着模型迭代过程会出现大量的平凡组导致收敛缓慢。针对这个问题,一些基于排序结构的损失取得了不错的结果,本文主要是针对排序loss存在的两个不足做的改进。
- 不足一:给定一个query,只利用了小部分的数据点来构建相似度结构,导致一些有用信息被忽略。本文给出的解决方案是把样本划分为正例集和负例集,目标是使得query离正例集比负例集近一个间隔。
- 不足二:此前方法都是在嵌入空间尽可能推进正样本的距离忽略了类内差异,作者使用一个超参来保留类内分布。

作者先是回顾了目前存在的一些loss, 从上图可以看到,ranked list loss也就是本文提出的方法,在训练中充分利用了输入样本信息。
本文的想法是把正例样本与负例样本以$m$隔开,类内样本允许存在$alpha-m$的分布差异,如下图所示:
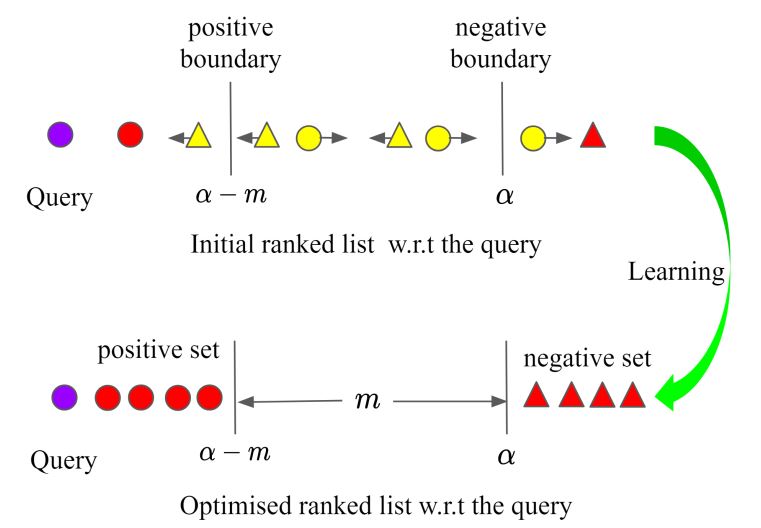
成对约束:
其基于成对损失,上图可以表示为:$L_{mathrm{m}}left(mathbf{x}_{i}, mathbf{x}_{j} ; f ight)=left(1-y_{i j} ight)left[alpha-d_{i j} ight]_{+}+y_{i j}left[d_{i j}-(alpha-m) ight]_{+}$。其中${x}_{i}$为query,$d_{i j}=left|fleft(mathbf{x}_{i} ight)-fleft(mathbf{x}_{j} ight) ight|_{2}$为样本间欧式距离,当$y_{i}=y_{j}$时,$y_{i j}=1$,反之为0。
对于每个query $mathbf{x}_{i}^{c}$,我们对gallery使用距离排序得到列表,其中存在$N_{c}-1$个正例点与$sum_{k eq c} N_{k}$个负例点。可以分别表示为$mathbf{P}_{c, i}=left{mathbf{x}_{j}^{c} | j eq i ight},left|mathbf{P}_{c, i} ight|=N_{c}-1$与$mathbf{N}_{c, i}=left{mathbf{x}_{j}^{k} | k eq c ight},left|mathbf{N}_{c, i} ight|=sum_{k eq c} N_{k}$。
难样本挖掘:
难样本挖掘因为收敛速度快,性能好被广泛使用,所谓难样本就是那些违反成对约束,loss值不为0的点。没有使用难样本挖掘在梯度融合时,这些信息量比较大的样本的贡献将被那些梯度为0的样本对削弱。所以我们先找出有贡献的样本。也就是:$mathbf{P}_{c, i}^{*}=left{mathbf{x}_{j}^{c} | j eq i, d_{i j}>(alpha-m) ight}$与$mathbf{N}_{c, i}^{*}=left{mathbf{x}_{j}^{k} | k eq c, d_{i j}<alpha ight}$。
基于损失的负样本挖掘:
对于每个query $mathbf{x}_{i}^{c}$,存在大量困难负样本,它们具有不同的损失值。为了更好的利用它们,作者提出基于损失值来加权负样本,也就是每个负样本违反约束的程度。加权策略可以公式化为:
$w_{i j}=exp left(T cdotleft(alpha-d_{i j} ight) ight), mathbf{x}_{j}^{k} in mathbf{N}_{c, i}^{*}$
作者注意到前面成对损失相对每个嵌入的梯度都是1.也就是:
$left|frac{partial L_{mathrm{m}}left(mathbf{x}_{i}, mathbf{x}_{j} ; f ight)}{partial fleft(mathbf{x}_{j} ight)} ight|_{2}=left|frac{fleft(mathbf{x}_{i} ight)-fleft(mathbf{x}_{j} ight)}{left|fleft(mathbf{x}_{i} ight)-fleft(mathbf{x}_{j} ight) ight|_{2}} ight|_{2}=1$
相对而言,作者提出来的则会被$w_{i j}$加权。$T$是一个温度因子,当T等于0时,就会退化为无困难负样本挖掘,当T趋近于无穷大,就会变成最困难负样本挖掘。
优化目标:
对于每个query $mathbf{x}_{i}^{c}$,优化的目标是让他离正例集合$mathbf{P}_{c, i}$比负例集合$mathbf{N}_{c, i}$的距离近$m$。同时,强迫所有的负样本离query的距离大于$alpha$。这样一来,其实所有的正例也被约束在离query距离$alpha-m$的范围内。对于正例集的约束如下:
$L_{mathrm{P}}left(mathbf{x}_{i}^{c} ; f ight)=frac{1}{left|mathbf{P}_{c, i}^{*} ight|} sum_{mathbf{x}_{j}^{c} in mathbf{P}_{c, i}^{*}} L_{mathrm{m}}left(mathbf{x}_{i}^{c}, mathbf{x}_{j}^{c} ; f ight)$
可以看到作者没有对正例进行加权,这是因为正样本很少。对困难负例的约束为:
$L_{mathrm{N}}left(mathrm{x}_{i}^{c} ; f ight)=sum_{mathbf{x}_{j}^{k} inleft[mathrm{N}_{c, i}^{*} ight]} frac{w_{i j}}{sum_{mathbf{x}_{j}^{k} inleft[mathrm{N}_{c, i}^{*} ight]}^{w_{i j}} L_{mathrm{m}}left(mathbf{x}_{i}^{c}, mathbf{x}_{j}^{k} ; f ight)}$
总体的损失便是两者的相加:$L_{mathrm{RLL}}left(mathbf{x}_{i}^{c} ; f ight)=L_{mathrm{P}}left(mathbf{x}_{i}^{c} ; f ight)+lambda L_{mathrm{N}}left(mathbf{x}_{i}^{c} ; f ight)$。在$mathbf{x}_{i}^{c}$的列表中,我们把其他样本的特征当作固定值,只有$f(mathbf{x}_{i}^{c})$会通过其他样本影响的加权和进行更新。
学习过程:

首先同样通过$P*K$的采样方式,也就是每批由$P$个人物,每个人物的$K$张图片组成。然后每张图片都被轮流当作query,剩下的就被当成gallery。可以公式化为:
$L_{mathrm{RLL}}(mathbf{X} ; f)=frac{1}{N} sum_{forall c, forall i} L_{mathrm{RLL}}left(mathbf{x}_{i}^{c} ; f ight)$
其中$N$为批大小,算法流程如下:
