@codeforces

目录

• @desription@
• @solution@
• @accepted code@
• @details@

---

@desription@

给定一个序列 a，定义它的权值 (c = sum_{i=1}^{n}a_i)。
你可以做如下的操作恰好一次：选择一个数，然后将它移动到一个位置（可以是原位置，序列开头与结尾）。
最大化序列权值。

input
第 1 行一个整数 n，表示序列长度（2 <= n <= 200000）。
第 2行 n 个整数 a1, a2, ..., an，表示这个序列（|ai| <= 1000000）。

output
输出一个整数，表示最大的序列权值。

sample input
4
4 3 2 5
sample output
39
sample explain
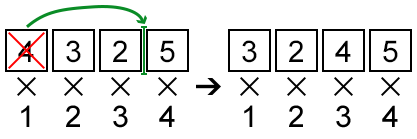
将 4 移动到 5 之前，得到 (c = 1*3 + 2*2 + 3*4 + 4*5 = 39)。

@solution@

移动可以向前移动也可以向后移动，我们仅考虑向后这一种，向前同理。

记原序列权值为 (c)，再记 (s[i]=sum_{p=1}^{i}a_p)。
考虑将第 i 号元素移动到第 j 个位置，则新序列权值为：

[c'=c-a[i]*i+a[i]*j+(s[j]-s[i]) ]

你看，它多么的斜率优化。

求最大值是上凸包，横坐标为 (-j)，从后往前是单增的。
但是……斜率为 (a[i])，是不单调的。
所以我们必须在凸包上作二分寻找答案。

一开始我很懵逼，凸包不应该是三分求极值吗？后来我才发现，二分原来是二分斜率。凸包上斜率是单增的，所以可以使用二分。（但是三分好像也可以……只是大概没人想写而已……明明三分更容易调错来着 qwq）。

二分找什么呢？就是找到一个点，它和它前驱的斜率大于等于 (a[i])，它和它后继的斜率小于等于 (a[i])。

注意二分常见的错误：边界。

@accepted code@

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 200000;
int n;
ll a[MAXN + 5], s1[MAXN + 5], s2[MAXN + 5];
ll c1(int i) {return s1[n] - a[i]*i + s2[i-1];}
ll c2(int i) {return s1[n] - a[i]*i + s2[i];}
ll k1(int i) {return -a[i];}
ll k2(int i) {return a[i];}
ll x1(int j) {return j;}
ll x2(int j) {return -j;}
ll y1(int j) {return -s2[j-1];}
ll y2(int j) {return -s2[j];}
int stk[MAXN + 5], tp;
double slope1(int p, int q) {return 1.0*(y1(p) - y1(q))/(x1(p) - x1(q));}
double slope2(int p, int q) {return 1.0*(y2(p) - y2(q))/(x2(p) - x2(q));}
int main() {
	scanf("%d", &n);
	for(int i=1;i<=n;i++)
		scanf("%lld", &a[i]);
	for(int i=1;i<=n;i++) {
		s1[i] = s1[i-1] + a[i]*i;
		s2[i] = s2[i-1] + a[i];
	}
	ll ans = -(1LL<<62); tp = 0;
	for(int i=1;i<=n;i++) {
		while( tp > 1 && slope1(stk[tp - 1], stk[tp]) <= slope1(stk[tp], i) )
			tp--;
		stk[++tp] = i;
		int le = 1, ri = tp;
		while( le < ri ) {
			int mid = (le + ri) >> 1;
			if( slope1(stk[mid], stk[mid+1]) <= k1(i) ) ri = mid;
			else le = mid + 1;
		}
		ans = max(ans, c1(i) + y1(stk[le]) - k1(i)*x1(stk[le]));
	}
	tp = 0;
	for(int i=n;i>=1;i--) {
		while( tp > 1 && slope2(stk[tp - 1], stk[tp]) <= slope2(stk[tp], i) )
			tp--;
		stk[++tp] = i;
		int le = 1, ri = tp;
		while( le < ri ) {
			int mid = (le + ri) >> 1;
			if( slope2(stk[mid], stk[mid+1]) <= k2(i) ) ri = mid;
			else le = mid + 1;
		}
		ans = max(ans, c2(i) + y2(stk[le]) - k2(i)*x2(stk[le]));
	}	
	printf("%lld
", ans);
}

@details@

一开始我从前往后和从后往前都用同一个横坐标，然后因为枚举顺序不一样，导致一个是单增的一个是单减的。
单增的还好，单减的那个让我二分时各种边界错误……调到死都调不出来……
最后索性把单减那个横坐标取个相反数，变成单增的。然后一遍过 =_=。