Java 数据结构

Java 数据结构 - 队列

目录

• Java 数据结构 - 队列
  • 1. 什么是队列
    • 1.1 队列的主要特性
    • 1.2 队列的相关概念
  • 2. 复杂度分析
    • 2.1 链式队列
    • 2.2 顺序队列
    • 2.3 循环队列
    • 2.4 阻塞队列和并发队列
  • 3. 队列在软件工程中应用

数据结构与算法目录(https://www.cnblogs.com/binarylei/p/10115867.html)

我们今天要讲的数据结构是队列，比如 Java 线程池任务就是队列实现的。

1. 什么是队列

和栈一样，队列也是一种操作受限的线性结构。使用队列时，在一端插入元素，而在另一端删除元素。

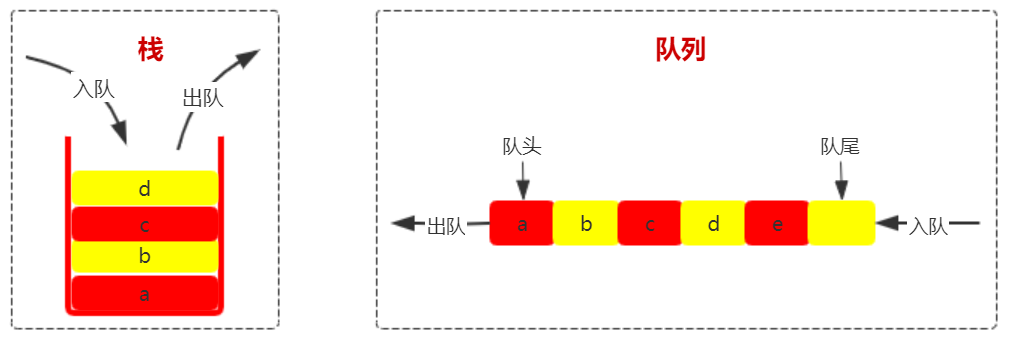
1.1 队列的主要特性

• 队列中的数据元素遵守 "先进先出"（First In First Out）的原则，简称 FIFO 结构。
• 限定只能在队列一端插入，而在另一端进行删除操作。

1.2 队列的相关概念

• 入队（enqueue）：队列的插入操作。
• 出队（dequeue）：队列的删除操作。

2. 复杂度分析

和栈一样，队列也有两种实现方案，我们简单分析一下这两种队列的复杂度：

• 动态队列（链表）：也叫链式队列。其插入、删除时间复杂度都是 O(1)。
• 静态队列（数组）：也叫顺序队列。当队列队尾指针移到最后时，此时有两种操作：一是进行简单的数据搬移，二是进行队列循环。

关于队列的实现，我们只实现如下的基本操作。

public interface Queue {
    Queue enqueue(Object obj);   // 入队
    Object dequeue();            // 出队
    int size();                  // 元素个数
}

2.1 链式队列

链式队列的实现非常简单，其插入和删除的时间复杂度都是 O(1)。为了简化代码的实现，我们引入哨兵结点。如下图所示，head 头结点是哨兵结点，不保存任何数据，从 head.next 开始保存数据，tail 结点指向最后一个元素结点。链表队列头结点和尾结点说明：

• 头结点：head 结点为哨兵结点，不保存任何数据，数据从第二个结点开始。
• 尾结点：tail 结点指向最后一个数据结点。

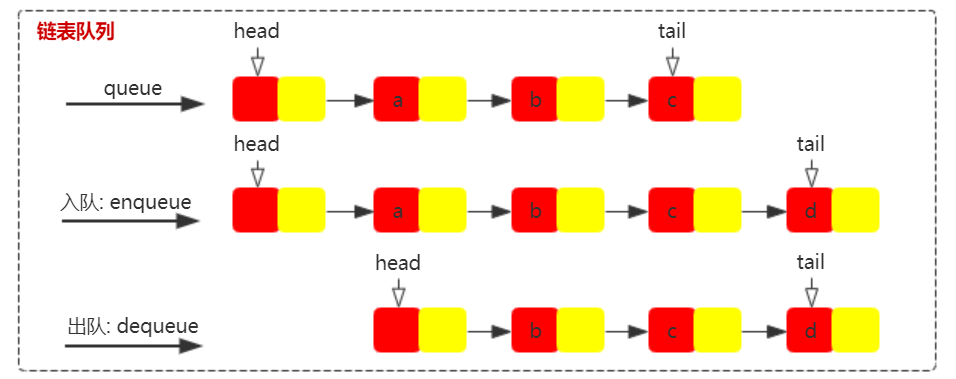
根据上图，我们可以轻松实现一个链表组成的队列，代码也很简单。

public class LinkedQueue implements Queue {

    private Node head;
    private Node tail;
    private int size;

    public LinkedQueue() {
        head = new Node(null, null);
        tail = head;
    }

    @Override
    public Queue enqueue(Object obj) {
        tail.next = new Node(obj, null);
        tail = tail.next;
        size++;
        return this;
    }

    @Override
    public Object dequeue() {
        Node next = head.next;
        if (next == null) {
            return null;
        }
        head = head.next;
        size--;
        return next.item;
    }

    @Override
    public int size() {
        return size;
    }

    public static class Node {
        private Object item;
        private Node next;

        public Node(Object item, Node next) {
            this.item = item;
            this.next = next;
        }
    }
}

2.2 顺序队列

如果是数组实现的队列，则比链表要复杂一些，当尾结点指向数组的最后一个位置时，没有剩余的空间存放数据时，此时该如何处理？通过我们有两种解决方案：

• 数据搬移：将 head ~ tail 结点的数据搬移到从 0 结点开始。
• 循环队列：tail 结点从 0 开始循环使用，不用搬移数据。

我们先看一下循环队列

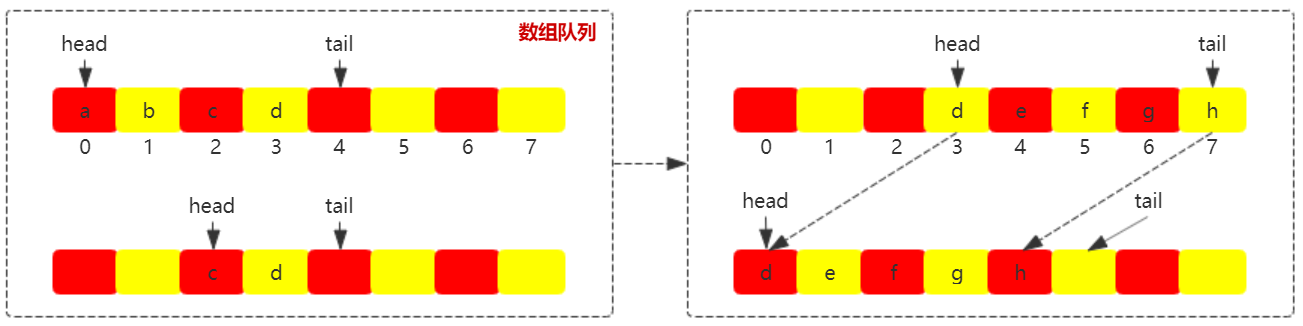
如上图所示，当尾结点指向数组最后一个位置，当 tail 指向数组最后位置时，触发数据搬移，将 head ~ tail 结点的数据搬移到从 0 结点开始。数组队列头结点和尾结点说明：

• 头结点：head 结点指向第一个数据结点。当 head == tail 时说明队列处于队空状态，直接返回 null。
• 尾结点：tail 结点指向最后一个数据之后的空结点。当 tail == capcity 时说明队列处于队满状态，需要扩容或进行数据搬移。

根据上述理论代码实现如下：

public class ArrayQueue implements Queue {

    private Object[] array;
    private int capcity;
    // head指向第一个数据结点的位置，tail指向最后一个数据结点之后的位置
    private int head;
    private int tail;

    public ArrayQueue() {
        this.capcity = 1024;
        this.array = new Object[this.capcity];
    }

    public ArrayQueue(int capcity) {
        this.capcity = capcity;
        this.array = new Object[capcity];
    }
    
    /**
     * tail 指向数组最后位置时，需要触发扩容或数组搬移
     * 1. head!=0 说明数组还有剩余的空间，将 head 搬运到队列 array[0]
     * 2. head==0  说明数组没有剩余的空间，扩容
     */
    @Override
    public Queue enqueue(Object obj) {
        if (tail == capcity) {
            if (head == 0) {
                resize();
            } else {
                rewind();
            }
        }
        array[tail++] = obj;
        return this;
    }

    @Override
    public Object dequeue() {
        if (head == tail) {
            return null;
        }
        Object obj = array[head];
        array[head] = null;
        head++;
        return obj;
    }
    
    // 将 head 搬运到队列 array[0]
    private void rewind() {
        for (int i = head; i < tail; i++) {
            array[i - head] = array[i];
            array[i] = null;
        }
        tail -=  head;
        head = 0;
    }

    // 扩容
    private void resize() {
        int oldCapcity = this.capcity;
        int newCapcity = this.capcity * 2;
        Object[] newArray = new Object[newCapcity];
        for (int i = 0; i < oldCapcity; i++) {
            newArray[i] = array[i];
        }
        this.capcity = newCapcity;
        this.array = newArray;
    }
    
    @Override
    public int size() {
        return tail - head;
    }
}

说明： 数组队列出队的时间复杂度始终是 O(1)。但入队时要分为三种情况：

• 有空间：大多数情况，也是最好时间复杂度 O(1)。
• 没有空间需要数据搬移：执行 n 后触发一次数据搬移，最坏时间复杂度 O(n)。
• 没有空间需要扩容：执行 n 后触发一次数据搬移，最坏时间复杂度 O(n)。

如果采用摊还分析法，最好时间复杂度 O(1)，最坏时间复杂度 O(n)，摊还时间复杂度为 O(1)。虽然，平均时间复杂度还是 O(1)，但我们能不能不进行数据搬移，直接循环使用数组呢？

2.3 循环队列

循环队列是一种非常高效的队列，我们需要重点掌握它，要能轻松写出无 BUG 的循环队列。

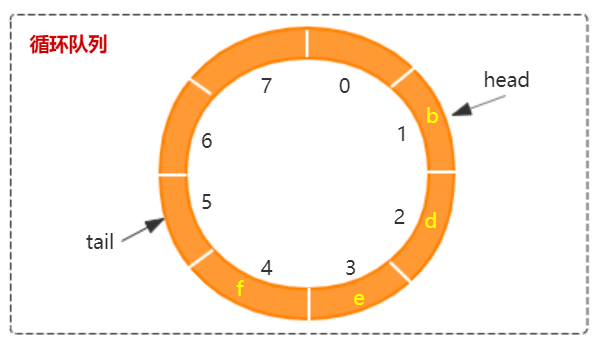
数组队列头结点和尾结点说明：

• 头结点：head 结点指向第一个数据结点。当 head == tail 时说明队列处于队空状态，直接返回 null。否则在元素出队后，需要重新计算 head 值。
• 尾结点：tail 结点指向最后一个数据之后的空结点。每次插入元素后重新计算 tail 值，当 tail == head 时说明队列处于队满状态，需要扩容。
• 元素位置：对数组长度取模 (tail + 1) % length ，所以这种数据为了提高效率，都要求数组长度为 2^n，通过位运算取模 (tail + 1) & (length - 1)。

public class ArrayCircularQueue implements Queue {

    private Object[] array;
    private int capcity;
    // 头结点指向
    private int head;
    private int tail;

    public ArrayCircularQueue() {
        this.capcity = 1024;
        this.array = new Object[this.capcity];
    }

    public ArrayCircularQueue(int capcity) {
        this.capcity = capcity;
        this.array = new Object[capcity];
    }

    @Override
    public Queue enqueue(Object obj) {
        array[tail] = obj;
        if ((tail = (tail + 1) % capcity) == head) {
            resize();
        }
        return this;
    }

    @Override
    public Object dequeue() {
        if (head == tail) {
            return null;
        }
        Object obj = array[head];
        array[head] = null;
        head = (head + 1) % capcity;
        return obj;
    }

    // 不扩容，要先判断能否往数组中添加元素
    public Queue enqueue2(Object obj) {
        if ((tail + 1) % capcity == head) return this;
        array[tail] = obj;
        tail = (tail + 1) % capcity;
        return this;
    }

    // 扩容
    private void resize() {
        // 说明还有空间
        if (head != tail) {
            return;
        }
        int oldCapcity = this.capcity;
        int newCapcity = this.capcity * 2;
        Object[] newArray = new Object[newCapcity];
        for (int i = head; i < oldCapcity; i++) {
            newArray[i - head] = array[i];
        }
        for (int i = 0; i < head; i++) {
            newArray[capcity - head + i] = array[i];
        }
        this.capcity = newCapcity;
        this.array = newArray;
        this.head = 0;
        this.tail = oldCapcity;
    }


    @Override
    public int size() {
        return tail - head;
    }
}		

说明： 循环队列关键是判断队空和空满的状态分别进行处理。除开扩容操作，循环队列的入队和出队的时间复杂度都是 O(1)，同时也可以充分利用 CPU 缓存，所以说一种高效的数据结构。

2.4 阻塞队列和并发队列

3. 队列在软件工程中应用

如 JDK 线程池，当线程池没有空闲线程时，新的任务请求线程资源时，线程池该如何处理？各种处理策略又是如何实现的呢？我们一般有两种处理策略。

1. 非阻塞的处理方式，直接拒绝任务请求；
2. 阻塞的处理方式，将请求排队，等到有空闲线程时，取出排队的请求继续处理。

---

每天用心记录一点点。内容也许不重要，但习惯很重要！