Codeforces 476C. Dreamoon and Sums

Dreamoon loves summing up something for no reason. One day he obtains two integers a and b occasionally. He wants to calculate the sum of all nice integers. Positive integer x is called nice if 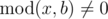 and 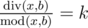, where k is some integer number in range [1, a].

By  we denote the quotient of integer division of x and y. By  we denote the remainder of integer division of x and y. You can read more about these operations here: http://goo.gl/AcsXhT.

The answer may be large, so please print its remainder modulo 1 000 000 007 (109 + 7). Can you compute it faster than Dreamoon?

Input

The single line of the input contains two integers a, b (1 ≤ a, b ≤ 10^7).

Output

Print a single integer representing the answer modulo 1 000 000 007 (10^9 + 7).

设x = k1b + k2

那么可以得到 k1 = kk2

所以 x = kk2b + k2 

就是求出所有x的和

已知k2范围,b,k范围，简单的求和

PS:最近开始用Python练习

a = input()
a = a.split()
a,b = int(a[0]),int(a[1])

k2 = b*(b-1)*a // 2 
k = (b-1)*b//2 * b* (1+a)*a // 2
res = (k + k2) % 1000000007
print(res)