一旦在一个多边形中找到了一个交点,就可以执行许多其他操作。如果多边形被分配了颜色模式,则必须检索交点处的颜色。类似的操作必须对其他纹理映射过程执行,比如bump映射。如果多边形是曲面上的一条路径,则必须从顶点的不同法线推导出精确法线。
本节将介绍在凸四边形中获取点位置的算法,因为这种形状在各种应用中经常使用。通过算法计算参数值(u,v)。这个坐标对表示点相对于四条边的位置,作为从0到1的坐标轴对。问题如图9所示。
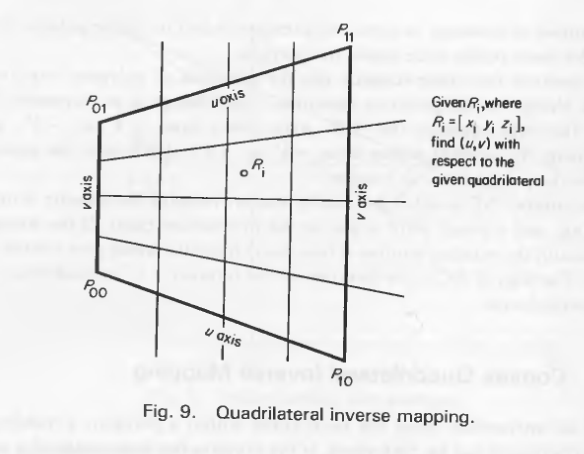
注意,映射本身也可以用作内外测试。如果点在四边形之外,计算出的(u,v)对将落在(0…1,0…1)范围之外。
从四边形的平面上的一个交点开始。
用四个点来定义凸四边形:

这些点定义u和v的轴,例如(P00,P10)定义了v=0时的u轴。平面的法线(不需要规范化)称为Pn。
推导过程是相当复杂的,因此不包含在本讨论中。在[15]中有完整内容。插值必须计算许多因素。这些因素分为两类:点平面相关和平面相关。那些与平面有关的可以(而且应该)提前计算并传递给算法,除非它们是其他的限制因素,比如内存空间。这些平面相关的因素分别为:
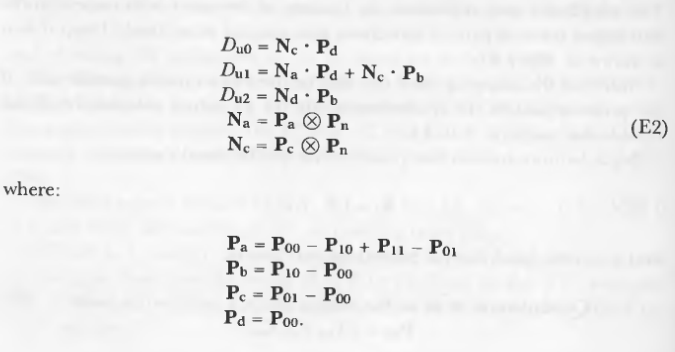
基本思想是为u定义一个函数,描述垂直平面(由u和四边形的坐标轴定义)与坐标系原点的距离:
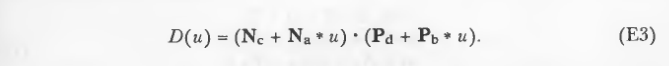
(E2)中计算的因子用于表示这个平面相关方程。 给定ri,包含这一点的垂直平面的距离为:
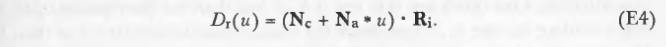
设D(u) = Dr(u),解u,化简:
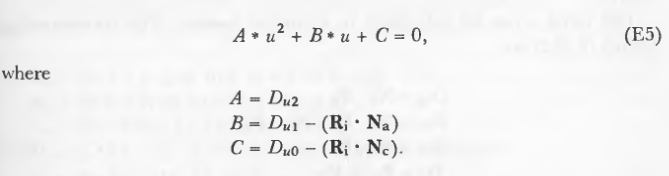
这只是一个二次方程,它的解是直截了当的,因此不会被显示出来。为了获得更高的效率,一些其他因素对于每一个四边形和存储都值得一次计算。注意,只有当Du2!=0时才可以计算这些值。这些因素是:
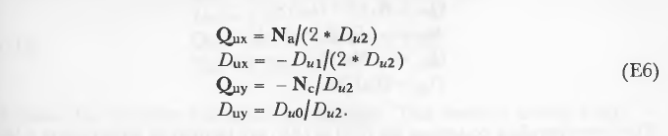
用(E2)和(E6)中的九个因子可以计算出u的值。 该解决方案有两种形式,取决于u轴是否平行。 通过以下条件确定轴是否平行:
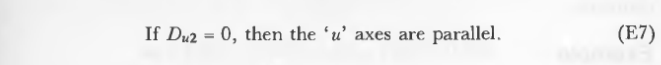
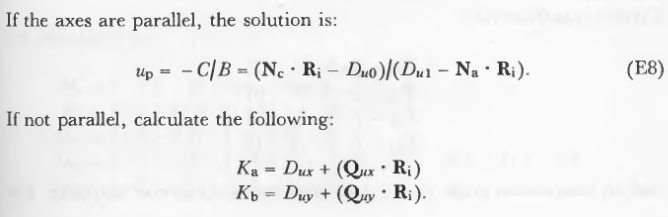
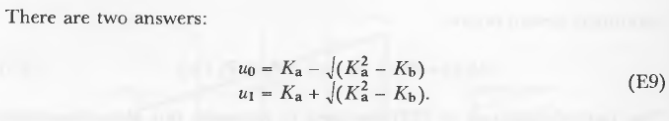
这两个中最多只有一个值位于范围(0 ... 1)内,那是有用的值。 如果最终的u值不在(0..1)中,则该点在四边形之外。 一个快速测试是测试Ka是否小于判别式(德尔塔)。 如果不是,则计算u0,否则为u1。 然后检查最终的u值,看它是否小于1.不是如果u0和u1都在有效范围内,那么四边形不是凸的。
值v可以用类似的方式计算。 (E2)的相应因子是:
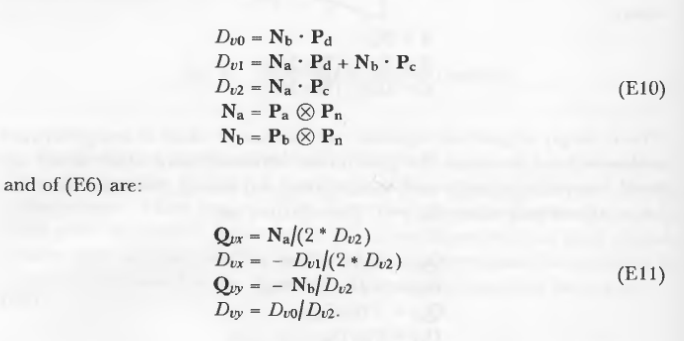
(E7)至(E9)的相应方程式是通过用v代替u并用Nb代替Nc形成的。
依赖于点平面的过程本身所需的计算是按照u或v值,8个加法/减法,7个乘法,1个平方根和4个比较。
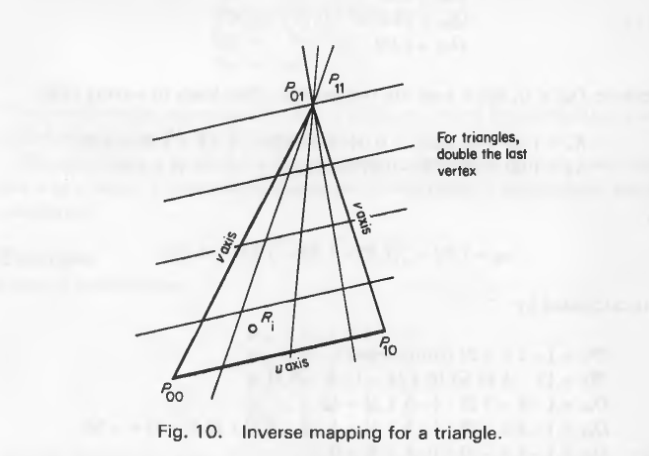
三角形逆映射
逆映射也可以应用于三角形。 一种技术是将三角形传递给算法,将最后一个顶点加倍,以便为例程提供四点支持。 例如,如果标准程序按照P00,P10,P11,P01的顺序接受四边形的点,则P01再次发送三角形的最后点P11。 在这种情况下,(u,v)的映射将如图10所示,u轴定义为平行。
当要映射的点位于加倍的顶点时会发生特殊情况。 在这个顶点,一个参数的所有值收敛。 在例子中,在图10中的P11处,所有的u值都是正确的。 由于这个奇点没有正确的答案,我们可以选择将其视为多边形之外的无效点,或者可以将其指定为任意值(零点可能是候选)。 通过检查方程(E8)中的除数是否等于零来测试这种特殊情况。