HMM

HMM（Hidden Markov Model）

相关概念

时序数据（Non-Sequential Data） vs 非时序数据（Sequential Data）

时序数据：文本、天气（长度不固定）

时序模型：HMM、CRF、RNN、LSTM

背景介绍

马尔可夫过程

概念：大概的意思就是未来只与现在有关，与过去无关。

无后效性=马尔科夫性：下一时刻的状态只与当前状态有关，与上一时刻状态无关

马尔可夫过程：具有马尔科夫性的过程

数学公式表示：

设有一个随机过程X（t），如果对于下一个任意的时间序列 ,在给定随机变量 的条件下， 的分布可表示为 则称为马尔可夫过程或者简称马氏过程。

转移分布函数：

转移概率：

马尔可夫链

概念：是最简单的马氏过程，即时间和状态过程的取值参数都是离散的马尔可夫过程。

n次达到转移概率：即通过n次达到目标状态

[P_{ij}^n = P[{X_{n+m}=j|X_m=i}] ]

表示当前（第m步）的状态为i，经过n步转移后（第n+m步）系统的状态为j的概率

---

例子：设有三个黑球和三个白球，把这六个球任意分给甲乙两人，并把甲拥有的白球数定义为该过程的状态，则有四种状态0,1,2,3。现每次从甲乙双方各取一球，然后相互交换。经过n次交换后过程的状态记为Xn，试问该过程是否是马氏链？如是，试计算其一步转移概率矩阵。

解：由题意知，甲拥有白球的状态为离散值，且当前状态仅与上一时刻状态有关。所以这个过程是马氏链。

由于六个球任意分给甲、乙两人，所以根据甲拥有球的数量不同而状态不同。

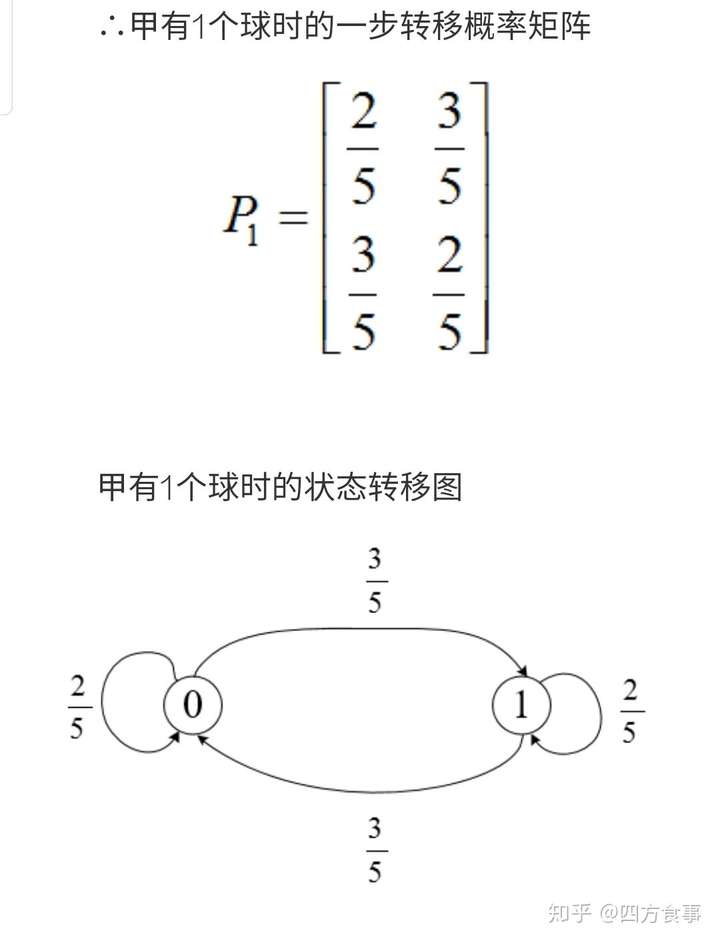
情况一：甲有1个球，则甲的状态有2种：0和1。

①甲当前状态为0，则说明甲有1个黑球，乙有2个黑球和3个白球，交换一次后

甲状态为0的概率：2/5

甲状态为1的概率：3/5

②甲当前状态为1，则说明甲有1个白球，乙有3个黑球和2个白球，则交换一次后

甲状态为0的概率：3/5

甲状态为1的概率：2/5

HMM模型介绍

生成模型 + latent模型

隐马尔可夫模型是统计模型，用于描述一个含有隐变量的马尔科夫过程。马尔可夫过程+隐藏的状态的统计马尔可夫模型。

隐马尔科夫链HMM三个重要假设：

1. 当前观测值只由当前隐藏状态确定，而与其他隐藏状态或观测值无关（隐藏状态假设）

2. 当前隐藏状态由其前一个隐藏状态决定（一阶马尔科夫假设）

3. 隐藏状态之间的转换函数概率不随时间变化（转换函数稳定性假设）

例子：掷骰子，挑到每个骰子的概率都为1/3。例如我们可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4。

可见状态链：1 6 3 5 2 7 3 5 2 4

隐含状态链（可能为）：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8

转换概率：1/3，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

输出概率：隐含状态和可见状态之间有一个概率叫做输出概率（emission probability）。就我们的例子来说，六面骰（D6）产生1的输出概率是1/6。产生2，3，4，5，6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。

HMM的模型参数（离散）

[ heta = (A,B,pi) ]

如上例的输出概率b，转换概率a

HMM两个主要任务

1. 给定模型的参数θ,找合适的Z

2. 估计模型参数θ：

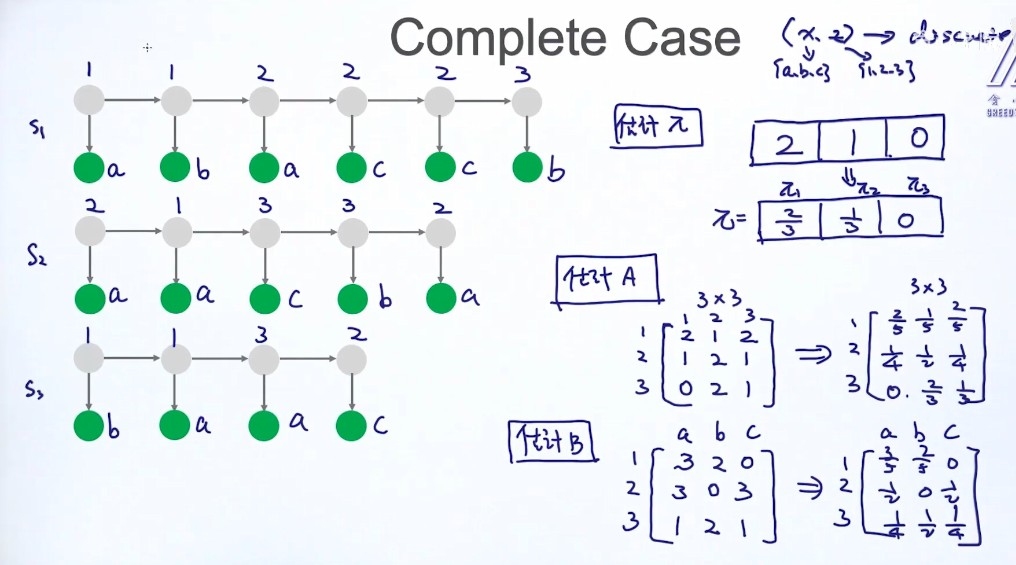
   • complete case：(X,Z)

   • Incomplete case：(X,{部分z}) + EM

任务1：求Z （即解码问题，用于预测）

• 解法1：直接计算法：

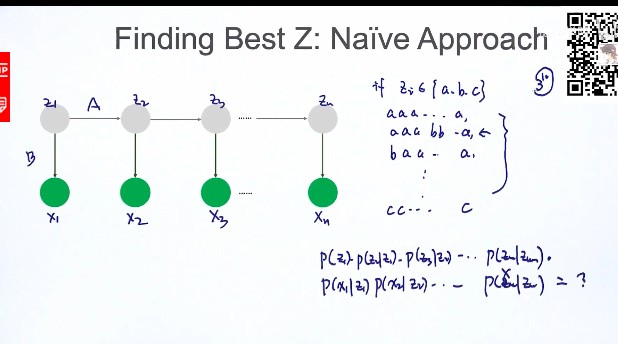
• 解法2：Viterbi：Finding Best Z

  动态规划，把原来问题变成子问题。关键在构造子问题。选择最优的路径

  

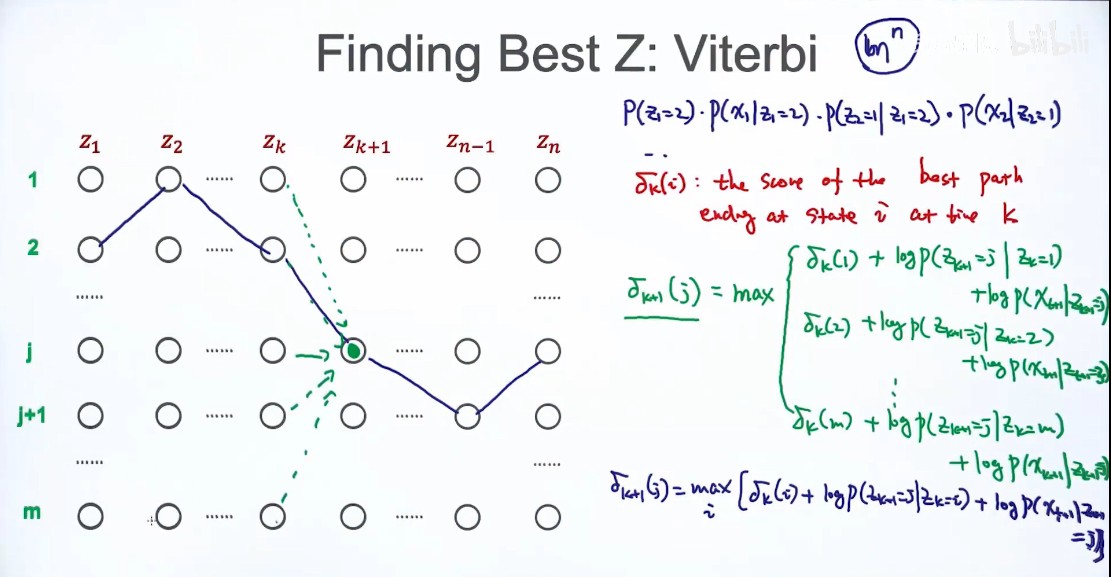
  条件：z只和前后的变量有联系

任务2：估计θ

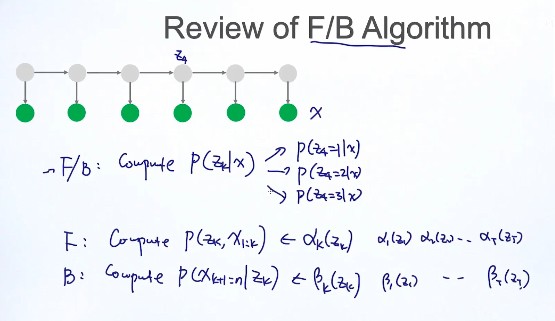
• F/B算法：complete$ P(z_k|x)$

  [P(z_k,x) = P(x_{k+1}...x_n|z_k,x_1...x_k)*p(z_k,x_1...x_k)\ = p(x_{k+1}...x_n|z_k)*p(z_k,x1...x_k) ]
  [P(z_k|x) = frac{P(z_k,x)}{p(x)} ]

• Forward 算法：complete$ P(z_k,x1...x_k)$

  [p(z_k,x_1...x_k) = [ ]p(z_{k-1},x_1...x_{k-1}) ......动态规划 ]

  左边和右边的变量不同，$ z_k$ ， (z_{k-1}),将(z_{k-1})边缘化

  [p(z_k,x_1...x_k) = sum_{z_{k-1}}p(z_{k-1},z_k,x_1...x_k)\ sum_{z_{k-1}}p(z_{k-1},x_1...x_{k-1})*p(z_k|z_{k-1},x_1...x_{k-1})*p(x_k|z_k,z_{k-1},x_1...x_{k-1}) ]

  D-sepretion:条件独立(p(z_k|z_{k-1},x_1...x_{k-1}) = p(z_k|z_{k-1}))

  (p(x_k|z_k,z_{k-1},x_1...x_{k-1}) = p(x_k|z_k))

  [p(z_k,x_1...x_{k-1}) =sum_{z_{k-1}}p(z_{k-1},x_1...x_{k-1})*p(z_k|z_{k-1})*p(x_k|z_k) ]

• Backward 算法：complete (P(x_{k+1}...x_n|z_k))

[p(x_{k+1}|z_k) = []P(x_{k+1}) ]

[p(x_{k+1}...x_n|z_k) = sum_{z_{k+1}}p(x_{k+1}...x_n,z_{k+1}|z_k)\ =sum_{k+1}p(x_{k+2}...x_n|z_{k+1},z_k,x_{k+1})*p(x_{k+1}|z_{k+1},z_n)*p(z_{k+1}|z_k)\ sum_{z_{k+1}}p(x_{k+2}...x_n|z_{k+1})p(x_{k+1}|z_{k+1})P(z_{k+1}|z_k) ]

FB的作用：

1. FB --> 模型参数
2. change detection

• incomplete case：只知道X，未知Z

情况1：Complete case

情况2：Incomplete case

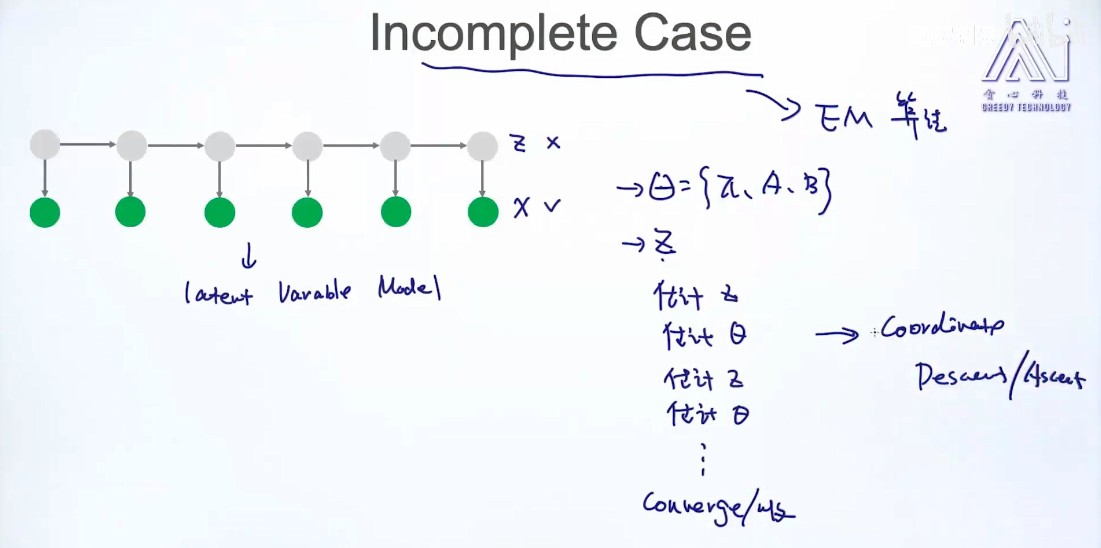
• 求z

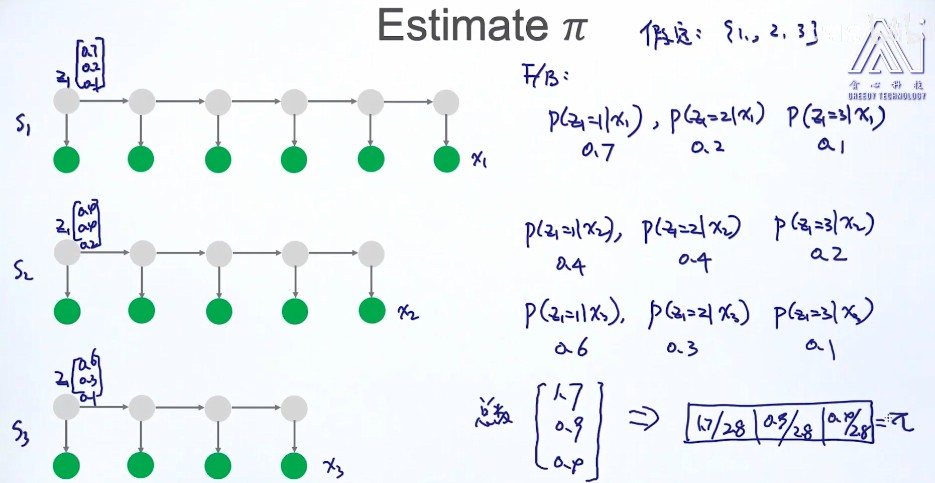
• 求(pi)

求的是期望的次数

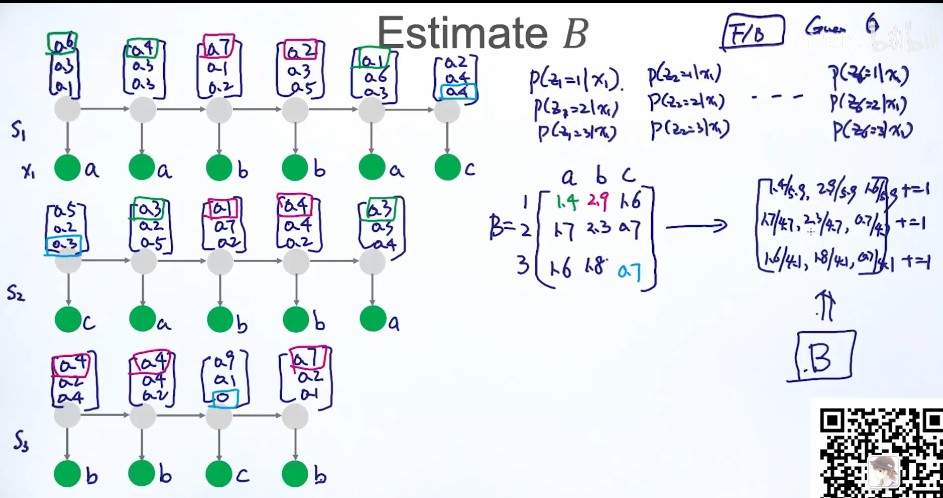
• 求B，状态 --> 观测值

HMM解决的三种问题

• 例9子中的概述：

  预测问题：知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道每次掷出来的都是哪种骰子（隐含状态链）。

  概率估计问题：还是知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道掷出这个结果的概率。

  学习问题：知道骰子有几种（隐含状态数量），不知道每种骰子是什么（转换概率），观测到很多次掷骰子的结果（可见状态链），我想反推出每种骰子是什么（转换概率）

应用篇

HMM的目标是要恢复一个数据序列，可不立即被观察到的（但其他数据依赖上述数据）

在NLP主要有：

• 词性标注：给定一个词的序列（也就是句子），找出最可能的词性序列（标签是词性），如ansj分词和ICTCLAS分词等。
• 分词：给定一个字的序列，找出最可能的标签序列（断句符号：[词尾]或[非词尾]构成的序列）。结巴分词目前就是利用BMES标签来分词的，B（开头），M（中间），E（结尾），S（独立成次）
• 命名实体识别：给定一个词的序列，找出最可能的标签序列（内外符号：[内]表示词属于命名实体，[外]表示不属于）。如ICTCLAS实现的人名识别、翻译人名识、地名识别都是用同一个Tagger实现的。
• 机器翻译

参考：https://zhuanlan.zhihu.com/p/86995916

https://www.cnblogs.com/skyme/p/4651331.html

https://www.bilibili.com/video/BV1ik4y167kr?from=search&seid=14006835468249013411

系列文章：https://blog.csdn.net/tostq/category_6103895.html