1. 困难问题与简单问题
生活中:没有具体的量化标准
计算机:时间复杂度(大O表示法)
2. 什么是P,NP,NP Complete
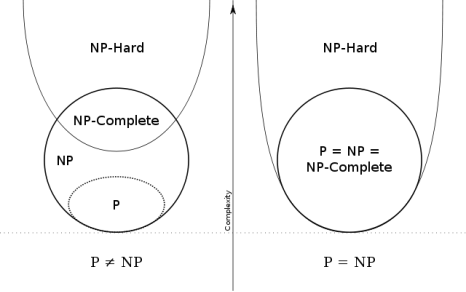
(一)P = Polynomial (在多项式时间内得到解决)
(二)NP = Non Deterministic Polynomial (对于一个问题,假如能在多项式时间内验证这个解是否为正确解,那么这个问题就是NP问题)
(三)NP Complete:NPC问题是NP问题的一个子集。(假如一个问题是NP问题,可在多项式时间内得到解决,但暂时无法在P时间内解决)
SAT:Boolean Satisfiability problem
|
现在我们有一系列布尔变量,x1 x2 x3 ... xn(为True或者False) CNF的算式(令n=5): (x1 ||x4 ||x5)&&(x2||!x3||x2)&&(x2||!x3||!x4)... 有没有一种组合x1 .... x5, 使得最终结果为True 是否为NP问题? 有没有可能在多项式时间内求出问题的解呢? |
3. 千禧难题:P = NP?
P = NP 我们相信“暂时没能在多项式时间内解决的,以后都能够解决”
|
判断和求解属于同一级别的难度? 分辨音乐好听还是难听VS作一首好听的曲子 分辨一道菜好吃还是不好吃VS做得一手好菜 分辨一本书好不好看VS写一本好书 |
P = NP的意义
4. NP complete问题的特性
问题可以相互约化(Reducibility,多项式时间内转化)
Clique problem(在图中找全连接+) 和SAT
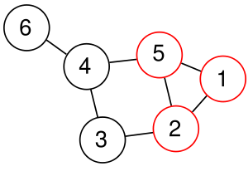
Independent Set
Vertex Cover
Edge Cover
5. NP Complete问题的处理策略
(一)对问题施加限制(增加条件)
(二)改进指数时间算法(2^n -> 1.5^n)
(三)启发示方法
回溯法(是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为“回溯法”,而满足回溯条件的某个状态的点称为“回溯点”)
局部搜索(局部搜索算法从一个初始解开始,通过邻域动作,产生其邻居解,判断邻居解的质量,根据某种策略,来选择邻居解,重复上述过程,至到达终止条件,容易陷入局部最优)
随机游动
模拟退火(为了防止陷入局部最优,模拟退火算法以一定概率接受比当前解差的解,接受差解的概率随着迭代次数的增加而下降,或者说是随着温度T的下降而下降)
遗传算法( 模拟物竞天择的生物进化过程,通过维护一个潜在解的群体执行了多方向的搜索,并支持这些方向上的信息构成和交换)
|
小故事 为了找出地球上最高的山,一群有志气的兔子们开始想办法。 兔子朝着比现在高的地方跳去。他们找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是Iterative Improvement,它不能保证局部最优值就是全局最优值。 兔子喝醉了,它随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,它渐渐清醒了并朝最高方向跳去。这就是模拟退火。 兔子们知道一个兔的力量是渺小的。它们互相转告着,哪里的山已经找过,并且找过的每一座山他们都留下一只兔子做记号。他们制定了下一步去哪里寻找的策略。这就是禁忌搜索。 兔子们吃了失忆药片,并被发射到太空,然后随机落到了地球上的某些地方。他们不知道自己的使命是什么。但是,如果你过几年就杀死一部分海拔低的兔子,多产的兔子们自己就会找到珠穆朗玛峰。这就是遗传算法。 |
6. 总结
P Problem: 对于任意的输入规模n,问题都可以在n的多项式时间内得到解决
NP(Non-deterministic Polynomial) Problem: 可以在多项式的时间里验证一个解的问题
NPC(Non-deterministic Polynomial Complete) Problem: 满足两个条件 (1)是一个NP问题 (2)所有的NP问题都可以约化到它
NP-Hard Problem: 满足NPC问题的第二条,但不一定要满足第一条
7. 参考资料
https://people.orie.cornell.edu/dpw/orie6300/Lectures/lec25.pdf
http://www.doc88.com/p-2778214890655.html
https://wenku.baidu.com/view/8a88fa54e418964bcf84b9d528ea81c758f52ed5.html?rec_flag=default&sxts=1563369616572
https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-046j-design-and-analysis-of-algorithms-spring-2012/lecture-notes/MIT6_046JS12_lec17.pdf