多维梯度下降

多维函数梯度（偏导数组成）

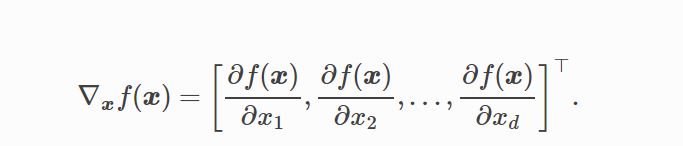
方向导数：

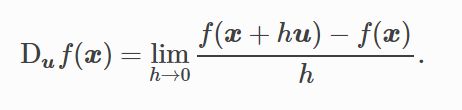
迭代方程：

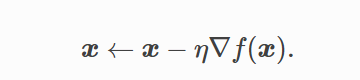
import math
import matplotlib
import numpy as np
import gluonbook as gb
from mxnet import nd,autograd,init,gluon

eta = 0.1
def f_2d(x1,x2):
    return x1**2 + 2*x2**2

def gd_2d(x1,x2,s1,s2):
    return (x1 - eta*2*x1,x2-eta*4*x2,0,0)

def train_2d(trainer):
    x1, x2, s1, s2 = -5, -2, 0, 0
    results = [(x1,x2)]
    for i in range(20):
        x1, x2, s1, s2 = trainer(x1,x2,s1,s2)
        results.append((x1,x2))
    return results

def show_trace_2d(f,results):
    gb.plt.plot(*zip(*results),'-o',color='#ff7f0e')
    x1,x2 = np.meshgrid(np.arange(-5.5,1.0,0.1),np.arange(-3.0,1.0,0.1))
    gb.plt.contour(x1,x2,f(x1,x2),colors='#1f77b4')
    gb.plt.xlabel('x1')
    gb.plt.ylabel('x2')

show_trace_2d(f_2d,train_2d(gd_2d))

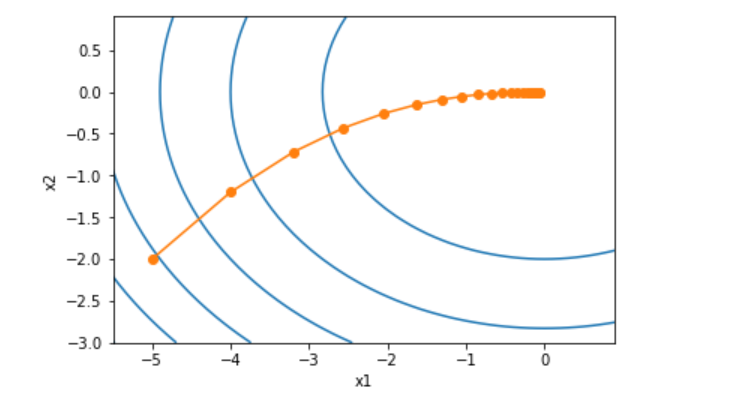
发现，最优值取值在x1=0,x2=0 附近