蓝桥杯《操作格子》

　　解题过程：题意通俗易懂，看完题目以为是普通的对数组进行操作的题目，但是看到输入的数据范围后，发现并不是。但是因为没有好的想法，只能用最简单的方式做，毫无意外的超时了。然后找到这篇博文：http://blog.csdn.net/qq_33245342/article/details/54892576

问题描述 

有n个格子，从左到右放成一排，编号为1-n。 
共有m次操作，有3种操作类型： 
1.修改一个格子的权值， 
2.求连续一段格子权值和， 
3.求连续一段格子的最大值。 
对于每个2、3操作输出你所求出的结果。 

输入格式 
第一行2个整数n，m。 
接下来一行n个整数表示n个格子的初始权值。 
接下来m行，每行3个整数p,x,y，p表示操作类型，p=1时表示修改格子x的权值为y，p=2时表示求区间[x,y]内格子权值和，p=3时表示求区间[x,y]内格子最大的权值。 

输出格式 
有若干行，行数等于p=2或3的操作总数。 
每行1个整数，对应了每个p=2或3操作的结果。 

样例输入 
4  3 
1  2  3  4 
2  1  3 
1  4  3 
3  1  4 

样例输出 
6 
3 

数据规模与约定 
对于20%的数据n  < =  100，m  < =  200。 
对于50%的数据n  < =  5000，m  < =  5000。 
对于100%的数据1  < =  n  < =  100000，m  < =  100000，0  < =  格子权值  < =  10000。

细节：

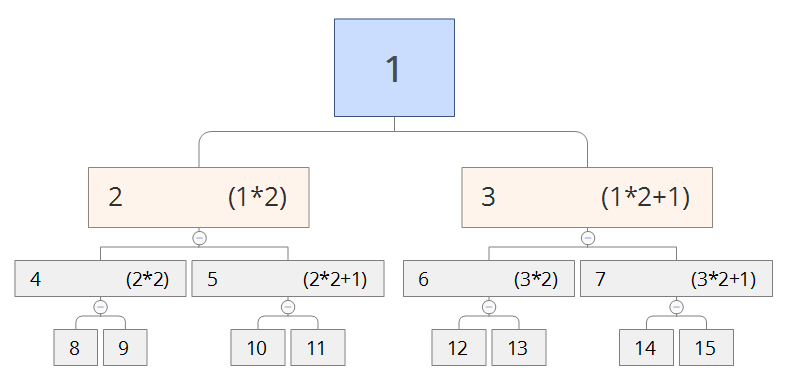
1. 关于树节点的顺序排号：某个节点的子节点序号=自身节点*2（+1右子节点才需要）

        

        

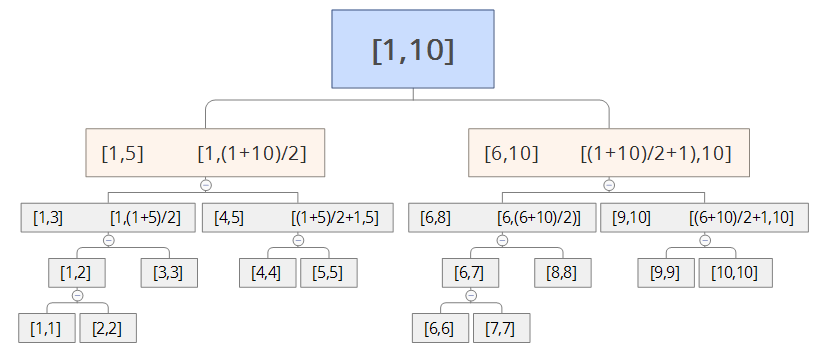
　　2. 关于区间的控制

　　每个几点都有两个int变量存储当前节点所存储的数据表示是与这一区间相关。

//  操作格子
#include<stdio.h>
#define Num 100000

// 创建树的结点
struct Node{
    // [left, right]    记录这个结点和这个结点的子节点（如果有）的取值范围
    // sum记录当前结点的取值范围的总和
    // max记录当前结点的最大值
    int left,right,sum,max;
}Tree[Num*3];

int length=0;

// 初始化树
// p    是当前的位置
// left 是当前结点要存储的左值
// right 是当前结点要存储的右值
void SetTree(int p, int left, int right){
    // 记录结点的个数
    length++;
    
    if(left==right){
        Tree[p].left=left;
        Tree[p].right=left;
        Tree[p].sum=left;
        Tree[p].max=left;
        return;
    }
    Tree[p].left=left;
    Tree[p].right=right;

    // 右边的子树    [left, right/2]
    int mid = (left+right)>>1;
    SetTree(p*2,left,(mid));
    // 左边的子树    [right/2+1, right];
    SetTree(p*2+1,mid+1,right);

    Tree[p].sum = Tree[p*2].sum+Tree[p*2+1].sum;
    Tree[p].max = Tree[p*2].max>Tree[p*2+1].max?Tree[p*2].max:Tree[p*2+1].max;
    
    return;
}

void Change(int p, int x, int y){
    if(Tree[p].left==Tree[p].right){
        // 不改变左右值，因为左右值用来做位置的标记
        // Tree[p].left=y;
        // Tree[p].right=y;
        Tree[p].sum=y;
        Tree[p].max=y;
        return;
    }
    int mid=Tree[p*2].right;
    if(mid>=x)  Change(p*2, x, y);
    else Change(p*2+1,x,y);

    Tree[p].sum = Tree[p*2].sum+Tree[p*2+1].sum;
    Tree[p].max = Tree[p*2].max>Tree[p*2+1].max?Tree[p*2].max:Tree[p*2+1].max;
    return;
}

int Find(int p, int x, int y, int choose){
    if(Tree[p].left==x && Tree[p].right==y){
        if(choose==2) return Tree[p].sum;
        else return Tree[p].max;
    }
    int mid=Tree[p*2].right;
    if(mid>=y)  return(Find(p*2, x, y, choose));
    else if(mid<x) return(Find(p*2+1, x, y, choose));

    // 考虑选择的区间刚好不是先有的结点，需要额外的处理
    int le = Find(p * 2, x, mid,choose);  
    int ri = Find(p * 2 + 1, mid + 1, y,choose);  

    if(choose==2)   return le+ri;
    else return (le>ri?le:ri);
}

int main(void){
    // nc   =   numcount
    // cc   =   changecount
    int nc,cc;
    int r1=1,num;
    
    scanf("%d%d",&nc,&cc);
    SetTree(1,1,nc);

    // [0,0]
    // 检查区间
    // for(;r1<=length;r1++) printf("[%2d,%2d]
",Tree[r1].left,Tree[r1].right);
    // return 0;

    // 1.修改一个格子的权值
    // 2.求连续一段格子权值和 
    // 3.求连续一段格子的最大值
    for(r1=1;r1<=nc;r1++){
        scanf("%d",&num);
        // 因为当前树已经按照自然数排序初始化了，如果当前输入的数字与序号相同，那么就不需要做处理
        if(r1==num) continue;
        Change(1,r1,num);
    }

    int a,b;
    for(r1=1;r1<=cc;r1++){
        scanf("%d%d%d",&num,&a,&b);
        switch(num){
            case 1: Change(1,a,b); break;
            case 2: printf("%d
",Find(1,a,b,2));  break;
            case 3: printf("%d
",Find(1,a,b,3));  break;
        }
    }

    return 0;
}