选择排序

算法思想

从左到右依次比较,找出全部无序最小的元素与数组中的第一个元素进行交换;然后从第数组中第二个元素
开始比较,找出剩余无序元素中最小的的元素,然后将其与数组中的第二个元素进行交换,按照这种方式操作
下去直到数组有序

例:升序排序8,1,6,3,2,4

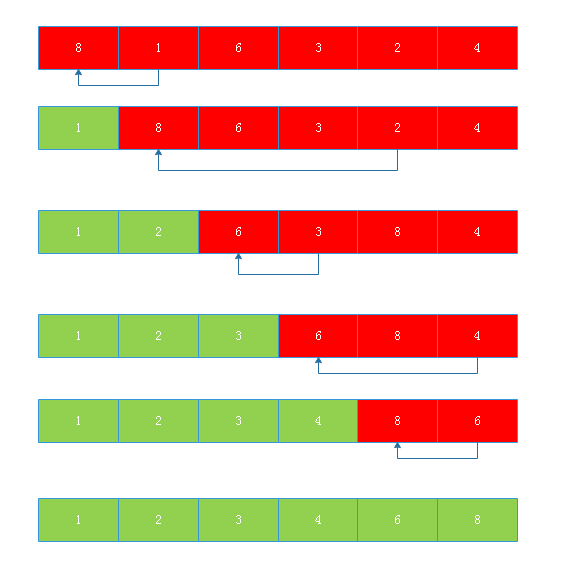
代码实现

bool SelectionSort(int *pAry, int nSize)
{
  if (pAry == nullptr || nSize <= 0)
  {
    return false;
  }

  for (int iIndex = 0; iIndex < nSize-1; iIndex++)
  {
    int nIndexOfMinValue = iIndex;
    for (int jIndex = iIndex+1; jIndex < nSize; jIndex++)
    {
      if (pAry[nIndexOfMinValue] > pAry[jIndex])
      {
        nIndexOfMinValue = jIndex;
      }
    }

    if (nIndexOfMinValue != iIndex)
    {
      int nTemp = pAry[nIndexOfMinValue];
      pAry[nIndexOfMinValue] = pAry[iIndex];
      pAry[iIndex] = nTemp;
    }
  }

  return true;
}

测试代码:

void PrintData(int*pAry, int nSize)
{
  for (int jIndex = 0; jIndex < nSize; jIndex++)
  {
    printf("%d ", pAry[jIndex]);
  }
  printf("
");
}

int main()
{
  srand(time(NULL));

  int nArry[20] = { 0 };

  for (int jIndex = 0; jIndex < 10; jIndex++)
  {
    for (int iIndex = 0; iIndex < sizeof(nArry) / sizeof(nArry[0]); iIndex++)
    {
      nArry[iIndex] = rand() % 150;
    }
    printf("排序前:");
    PrintData(nArry, sizeof(nArry) / sizeof(nArry[0]));
    SelectionSort(nArry, sizeof(nArry) / sizeof(nArry[0]));
    printf("排序后:");
    PrintData(nArry, sizeof(nArry) / sizeof(nArry[0]));
  }
  return 0;
}

测试结果:

时间复杂度分析

假设待排序元素有n个,核心部分代码如下:

//执行n次
 for (int iIndex = 0; iIndex < nSize-1; iIndex++)
{
    //执行n-1次
    int nIndexOfMinValue = iIndex;
    //执行1+2+...+n次
    for (int jIndex = iIndex+1; jIndex < nSize; jIndex++)
    {
      //执行1+2+...+n-1次
      if (pAry[nIndexOfMinValue] > pAry[jIndex])
      {
        //最好的情况下:执行0次
        //最好的情况下:执行1+2+...+n-1次
        nIndexOfMinValue = jIndex;
      }
    }
   
    //执行n-1次
    if (nIndexOfMinValue != iIndex)
    {
      //最好的情况下:执行0次
      //最好的情况下:n-1次
      int nTemp = pAry[nIndexOfMinValue];
      pAry[nIndexOfMinValue] = pAry[iIndex];
      pAry[iIndex] = nTemp;
    }
}

最好的情况下(排序前数组中的元素已经有序了):
T(n) = n+(n-1)+(1+2+...+n)+(1+2+.....+n-1)+(n-1) = n^2+3n-2 = O(n^2)
最坏的情况下(排序前数组中的元素是逆序的):
T(n) =n+(n-1)+(1+2+...+n)+2*(1+2+.....+n-1)+2*(n-1)=(5/2)*n+(3/2)*(n^2)-3=O(n^2)

稳定性

例如:5,2,6,4,2,1
第一轮排序后为:5,2,1,4,2,6
第二轮排序后为:2,2,1,4,5,6
此时两个相同元素2的位置已经发生颠倒,所以选择排序是不稳定的