20162317-20162315结对编程（四则运算）第二周阶段总结

20162317-20162315结对编程（四则运算）第二周阶段总结

• 四则运算

需求分析

• 实现真分数的四则运算。四则运算的框架任然可以使用原来的栈对后缀表达式进行计算。难度的增加体在真分数的构建以及真分数的四则运算。

设计思路

• 在上一次的基础上，要弄出一段代码是创建一个分数的方法。因此我在构造函数中添加了参数以此来设计分数的分子和分母。

public Fraction(int top,int bottom){

            this.top = top;
            this.bottom = bottom;
    }
    public int getTop(){
        return  top;
    }
    public int getBottom(){return  bottom;}

    但是分数并不是用户自己建立的而是随机出现的，因而在该类的setQuestions里面我用这个类在方法里建立分数对象，然后再用随机Random来随机设计一个分数，并且保证是真分数。

 public void setQuestion(int chseNum,int chseDif){
        Fraction f1 ;
        middle = new String[2 * (chseDif + 1)];
        for(int t=1;t<=chseNum;t++){
            for(int i =0 ; i<middle.length;i+=2){
                while (true) {
                    int intop = r.nextInt(10) + 1;
                    int inbottom = r.nextInt(10) + 1;
                    if(intop < inbottom){
                        f1 = new Fraction(intop,inbottom);
                        break;
                    }
                }

                String fr1 = String.valueOf(f1.getTop())+"/"+String.valueOf(f1.getBottom());
                middle[i] = String.valueOf(fr1);
            }

    此外，还有一点头疼的就是分数的晕死算，分数并不像整数或小数那样能够直接进行运算，分数的运算还要复杂，除的话你要考虑倒数，加减的话你要考虑通分。因此，原来的运算方式也不能要了，对应的，要改为分数的运算方式。在课本中有一段代码就是关于有理数的运算，我稍作修改，将其用到我的程序中。

    public Fraction add (Fraction op1 ,Fraction op2)
    {
        result = new Fraction(1,1);
        int commonDenominator = op1.getBottom() * op2.getBottom();
        int top1 = op1.getTop() * op2.getBottom();
        int top2 = op2.getTop() * op1.getBottom();
        int sum = top1 + top2;
        result = new Fraction (sum, commonDenominator);
        return result;
    }
    //-----------------------------------------------------------------
// Subtracts the rational number passed as a parameter from this
// rational number.
//-----------------------------------------------------------------
    public Fraction subtract (Fraction op1,Fraction op2)
    {
        result = new Fraction(1,1);
        int commonDenominator = op1.getBottom() * op2.getBottom();
        int top1 = op1.getTop() * op2.getBottom();
        int top2 = op2.getTop() * op1.getBottom();
        int difference = top1 - top2;
        result=new Fraction (difference, commonDenominator);
        return result;
    }
    //-----------------------------------------------------------------
// Multiplies this rational number by the one passed as a
// parameter.
//-----------------------------------------------------------------
    public Fraction multiply (Fraction op1,Fraction op2)
    {

        result = new Fraction(1,1);
        int numer = op1.getTop() * op2.getTop();
        int denom = op1.getBottom() * op2.getBottom();
        result= new Fraction (numer, denom);
        return  result;
    }
    //-----------------------------------------------------------------
// Divides this rational number by the one passed as a parameter
// by multiplying by the reciprocal of the second rational.
//-----------------------------------------------------------------
    public Fraction divide (Fraction op1, Fraction op2)
    {
        return multiply (op1,op2.DaoShu());
    }

解决了分数的建立以及分数的运算，剩下的就是如何判断的问题了，计算后不能光光根据它们的小数是否相等，这样做的做法不科学，不严谨。因此我将其最后反馈答案都用fraction类表现出来，如此一来，结果和用户结果都是分数类了，从而比较就用双方的分子是否相等，以及双方的分母是否相等的方法来判断

  public boolean isLike(Fraction fraUsrAns,Fraction result){
        return (fraUsrAns.getTop()== result.getTop() &&
                fraUsrAns.getBottom()==result.getBottom());
    }

若用这种方法来判断的话还要设立一个标准，所以要求分数要做到最简分数，就要用到约分，根据约分的原理我用这样一段代码来实现约分。

private void YueFen(Fraction result)
    {
        if (result.top != 0)
        {
            int common = gcd (Math.abs(result.top), result.bottom);
            result.top = result.top / common;
            result.bottom = result.bottom / common;
        }
    }
     private int gcd (int num1, int num2)
    {
        while (num1 != num2)
            if (num1 > num2)
                num1 = num1 - num2;
            else
                num2 = num2 - num1;
        return num1;
    }

• 如何将得到的结果约分？
• 最开始我们不知道怎么去约分，输出的时候结果都是没有约分过的分数，后来我查到了Math里面取出公约数的方法，将分子分母同时除以公约数输出的时候得到的便是其最简形式了。
  最后我写了一个setQuestions的主函数，用来将整数的计算还有分数的计算进行联系。代码如下

/**
 * Created by Funny_One on 2017/5/23.
 */
import java.util.Scanner;
import java.util.Random;
public class SetQuestions {
    public static void main(String[] args)throws Exception {
        int chseNum = 0, chseDif = 0;
        Scanner sca = new Scanner(System.in);
        Random r = new Random();
        final int INTEGER = 1;
        //Design the number of questions that the customers want to try.


        System.out.println("How many questions do you want to try?");
        chseNum = sca.nextInt();


        System.out.println("What level do you want to challenge ?(from 1 to 5)");
        chseDif = sca.nextInt();

        int choose = r.nextInt(2);
        if (choose == INTEGER) {
            iInteger i = new iInteger();
            i.offerQuestion(chseNum, chseDif);
        }else{
            Fraction f =new Fraction();
            f.setQuestion(chseNum,chseDif);

        }
    }
}

遭遇问题

• 测试的时候有时候明明是对的，输出却是You are wrong.
• 最开始设置的是识别三个字符串长度的运算结果。所以分子分母只要超过一位就会错误，重新修改后已解决。

原代码

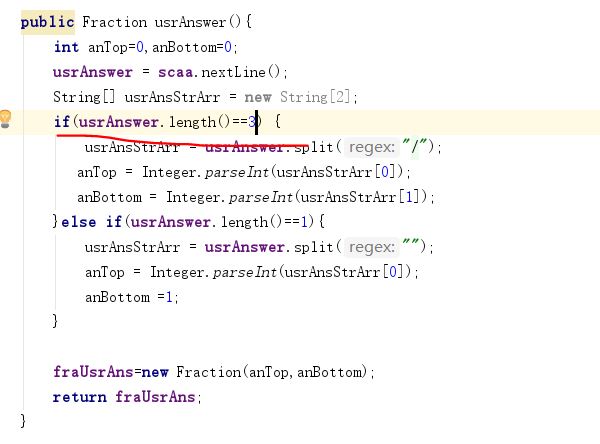
当时的目的是为了能够使程序识别用户答案是分数还是整数，整数那段代码还好说，但是分数那段代码就不科学了，这样的限制导致分子分母只能为一位数。因此，我将其改成了这样：

现代码

UML类图

---

Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
计划	（第一周）20/（第二周）30	（第一周）40/（第二周）80
·估计耗时	（第一周）20/（第二周）25	（第一周）40/（第二周）/65
开发	（第一周）435/（第二周）500	（第一周）525/（第二周）600
·需求分析	（第一周）30/(第二周）15	（第一周）50/（第二周）8
·生成设计文档	（第一周）20/（第二周）25	（第一周）30/（第二周）20
·具体设计	（第一周）30/(第二周）50	（第一周）50 /（第二周）80
·具体编码	（第一周）300/（第一周）450	（第一周）320/（第二周）600
·代码复审	（第一周）30/(第一周）120	（第一周）15/（第二周）80
·测试	（第一周）25/（第二周）15	（第一周）60/（第二周）30
报告	（第一周）105/(第二周）90	（第一周）110/（第二周）160
·测试报告	（第一周）50/（第二周）65	（第一周）80/（第二周）80
·事后总结，并提出过程改进计划	（第一周）35（第二周）65	（第一周）20/（第二周）32
·分析下一步计划	（第一周）20/（第二周）20	(第一周）10/（第二周）40
合计	（第一周）460/（第二周）1470	（第一周）675（第二周）1885

结队伙伴：
马军20162315