学号 2017-2018-1 《程序设计与数据结构》第1周学习总结
教材学习内容总结
1、算法与效率的关系
对于同一算法
输入量小,速度快;
输入量大,速度慢。
对于不同的算法
有可能在n的某一区间,一个算法的速度高于另一个;
而在n的另一区间,情况可能就会相反。
对于不同的算法
规模较小时,算法效率接近;
规模扩大,算法效率通常呈上升趋势,各算法之间的差距就比较明显了。
2、增长函数的作用:显示了与问题大小相关的时间或空间利用率;
3、渐近复杂度:当问题规模n增大时函数的一般特性;
4、主项:对于一个函数,问题规模n增大时变化最快的一项。
5、程序 = 算法 + 数据内容
6、数据结构的专业术语:数据,数据元素,数据项,数据结构
7、算法:在特定计算模型下,旨在解决特定问题的指令序列(蛮力法,分治法,贪婪法,回溯法);
8、算法的特点:输入、输出、正确性、确定性、可行性、有穷性;
9、图灵机中的元素:Tape(带),Alphabet(字母表),Head(读写头),State(状态),Transition Function。
10、大O记号,大Ω记号,大Θ记号:

11、幂方级数:比幂次高一级,收敛级数:O(1),调和级数,对数级数
12、冒泡排序:有序/无序序列中,任意/总有一对相邻的元素顺序/逆序。依次比较每一对相邻元素,如有必要,交换之,否则,再做一趟扫描交换。
特点:不变性、单调性、正确性。
13、空间复杂度:除了输入所占的空间之外,其他计算必需的空间总量。
14、分而治之:为求解某一个大规模的问题,可以将其划分为若干(通常两个)子问题,规模大体相当,分别求解子问题,由子问题的解,得到原问题的解。
15、语句频度
教材学习中的问题和解决过程
问题一:这一章设计到上一章的递归,由于上学期对递归只是浅显的了解,所以并不清楚递归的实际操作。
问题1解决方案:为了解决问题,我正式自学了11章的递归,虽在11章的代码遇到了问题,但通过debug解决了问题。至此,现在对递归的了解就加深了。
问题2:for(int i = 1; i < n ; i++ )的语句频度为何是(n+1),不是就循环了n次吗?
问题2的解答:以上的循环可以等同于:
i=1---------------O(1)
while(i<n){--------------O(n)
i++;
}
因此是n+1;
代码调试中的问题和解决过程
- 问题1:代码的问题主要都出在一个递归中。
- 问题1解决方案:程序设计与数据结构有关递归的学习:迷宫项目](http://note.youdao.com/)
代码托管

上周考试错题总结
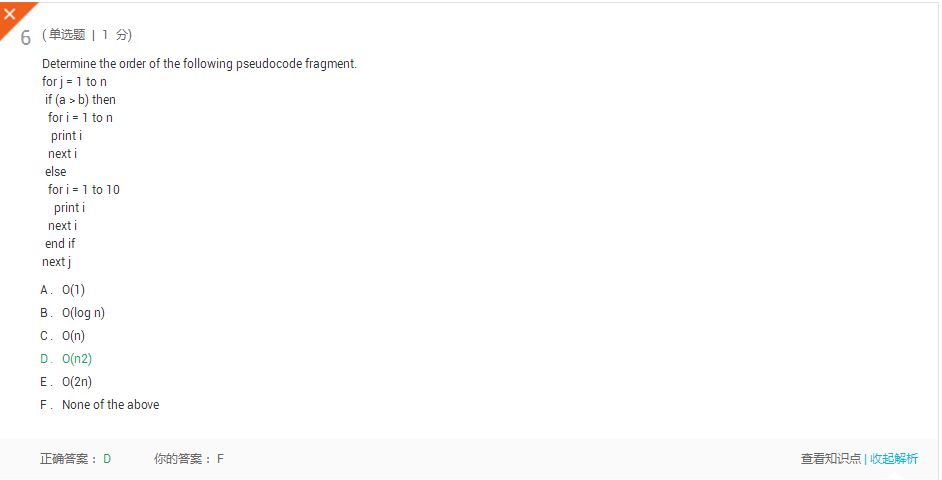
这个代码片段的最坏情况时间复杂度是O(n2)。在最好的情况下,它是O(n)。如果不进一步了解A和B,就不可能找到平均情况下的时间复杂度,除非另有说明,算法的顺序是指其最坏情况时间复杂度。
结对及互评
点评模板:
-
博客中值得学习的或问题:
- 排版精美
- 内容准确
-
其他
- 马军同学思考的得比较细心,问题不流露于表面,说明学习和上课都比较细心。
本周结对学习情况
[20162315](http://www.cnblogs.com/cs162315/p/7502024.html)
结对学习内容
马军同学提到的上面教材问题中的算法的复杂度到底是O(n)还是O(1)的问题。
书上P296的算法复杂度的判断。
其他(感悟、思考等,可选)
算法已经超越解决问题的层次了,而是要更好地解决问题,这无疑也对我们的打码任务给了更大的挑战。这意味着更好,更短,更有效率的代码。这是一个坎。不过,跨过这道坎之后我们的打代码技术会产生质变。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 20篇 | 400小时 | |
| 第一周 | 614/614 | 2/2 | 12/12 |
-
计划学习时间:10小时
-
实际学习时间:12小时
-
改进情况:
不像上个学期那样比较应付,遇到不会的会以更加积极的态度来解决。