2SAT

最小字典序的2-SAT

（以下文字嫖自网上）

【O(NM)算法：求字典序最小的解】
根据2-SAT建成的图中边的定义可以发现，若图中i到j有路径，则若i选，则j也要选；或者说，若j不选，则i也不能选；
因此得到一个很直观的算法：
（1）给每个点设置一个状态V，V=0表示未确定，V=1表示确定选取，V=2表示确定不选取。称一个点是已确定的当且仅当其V值非0。设立两个队列Q1和Q2，分别存放本次尝试选取的点的编号和尝试不选的点的编号。
（2）若图中所有的点均已确定，则找到一组解，结束，否则，将Q1、Q2清空，并任选一个未确定的点i，将i加入队列Q1，将i'加入队列Q2；
（3）找到i的所有后继。对于后继j，若j未确定，则将j加入队列Q1；若j'（这里的j'是指与j在同一对的另一个点）未确定，则将j'加入队列Q2；
（4）遍历Q2中的每个点，找到该点的所有前趋（这里需要先建一个补图），若该前趋未确定，则将其加入队列Q2；
（5）在（3）（4）步操作中，出现以下情况之一，则本次尝试失败，否则本次尝试成功：
　　<1>某个已被加入队列Q1的点被加入队列Q2；
　　<2>某个已被加入队列Q2的点被加入队列Q1;
　　<3>某个j的状态为2；
　　<4>某个i'或j'的状态为1或某个i'或j'的前趋的状态为1；
（6）若本次尝试成功，则将Q1中的所有点的状态改为1，将Q2中所有点的状态改为2，转（2），否则尝试点i'，若仍失败则问题无解。
该算法的时间复杂度为O(NM)（最坏情况下要尝试所有的点，每次尝试要遍历所有的边），但是在多数情况下，远远达不到这个上界。
具体实现时，可以用一个数组vst来表示队列Q1和Q2。设立两个标志变量i1和i2（要求对于不同的i，i1和i2均不同，这样可以避免每次尝试都要初始化一次，节省时间），

若vst[i]=i1则表示i已被加入Q1，若vst[i]=i2则表示i已被加入Q2。不过Q1和Q2仍然是要设立的，因为遍历（BFS）的时候需要队列，为了防止重复遍历，加入Q1（或Q2）中的点的vst值必然不等于i1（或i2）。

中间一旦发生矛盾，立即中止尝试，宣告失败。

该算法虽然在多数情况下时间复杂度到不了O(NM)，但是综合性能仍然不如下面的O(M)算法。不过，该算法有一个很重要的用处：求字典序最小的解！
如果原图中的同一对点编号都是连续的（01、23、45……）则可以依次尝试第0对、第1对……点，每对点中先尝试编号小的，若失败再尝试编号大的。

这样一定能求出字典序最小的解（如果有解的话），因为一个点一旦被确定，则不可更改。
如果原图中的同一对点编号不连续（比如03、25、14……）则按照该对点中编号小的点的编号递增顺序将每对点排序，然后依次扫描排序后的每对点，

先尝试其编号小的点，若成功则将这个点选上，否则尝试编号大的点，若成功则选上，否则（都失败）无解。

具体注释都在板子里了。

Peaceful Commission 裸的2-SAT

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20010;
struct E{int to, nex;} edge[N*10];
int cnt, head[N];
int n, m, top;
int sta[N];
bool mark[N];
void add_edge(int v, int u) {
    edge[cnt] = {u, head[v]};
    head[v] = cnt++;
}
//算法复杂度为O(nm) 大多情况是跑不到的

bool dfs(int v) {
     //在同一个集合里的两个元素都被染成1了，出现冲突
    if (mark[v^1]) return 0;
    //要染的点已经染成要染的颜色了。直接返回
    if (mark[v]) return 1;
    sta[top++] = v; //记录染色的点
    mark[v] = 1;    //将v的颜色染成1
    for(int i = head[v]; ~i; i = edge[i].nex) {
        int u = edge[i].to;
        if (!dfs(u)) return 0; //出现冲突直接返回
    }
    return 1; //未出现冲突
}

bool solve() {
    memset(mark, 0, sizeof mark);
    //已经按字典序从小到大染色了
    for(int i = 0; i < 2*n; i += 2) {
     //这个集合中两个点都没被染色。那么强制将第一个点染成1
        if(!mark[i] && !mark[i+1]) {
            top = 0;
            //将第一个点染色出现了冲突。那么还原，并将第二个点染色成1
            if(! dfs(i)) {
                for(int i = 0; i < top; i++) mark[sta[i]] = 0; //还原
                if (!dfs(i+1)) return 0; //如果第二个点都不能染成1，那么问题无解直接返回
            }
        }
    }
    return 1;
}

void init() {
    cnt = 0;
    memset(head, -1, sizeof head);
}

int main() {
    while (~scanf("%d%d", &n, &m)) {
        init();
        for(int i = 1,u,v; i <= m; i++) {
            scanf("%d%d", &v, &u), v--, u--; //方便异或建边，所以最小编号要从0开始
            add_edge(v, u^1), add_edge(u, v^1); //冲突建边
        }
        if (solve()) {
            for(int i = 0; i < 2*n; i += 2)
                //一个集合中只能选一个元素。
                if (mark[i]) printf("%d\n", i+1);
                else printf("%d\n", i+2);
        }
        else printf("NIE\n");
    }
    return 0;
}

一般的2-SAT

【O(M)算法】
根据图的对称性，可以将图中所有的强连通分支全部缩成一个点（因为强连通分支中的点要么都选，要么都不选），

然后按照拓扑逆序（每次找出度为0的点，具体实现时，在建分支邻接图时将所有边取反）遍历分支邻接图，将这个点（表示的连通分支）选上，

并将其所有对立点（注意，连通分支的对立连通分支可能有多个，若对于两个连通分支S1和S2，点i在S1中，点i'在S2中，则S1和S2对立）及这些对立点的前趋全部标记为不选，直到所有点均标记为止。

这一过程中必然不会出现矛盾（详细证明过程省略，论文里有）。
无解判定：若求出所有强分支后，存在点i和i'处于同一个分支，则无解，否则必定有解。
时间复杂度：求强分支时间复杂度为O(M)，拓扑排序的时间复杂度O(M)，总时间复杂度为O(M)。
该算法的时间复杂度低，但是只能求出任意一组解，不能保证求出解的字典序最小。当然，如果原题不需要求出具体的解，只需要判定是否有解（有的题是二分 + 2-SAT判有解的），

当然应该采用这种算法，只要求强连通分支（Kosaraju、Tarjan均可，推荐后者）即可。

Priest John's Busiest Day

题意（源自

有一个小镇上只有一个牧师。这个小镇上有一个传说，在九月一日结婚的人会受到爱神的保佑，但是要牧师举办一个仪式。这个仪式要么在婚礼刚刚开始的时候举行，要么举行完婚礼正好结束。
现在已知有n场婚礼，告诉你每一场的开始和结束时间，以及举行仪式所需要的时间。问牧师能否参加所有的婚礼，如果能则输出一种方案。

可能上面的题意还没讲清楚，先上一张图。



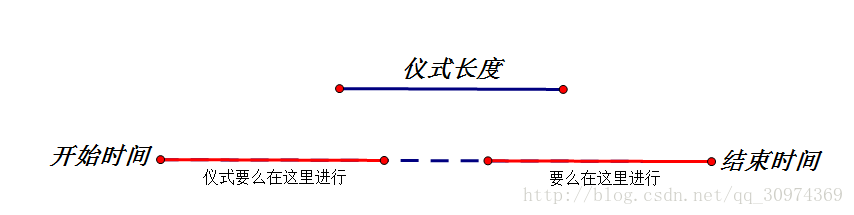
现在应该就非常清楚了。
继续化简题目：有n*2条线段，其中每两条（我设的是i和i+n）中只能够选择一条，问能否给出n条线段使得任意两条不存在交点。
一组（或者一个）东西有且仅有两种选择，要么选这个，要么选那个，还有一堆的约束条件。
这是一个很明显的2-sat问题。

看到没，还是两个时间点交叉出现的时候存在重合
只需要加判断是否重合然后建边了。

接下来的一步和POJ 3207 也是一样的，Tarjan缩点，判断是否可行

但是，这题多一个步骤，要求出一组可行性解。
根据Dalao的Blog(在上面的第一个链接里面有dalao博客的链接)，这一步应该进行拓扑排序,然后依次尝试染色（此时必定有解）即可。

这题就讲这么多，其他的具体实现参考一下代码。

存个板子

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn = 10000 + 500;
int color[maxn], In[maxn], len[maxn], Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int n;
vector<int> G[maxn];//超级点就用vector来存边,方便些

struct Time{
    int bg, ed;
} t[maxn];

struct Node{
    int v, nex;
}edge[maxn*maxn];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

bool check(int i,int j){ return !(t[i].bg>=t[j].ed||t[i].ed<=t[j].bg);}

void Build() {
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            if (i == j) continue;
            if (check(i, j)) Add(i, j+n); //开头和开头矛盾
            if (check(i, j+n)) Add(i, j); //开头和结尾矛盾
            if (check(i+n, j)) Add(i+n, j+n); //结尾和开头矛盾
            if (check(i+n, j+n)) Add(i+n, j); //结尾和结尾矛盾
        }
    }
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}
void Build_New() {
    for (int i = 1; i <= 2*n; ++i) {
        for(int j = head[i]; ~j; j = edge[j].nex){
            int v = edge[j].v;
            if (belong[i] == belong[v]) continue;
            G[belong[v]].push_back(belong[i]);//边要反着存
            In[belong[i]] ++;//统计入度
        }
    }
}
void topu() {
    memset(In, 0, sizeof(In));
    memset(color, -1, sizeof(color));
    //缩点之后建新图
    Build_New();
    queue<int> q;//拓扑排序的队列
    for (int i = 1; i <= sccNum; ++i)
        if (!In[i]) q.push(i); //入度为0的进队
    while (!q.empty()) {
        int v=q.front();
        q.pop();
        if(color[v] == -1) { // -1为未染色
            color[v] = 1;     //染为1
            color[Opp[v]] = 0; //对立点染为0
        }
        for (int i = 0; i < G[v].size(); ++i)  //依次减入度
            if (--In[G[v][i]] == 0) q.push(G[v][i]); //入度为0
    }
}
void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(In, 0, sizeof(In));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

int main() {
    while (~scanf("%d", &n)) {
        init();
        for (int i = 1; i <= n; ++i) {
            int a, bg, c, d, ed;
            scanf("%d:%d %d:%d %d",
                  &a, &bg, &c, &d, &len[i]);
            t[i].bg = a * 60 + bg;
            t[i+n].ed = c * 60 + d;
            t[i].ed = t[i].bg + len[i];
            t[i+n].bg = t[i+n].ed - len[i];
        }
        Build();
        for (int i = 1; i <= 2*n; ++i)//缩点
            if (!dfn[i]) Tarjan(i);

        for (int i = 1; i <= n; ++i) {//判断是否有解
            if (belong[i] == belong[i+n]) {//某个婚礼的 开始/结束 在同一个强连通分量中，无解
                cout << "NO" << endl;
                return 0;
            }
            Opp[belong[i]] = belong[i+n]; //存一下超级点的的对立点
            Opp[belong[i+n]] = belong[i]; //反向也要存
        }

        cout << "YES" << endl;//不存在矛盾，则有解
        topu();//Top排序
        for (int i = 1; i <= n; ++i) {
            if (color[belong[i]] == 1) //选择了再婚礼开始时
                printf("%.2d:%.2d %.2d:%.2d\n",t[i].bg/60,t[i].bg%60,t[i].ed/60,t[i].ed%60);
            else //在婚礼结束时
                printf("%.2d:%.2d %.2d:%.2d\n",t[i+n].bg/60,t[i+n].bg%60,t[i+n].ed/60,t[i+n].ed%60);
        }
    }
}

还有一般的建图策略：

模型一：两者（A，B）不能同时取

　　那么选择了A就只能选择B’，选择了B就只能选择A’
　　连边A→B’，B→A’

模型二：两者（A，B）不能同时不取

　　那么选择了A’就只能选择B，选择了B’就只能选择A
　　连边A’→B，B’→A

模型三：两者（A，B）要么都取，要么都不取

　　那么选择了A，就只能选择B，选择了B就只能选择A，选择了A’就只能选择B’，选择了B’就只能选择A’
　　连边A→B，B→A，A’→B’，B’→A’

模型四：两者（A，A’）必取A

　　那么，那么，该怎么说呢？先说连边吧。
　　连边A’→A

Party

题面是中文就不多说。前面的题目大多都是存个板子。这才是自己第一道写的2-SAT。

先说说感想。这道题一开始我就看出是很裸的2-SAT。但是却WA了。

看到HDU的讨论区有人问了这样的问题。

Re:为什么每个关系建两条边而不是四条

如题：
只建两条边：
sat.add_edge(b,a^1);
sat.add_edge(a,b^1);
就可以AC，
而建四条边：
sat.add_edge(a^1,b);
sat.add_edge(b,a^1);
sat.add_edge(a,b^1);
sat.add_edge(b^1,a);
会WA，有人知道怎么回事吗？
----------------------------------------------------------------------------------
选a后只能选b^1
选a^1后没有限制,再选b或b^1都行
b同理
看了红字以后我才明白我之前的建图有什么错误。
之前我是这么建图的

if (c1 && c2 || !c1 && !c2) Add(a1, a2+n), Add(a1+n, a2);  //夫夫，妇妇有矛盾
else Add(a1, a2), Add(a1+n, a2+n); //夫妇，妇夫有矛盾

但是很明显这是错的。这就是我没明白2-SAT建图的意义。不过现在倒是明白了。以下是AC代码。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn = 1e6 + 500;
int color[maxn], In[maxn], len[maxn], Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int n, m;

struct Node{
    int v, nex;
}edge[maxn];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(In, 0, sizeof(In));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

int main() {
    while (~scanf("%d", &n)) {
        init();
        scanf("%d", &m);
        for (int i = 1; i <= m; ++i) {
            int a1, a2, c1, c2;
            scanf("%d%d%d%d", &a1, &a2, &c1, &c2);
            a1++, a2++;
            if(c1==0&&c2==0) {
                Add(a1+n, a2);
                Add(a2+n, a1);
            }
            else if(c1==0&&c2==1) {
                Add(a1+n,a2+n);
                Add(a2,a1);
            }
            else if(c1==1&&c2==0) {
                Add(a1,a2);
                Add(a2+n,a1+n);
            }
            else if(c1==1&&c2==1) {
                Add(a1,a2+n);
                Add(a2,a1+n);
            }
        }

        for (int i = 1; i <= 2*n; ++i)//缩点
            if (!dfn[i]) Tarjan(i);
        int flag = 0;
        for (int i = 1; i <= n && !flag; ++i) {//判断是否有解
            if (belong[i] == belong[i+n]) {//某个婚礼的 开始/结束 在同一个强连通分量中，无解
                flag = 1;
            }
            Opp[belong[i]] = belong[i+n]; //存一下超级点的的对立点
            Opp[belong[i+n]] = belong[i]; //反向也要存
        }
        if (flag) cout << "NO" << endl;
        else cout << "YES" << endl;//不存在矛盾，则有解

    }
}

Let's go home

这道题也是中文题面。但是他的题意也太不清晰了。就导致我一开始建边建错了。

现在发现2-SAT对与建边方向与状态真的有非常严格的要求。一定一定要理解题意。

给出题意：

    对于每一队：
    a, b, c （a是队长）
    若a不留下，b,c一定留下，若b,c中有一个人不留下，那么a一定留下。

    对于每一对：
    a, b
    若a 留下， b一定不留下
    若b 留下， a一定不留下
    注意的是a, b可以都不留下

AC代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn = 1e5 + 500;
int color[maxn], In[maxn], len[maxn], Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int t, m, n;

struct Node{
    int v, nex;
}edge[maxn];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(In, 0, sizeof(In));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

int main() {
    /*
    对于每一队：
    a, b, c （a是队长）
    若a不留下，b,c一定留下，若b,c中有一个人不留下，那么a一定留下。

    对于每一对：
    a, b
    若a 留下， b一定不留下
    若b 留下， a一定不留下
    注意的是a, b可以都不留下
    */
    while (~scanf("%d %d", &t, &m)) {
        init();
        n = 3*t;
        //0代表留下， n代表回家
        for (int i = 1; i <= t; ++ i) {
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            a++, b++, c++;
            Add(a+n, b), Add(a+n, c);
            Add(b+n, a), Add(c+n, a);
        }

        for (int i = 1; i <= m; ++i) {
            int a, b; scanf("%d%d", &a, &b);
            a++, b++;
            Add(a, b+n), Add(b, a+n); //因为ab其实可以一起回家。所以要这么写。
        }

        for (int i = 1; i <= 2*n; ++i)//缩点
            if (!dfn[i]) Tarjan(i);
        int flag = 0;
        for (int i = 1; i <= n && !flag; ++i) {//判断是否有解
            if (belong[i] == belong[i+n]) {//某个婚礼的 开始/结束 在同一个强连通分量中，无解
                flag = 1;
            }
            Opp[belong[i]] = belong[i+n]; //存一下超级点的的对立点
            Opp[belong[i+n]] = belong[i]; //反向也要存
        }
        if (flag) cout << "no" << endl;
        else cout << "yes" << endl;//不存在矛盾，则有解

    }
}

Bomb Game

算是对2-SAT有一个小小的理解了吧。起码这道题1A了。

题意：1.一对圆中必须选一个   2.求最小半径的最大值

题解：求最小值最大，用二分查找 ，冲突连边后用2-SAT判定

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
#define eps 1e-6
using namespace std;
const int maxn = 1e5 + 500;
int color[maxn], In[maxn], len[maxn], Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int t, m, n;

struct Node{
    int v, nex;
}edge[maxn];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(In, 0, sizeof(In));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

int a[maxn], b[maxn];

int dis(int i, int j){ return (a[i]-a[j])*(a[i]-a[j]) + (b[i]-b[j])*(b[i]-b[j]);}

bool check(double mid) {
    init();
    double r = mid;
    for (int i = 1; i <= n; i ++) {
        for(int j = i+1; j <= n; j ++) {
            if (r*r*4 >= dis(i, j)) Add(i, j+n), Add(j, i+n);
            if (r*r*4 >= dis(i+n, j)) Add(i+n, j+n), Add(j, i);
            if (r*r*4 >= dis(i, j+n)) Add(i, j), Add(j+n, i+n);
            if (r*r*4 >= dis(i+n, j+n)) Add(i+n, j), Add(j+n, i);
        }
    }
    for (int i = 1; i <= 2*n; ++i)//缩点
        if (!dfn[i]) Tarjan(i);
    for (int i = 1; i <= n; ++i) {//判断是否有解
        if (belong[i] == belong[i+n]) {//某个婚礼的 开始/结束 在同一个强连通分量中，无解
            return 0;
        }
        Opp[belong[i]] = belong[i+n]; //存一下超级点的的对立点
        Opp[belong[i+n]] = belong[i]; //反向也要存
    }
    return 1;
}

int main() {
    while (~scanf("%d", &n)) {
        for (int i = 1; i <= n; ++ i) {
            scanf("%d%d", &a[i], &b[i]);
            scanf("%d%d", &a[i+n], &b[i+n]);
        }
        double L=0, R=150000, ans=0;
        while (R - L > eps) {
            double mid = (L + R) / 2;
            if (check(mid)) L = mid;
            else R = mid;
        }
        printf("%.2f\n", L);
    }
}

Go Deeper

这道题我不是特别能理解。题意我倒是明白了。但是我不是很明白用2-SAT求的是什么。

先说说题意吧。

题意：给你一个递推式，问你最多能循环几层？

go(int dep, int n, int m) 
begin 
output the value of dep. 
if dep < m and x[a[dep]] + x[b[dep]] != c[dep] then go(dep + 1, n, m) 
end

问你最多能循环几层肯定就是想到用二分+2-SATcheck。

首先观察题目。C的取值[0, 2] , X的取值[0, 1]

那么我们可以把a[i]和b[i]当作一个点。x[ a[i] ]就是从这个点的取值。

那么这个点的取值有0有1所以就满足2-SAT的性质。

那我们继续分析：

若想循环下去，就要使第四行式子中“ x[a[dep]] + x[b[dep]] != c[dep]”成立，满足下面条件：

当c[i] == 0，有a[i] + n -> b[i] && b[i] + n -> a[i];

当c[i] == 1，有a[i] + n -> b[i] + n && b[i] + n -> a[i] + n && a[i] -> b[i] && b[i] -> a[i];

当c[i] == 2，有a[i] -> b[i] + n && b[i] -> a[i] + n;

连完边后跑2-SAT，答案问最大的，所以二分去求即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
#define eps 1e-6
using namespace std;
const int maxn = 1e5 + 500;
int color[maxn], In[maxn], len[maxn], Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int t, m, n;

struct Node{
    int v, nex;
}edge[maxn];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(In, 0, sizeof(In));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

int a[maxn], b[maxn], c[maxn];

int dis(int i, int j){ return (a[i]-a[j])*(a[i]-a[j]) + (b[i]-b[j])*(b[i]-b[j]);}

bool check(int mid) {
    init();
    for (int i = 1; i <= mid; i ++) {
        if(c[i] == 0) Add(a[i]+n, b[i]), Add(b[i]+n, a[i]);
        else if (c[i] == 1) {
            Add(a[i], b[i]), Add(b[i], a[i]);
            Add(a[i]+n, b[i]+n), Add(b[i]+n, a[i]+n);
        }
        else if (c[i] == 2) Add(a[i], b[i]+n), Add(b[i], a[i]+n);
    }
    for (int i = 1; i <= 2*n; ++i)//缩点
        if (!dfn[i]) Tarjan(i);
    for (int i = 1; i <= n; ++i) {//判断是否有解
        if (belong[i] == belong[i+n]) {//某个婚礼的 开始/结束 在同一个强连通分量中，无解
            return 0;
        }
        Opp[belong[i]] = belong[i+n]; //存一下超级点的的对立点
        Opp[belong[i+n]] = belong[i]; //反向也要存
    }
    return 1;
}

int main() {
    int T; scanf("%d", &T);
    while (T--) {
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= m; ++ i) {
            scanf("%d%d%d", &a[i], &b[i], &c[i]);
            a[i]++, b[i]++;
        }
        int L=0, R=m, ans=0;
        while (L <= R) {
            int mid = (L + R) / 2;
            if (check(mid)) {
                L = mid + 1;
                ans = max(ans, mid);
            } else R = mid - 1;
        }
        printf("%d\n", ans);
    }
    return 0;
}

 Building roads

这道题忘记输出-1导致wa了3发。啊这 （话说2-SAT好喜欢跟二分一起考啊）

题意：

给出n个农场和两个中转站s1,2，每个农场都必须连接一个中转站，且只能连一个，给出所有点的坐标，对应距离为曼哈顿距离（|xi-xj|+|yi-yj|），求如何建图能够使得其中所有点距离的最大值最小化。其中s1和s2之间有一条已有的路。

给出a个限制条件，这a个限制条件中的两个农场不能连接同一个中转站

给出b个限制条件，这b个限制条件中的两个农场必须连接同一个中转站

思路：首先对于最小化最大值类似的问题，我们很容易想到用二分答案的方法。

对应每个农场，要么连接s1，要么连接s2，那么对应建点：1~n表示点选择连接s1，n+1~2n表示点选择连接s2。

对于农场x，用x表示连接s1,用！x表示连接s2

（1）两个农场不能连接同一个中转站，建边（a, !b）,（b, !a），（！b, a）,（！a, b）

（2）两个农场必须连接同一个中转站，建边（a,  b）,（b,  a），（！b, ！a）,（！a,！ b）

对于二分出来的当前mid值，对应还有约束条件，找到矛盾边，然后继续建图

（1）对应两个点，如果其距离大于了mid，那么这个值不满足，直接退出。

（2）点i选择s1，点j选择s1    if(dis1[i]+dis1[j]>mid)      建边（i,! j）,（j, ! i）                                     i ,j 不能同时选择s1

（3）点i选择s1，点j选择s2    if(dis1[i]+dis2[j]+Dis1_2>mid)   建边（i, j），（! j, ! i）                       若i选择s1，则j不能选择s2；若j选择s2，i不能选择s1               

（4）点i选择s2，点j选择s2    if(dis2[i]+dis(2[j]>mid)     建边 (！i，j)，（！j，i）                               i, j 不能同时选择s2

（5）点i选择s2，点j选择s1    if(dis2[i]+dis1[j]+Dis1_2>mid)   建边(！i，！j)，（j，i）                      若i选择s2，则j不能选择s1；若j选择s1，i不能选择s2  

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
#define eps 1e-6
using namespace std;
const int maxn = 1e4 + 500;
int Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int t, m1, m2, n;
int s1x, s1y, s2x, s2y;
const int INF = 0x3f3f3f3f;
struct Node{
    int v, nex;
}edge[1000000+100];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

int x[maxn], y[maxn];
pair<int, int> e1[maxn], e2[maxn];
int dis(int x1, int y1, int x2, int y2){ return abs(x1-x2) + abs(y1-y2);}

bool check(int limt) {
    init();
    for (int i = 1; i <= m1; i ++) {
        int u = e1[i].first, v = e1[i].second;
        Add(u, v+n), Add(v, u+n);
        Add(u+n, v), Add(v+n, u);
    }
    for (int i = 1; i <= m2; i ++) {
        int u = e2[i].first, v = e2[i].second;
        Add(u, v), Add(v+n, u+n);
        Add(u+n, v+n), Add(v, u);
    }
    int s1_s2 = dis(s1x, s1y, s2x, s2y);
    for (int i = 1; i < n; i++) {
        for (int j = i+1; j <= n; j++) {
            int i_s1 = dis(x[i], y[i], s1x, s1y);
            int j_s1 = dis(x[j], y[j], s1x, s1y);
            int i_s2 = dis(x[i], y[i], s2x, s2y);
            int j_s2 = dis(x[j], y[j], s2x, s2y);
            if(limt < i_s1 + j_s1) //不能都选是
                Add(i, j+n), Add(j, i+n);
            if (limt < i_s2 + j_s2) //不能都选否
                Add(i+n, j), Add(j+n, i);
            if(limt < i_s1 + j_s2 + s1_s2) //不能同时i选是，j选否
                Add(i, j), Add(j+n, i+n);
            if(limt < i_s2 + j_s1 + s1_s2) //不能同时i选否，j选是
                Add(i+n, j+n), Add(j, i);
        }
    }
    for (int i = 1; i <= 2*n; ++i)//缩点
        if (!dfn[i]) Tarjan(i);
    for (int i = 1; i <= n; ++i) {//判断是否有解
        if (belong[i] == belong[i+n]) {//某个婚礼的 开始/结束 在同一个强连通分量中，无解
            return 0;
        }
        Opp[belong[i]] = belong[i+n]; //存一下超级点的的对立点
        Opp[belong[i+n]] = belong[i]; //反向也要存
    }
    return 1;
}

int main() {
    while (~scanf("%d%d%d", &n, &m1, &m2)) {
        scanf("%d%d%d%d", &s1x, &s1y, &s2x, &s2y);
        for (int i = 1; i <= n; ++ i)
            scanf("%d%d", &x[i], &y[i]);
        for (int i = 1; i <= m1; ++ i)
            scanf("%d%d", &e1[i].first, &e1[i].second);
        for (int i = 1; i <= m2; ++ i)
            scanf("%d%d", &e2[i].first, &e2[i].second);
        int L=0, R=INF, ans=INF;
        while (L <= R) {
            int mid = (L + R) / 2;
            //cout << mid << endl;
            if (check(mid)) {
                R = mid - 1;
                ans = min(ans, mid);
            } else L = mid + 1;
        }
        printf("%d\n", ans==INF?-1:ans);
    }
    return 0;
}

Eliminate the Conflict

题意：题意围绕“剪刀石头布”而展开，给出Bob的N(N <=10^5)次出法（1代表石头、2代表纸、3代表剪刀），Alice需要满足M(M <= 10^5)个条件，条件分两种：

            1、a b 0 第a次和第b次出法必须相同；

            2、a b 1 第a次和第b次出法必须不同；

       如果Alice在这N次对决中，没有一次输才算赢，问是否存在这样一种出法是的Alice获胜。

       题解：Alice的每次出法都有两种选择：要么和Bob出的一样，要么赢过Bob；将这两种出法拆成两个点，总共2N个点，然后根据M个条件建立有向边。

            1、  第a次和第b次出法必须相同，所以枚举第a次的两种情况和第b次的两种情况进行两两组合，如果出法不同则建边；

            2、  第a次和第b次出法必须不同，所以枚举第a次的两种情况和第b次的两种情况进行两两组合，如果出法相同则建边；

       建完边，求一次强连通判可行即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
#define eps 1e-6
using namespace std;
const int maxn = 1e5 + 500;
int Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int t, m, n;
const int INF = 0x3f3f3f3f;
struct Node{
    int v, nex;
}edge[100000+100];
int a[maxn][2];
int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

int x[maxn], y[maxn];
pair<int, int> e1[maxn], e2[maxn];
int dis(int x1, int y1, int x2, int y2){ return abs(x1-x2) + abs(y1-y2);}

bool solve() {
    for (int i = 1; i <= 2*n; ++i)//缩点
        if (!dfn[i]) Tarjan(i);
    for (int i = 1; i <= n; ++i) {//判断是否有解
        if (belong[i] == belong[i+n]) {//某个婚礼的 开始/结束 在同一个强连通分量中，无解
            return 0;
        }
        Opp[belong[i]] = belong[i+n]; //存一下超级点的的对立点
        Opp[belong[i+n]] = belong[i]; //反向也要存
    }
    return 1;
}

int main() {
    int T; scanf("%d", &T);
    for (int kase = 1; kase <= T; kase++) {
        scanf("%d%d", &n, &m);
        init();
        for (int i = 1; i <= n; i++) {
            scanf("%d", &a[i][0]);
            a[i][0] --;
            a[i][1] = (a[i][0] + 1) % 3;
        }
        for (int i = 1; i <= m; i++) {
            int u, v, val;
            scanf("%d%d%d", &u, &v, &val);
            if (!val) {
                if (a[u][0] != a[v][0]) Add(u, v+n), Add(v, u+n);
                if (a[u][0] != a[v][1]) Add(u, v), Add(v+n, u+n);
                if (a[u][1] != a[v][0]) Add(u+n, v+n), Add(v, u);
                if (a[u][1] != a[v][1]) Add(u+n, v), Add(v+n, u);
            }
            else {
                if (a[u][0] == a[v][0]) Add(u, v+n), Add(v, u+n);
                if (a[u][0] == a[v][1]) Add(u, v), Add(v+n, u+n);
                if (a[u][1] == a[v][0]) Add(u+n, v+n), Add(v, u);
                if (a[u][1] == a[v][1]) Add(u+n, v), Add(v+n, u);
            }
        }
        printf("Case #%d: %s\n", kase, solve()?"yes":"no");
    }
    return 0;
}

 Bit Magic

这道题主要是需要读懂题目意思。

题意：

求是否存在这样的数组a

使得b数组对应等式成立

问：

给定b数组，求是否有这样的a数组

思路：

对于每一个二进制位：

是否存在一个二进制位使得该式成立

然后2-sat 31次即可

（这里主要就是考察了建图模型4和1）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
#define eps 1e-6
using namespace std;
const int maxn = 1e3 + 500;
int Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int t, m, n;
const int INF = 0x3f3f3f3f;
struct Node{
    int v, nex;
}edge[500*2001];
int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

int b[maxn][maxn];
bool solve() {
    for (int i = 0; i < n; ++ i) {
        for (int j = i; j < n; ++ j) {
            if (i == j && b[i][j]) return 0;
            if (b[i][j] != b[j][i]) return 0;
        }
    }
    for (int k = 0; k < 31; ++k) { //枚举位数
        init();
        for (int i = 0; i < n; ++ i) {
            for (int j = i+1; j < n; ++ j) {
                if (i == j) continue;
                int val = b[i][j] & (1<<k);
                // +n代表1
                if ((i&1) && (j&1)) { // |
                    if (val) Add(i, j+n), Add(j, i+n); //选了0的话另一边一定要选1
                    else Add(i+n, i), Add(j+n, j); //0和1一定要选0
                }
                else if (!(i&1) && !(j&1)) {  // &
                    if (val) Add(i, i+n), Add(j, j+n); //0和1一定要选1
                    else Add(i+n, j), Add(j+n, i); //选了1的话另一边一定要选0
                }
                else { // ^
                    if (val) Add(i+n, j), Add(j+n, i), Add(i, j+n), Add(j, i+n);//一定要选不同的
                    else Add(i, j), Add(j, i), Add(i+n, j+n), Add(j+n, i+n);//一定要选相同的
                }
            }
        }
        for (int i = 0; i < 2*n; ++i)//缩点
            if (!dfn[i]) Tarjan(i);
        for (int i = 0; i < n; ++i) {//判断是否有解
            if (belong[i] == belong[i+n]) {
                return 0;
            }
            Opp[belong[i]] = belong[i+n];
            Opp[belong[i+n]] = belong[i];
        }
    }
    return 1;
}

int main() {
    while (~scanf("%d",&n)) {
        for (int i = 0; i < n; ++ i)
            for (int j = 0; j < n; ++ j)
                scanf("%d", &b[i][j]);
        puts(solve()?"YES":"NO");
    }
    return 0;
}

Map Labeler

这题和那道bomb挺像的，就是改成了正方形。建图可能需要想一想，其他的没啥了。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
#define eps 1e-6
using namespace std;
const int maxn = 1e4 + 500;
int Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int t, m1, m2, n;
int s1x, s1y, s2x, s2y;
const int INF = 0x3f3f3f3f;
struct Node{
    int v, nex;
}edge[1000000+100];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

int x[maxn], y[maxn];
pair<int, int> e1[maxn], e2[maxn];
int dis(int x1, int y1, int x2, int y2){ return abs(x1-x2) + abs(y1-y2);}

bool check(int val) {
    init();
    for(int i = 1; i <= n; ++i){
        for(int j = i + 1; j <= n; ++j){
            int dx = abs(x[i] - x[j]);
            int dy = abs(y[i] - y[j]);
            if(dx < val){
                if(dy < 2 * val){
                    if(dy >= val){
                        if(y[i] > y[j]) Add(i+n,j+n), Add(j,i);
                        else Add(j+n,i+n), Add(i,j);
                    }
                    else if(dy > 0){
                        if(y[i] > y[j]) Add(i,j+n), Add(j,j+n), Add(i+n,i), Add(j+n,i);
                        else Add(j,i+n), Add(i,i+n), Add(j+n,j), Add(i+n,j);
                    }
                    else Add(i,j+n), Add(j,i+n), Add(j+n,i), Add(i+n,j);

                }
            }
        }
    }
    for (int i = 1; i <= 2*n; ++i)//缩点
        if (!dfn[i]) Tarjan(i);
    for (int i = 1; i <= n; ++i) {//判断是否有解
        if (belong[i] == belong[i+n]) {//某个婚礼的 开始/结束 在同一个强连通分量中，无解
            return 0;
        }
        Opp[belong[i]] = belong[i+n]; //存一下超级点的的对立点
        Opp[belong[i+n]] = belong[i]; //反向也要存
    }
    return 1;
}

int main() {
    int T; scanf("%d", &T);
    while (T--) {
        init();
        scanf("%d", &n);
        for (int i = 1; i <= n; ++ i)
            scanf("%d%d", &x[i], &y[i]);
        int L=0, R=INF, ans=0;
        while (L <= R) {
            int mid = (L + R) / 2;
            //cout << mid << endl;
            if (check(mid)) {
                L = mid + 1;
                ans = max(ans, mid);
            } else R = mid - 1;
        }
        printf("%d\n", ans);
    }
    return 0;
}

Get Luffy Out

设有一把钥匙x，x表示选，~x表示不选.

如果有一对钥匙a，b，则a->~b，b->~a，即a，b不同时存在.

如果有一个门的所需要的钥匙是a，b,则~a->b，~b->a,即a，b不同时不存在.

二分查找答案判断

这道题用到了模型二和一

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
#define eps 1e-6
using namespace std;
const int maxn = 1e4 + 500;
int Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int t, m, n;
int s1x, s1y, s2x, s2y;
const int INF = 0x3f3f3f3f;
struct Node{
    int v, nex;
}edge[1000000+100];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

pair<int, int> key[maxn], door[maxn];

bool check(int val) {
    init();
     //两把钥匙只能选其中一把
    for (int i = 1; i <= n; ++ i) {
        int u = key[i].first, v = key[i].second;
        Add(u, v+2*n), Add(v, u+2*n);
    }
    //两把钥匙不能同时不选
    for (int i = 1; i <= val; ++ i) {
        int u = door[i].first, v = door[i].second;
        Add(u+2*n, v), Add(v+2*n, u);
    }

    for (int i = 1; i <= 4*n; ++i)//缩点
        if (!dfn[i]) Tarjan(i);
    for (int i = 1; i <= 2*n; ++i) {//判断是否有解
        if (belong[i] == belong[i+2*n]) {//某个婚礼的 开始/结束 在同一个强连通分量中，无解
            return 0;
        }
        Opp[belong[i]] = belong[i+2*n]; //存一下超级点的的对立点
        Opp[belong[i+2*n]] = belong[i]; //反向也要存
    }
    return 1;
}

int main() {
    while (~scanf("%d%d", &n, &m)) {
        if (!n && !m) break;
        for (int i = 1; i <= n; ++ i) {
            scanf("%d%d", &key[i].first, &key[i].second);
            key[i].first++, key[i].second++;
        }
        for (int i = 1; i <= m; ++ i) {
            scanf("%d%d", &door[i].first, &door[i].second);
            door[i].first++, door[i].second++;
        }

        int L=0, R=m, ans=0;
        while (L <= R) {
            int mid = (L + R) / 2;
            //cout << mid << endl;
            if (check(mid)) {
                L = mid + 1;
                ans = max(ans, mid);
            } else R = mid - 1;
        }
        printf("%d\n", ans);
    }
    return 0;
}

 Ikki's Story IV - Panda's Trick

题意就是：平面上，一个圆，圆的边上按顺时针放着n个点。现在要连m条边，比如a，b，
那么a到b可以从圆的内部连接，也可以从圆的外部连接。给你的信息中，每个点最多只会连接的一条边。
问能不能连接这m条边，使这些边都不相交。
1：每个边看成2个点：分别表示在内部连接和在外部连接，只能选择一个。计作点i和点i'
2：如果两条边i和j必须一个画在内部，一个画在外部（一个简单判断就可以）
那么连边：
i->j’, 表示i画内部的话，j只能画外部，即j’
j->i’，同理
i’->j，同理
j’->i，同理

难的地方可能就是判断是否相交了吧。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
#define eps 1e-6
using namespace std;
const int maxn = 1e4 + 500;
int Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int t, m, n;
int s1x, s1y, s2x, s2y;
const int INF = 0x3f3f3f3f;
struct Node{
    int v, nex;
}edge[1000000+100];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

pair<int, int> line[maxn];

bool check() {
    init();
    for(int i = 1; i <= m; i++) {
        for(int j = 1; j < i; j++) {
            int s1 = line[i].first, t1 = line[i].second,
                s2 = line[j].first, t2 = line[j].second;
            if((s1 > s2 && s1 < t2 && t1 > t2)
                || (s2 > s1 && s2 < t1 && t2 > t1))
            {
                Add(i, j + n), Add(j, i + n);
                Add(i + n, j), Add(j + n, i);
            }
        }
    }

    for (int i = 1; i <= 2*n; ++i)//缩点
        if (!dfn[i]) Tarjan(i);
    for (int i = 1; i <= n; ++i) {//判断是否有解
        if (belong[i] == belong[i+n]) {//某个婚礼的 开始/结束 在同一个强连通分量中，无解
            return 0;
        }
        Opp[belong[i]] = belong[i+n]; //存一下超级点的的对立点
        Opp[belong[i+n]] = belong[i]; //反向也要存
    }
    return 1;
}

int main() {
    while (~scanf("%d%d", &n, &m)) {
        for (int i = 1; i <= m; ++ i) {
            scanf("%d%d", &line[i].first, &line[i].second);
            line[i].first++, line[i].second++;
            if (line[i].first > line[i].second)
                swap(line[i].first, line[i].second);
        }
        puts(check()?"panda is telling the truth...":"the evil panda is lying again");
    }
    return 0;
}

 Wedding

这题比较麻烦、

【题意】：有一对新人结婚，邀请n对夫妇去参加婚礼。
有一张很长的桌子，人只能坐在桌子的两边，还要满
足下面的要求：1.每对夫妇不能坐在同一侧 2.n对夫妇
之中可能有通奸关系（包括男男，男女，女女），有通
奸关系的不能同时坐在新娘的对面，可以分开坐，可以
同时坐在新娘这一侧。如果存在一种可行的方案，输出
与新娘同侧的人。

 

求解的时候去选择和新郎同一侧的人，输出的时候换一下就是新娘同一侧的人。

如果i和j有奸情，则增加一条i到j',j到i'的边，

同时增加一条新娘到新郎的边，表示必须选新郎。

 

本题直接选新娘一边的容易错。因为新娘也可能有奸情，需要排除，具体可以见discuss

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn = 1e5+10;
int color[maxn], In[maxn], len[maxn], Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int n, m;
vector<int> G[maxn];//超级点就用vector来存边,方便些
struct Node{
    int v, nex;
}edge[maxn];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}
void Build_New() {
    for (int i = 1; i <= 2*n; ++ i) G[i].clear();
    for (int i = 1; i <= 2*n; ++i) {
        for(int j = head[i]; ~j; j = edge[j].nex){
            int v = edge[j].v;
            if (belong[i] == belong[v]) continue;
            G[belong[v]].push_back(belong[i]);//边要反着存
            In[belong[i]] ++;//统计入度
        }
    }
}
void topu() {
    memset(In, 0, sizeof(In));
    memset(color, -1, sizeof(color));
    //缩点之后建新图
    Build_New();
    queue<int> q;//拓扑排序的队列
    for (int i = 1; i <= sccNum; ++i)
        if (!In[i]) q.push(i); //入度为0的进队
    while (!q.empty()) {
        int v=q.front();
        q.pop();
        if(color[v] == -1) { // -1为未染色
            color[v] = 1;     //染为1
            color[Opp[v]] = 0; //对立点染为0
        }
        for (int i = 0; i < G[v].size(); ++i)  //依次减入度
            if (--In[G[v][i]] == 0) q.push(G[v][i]); //入度为0
    }
}
void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(In, 0, sizeof(In));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

int main() {
    while (~scanf("%d%d", &n, &m)) {
        if (!n && !m) break;
        init();
        char x1, y1; int x, y;
        for (int i = 1; i <= m; i++) {
            cin >> x >> x1 >> y >> y1;
            if (!x) x = n;
            if (!y) y = n;
            //w代表的1(+n), h代表0
            if(x1=='h' && y1=='h')    Add(x,y+n),Add(y,x+n); //如果选了xh跟yh不能同时选
            if(x1=='h' && y1=='w')    Add(x,y),Add(y+n,x+n); 
            if(x1=='w' && y1=='h')    Add(x+n,y+n),Add(y,x);
            if(x1=='w' && y1=='w')    Add(x+n,y),Add(y+n,x);
        }
        Add(2*n, n);
        for (int i = 1; i <= 2*n; ++i)//缩点
            if (!dfn[i]) Tarjan(i);
        int flag = 0;
        for (int i = 1; i <= n; ++i) {//判断是否有解
            if (belong[i] == belong[i+n]) {//无解
                flag = 1;
                break;
            }
            Opp[belong[i]] = belong[i+n]; //存一下超级点的的对立点
            Opp[belong[i+n]] = belong[i]; //反向也要存
        }
        if (flag) {
            puts("bad luck");
            continue;
        }
        topu();//Top排序
        for(int i=1;i<n;i++)//解的方式和上面一致。
        {
            if (color[belong[i]]==0) //0代表新郎的颜色
                cout<<i<<"h ";
            else                //1代表新娘的颜色
                cout<<i<<"w ";
        }
        cout<<endl;
    }
    return 0;
}

Katu Puzzle

这题其实跟那道位运算的差不多。听套路的。

  每个Xi就两种情况..并且必须选择一个..符合2-sat的模型..那剩下就是根据运算式构造边了...这里要进一步理解2-sat中一条有向边的涵义是选了起点就必须选终点..那剩下的就好办了一个一个分析...

                 x,y代表当前的式子未知数..x0为x选0的点..x1为x选1的点...y0,y1同样..

                 1、x AND y = 1 .. 表明x , y必须为1...所以不能选择x0,y0...这个东西要表示出来..就让选择x0,y0直接就自我矛盾..加边 ( x0,x1 ) , ( y0,y1 )

                 2、x AND y = 0 ..表明x,y至少有一个为0...那么加边 ( x1,y0 ) , ( y1,x0 )

                 3、x OR y = 1 ...表明x,y至少有一个味1..那么加边 ( x0,y1 ) , ( y0,x1 )

                 4、x OR y = 0..表明x,y都为0...所以让选择x1,y1就直接自矛盾 ( x1,x0 ) , ( y1,y0 )

                 5、x XOR y = 1..表明x,y不同..那么加边 ( x0,y1 ) , ( x1,y0 ) ,( y0,x1 ) , ( y1,x0 )

                 6、x XOR y = 0..表明x,y是相同的..那么加边 ( x0,y0 ) , ( x1,y1 ) ,( y0,x0 ) , ( y1,x1 )

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn = 1e5+10;
int color[maxn], In[maxn], len[maxn], Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int n, m;
vector<int> G[maxn];//超级点就用vector来存边,方便些
struct Node{
    int v, nex;
}edge[maxn];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(In, 0, sizeof(In));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

int main() {
    while (~scanf("%d%d", &n, &m)) {
        init();
        for (int i = 1; i <= m; i++) {
            int a, b, val;
            char str[10];
            scanf("%d%d%d%s", &a, &b, &val, str);
            a++, b++;
            if (strcmp(str, "AND") == 0) {
                if (val) Add(a, a+n), Add(b, b+n); //0和1一定要选1
                else Add(a+n, b), Add(b+n, a); //选了1的话另一边一定要选0
            }
            else if (strcmp(str, "OR") == 0) {
                if (val) Add(a, b+n), Add(b, a+n); //选了0的话另一边一定要选1
                else Add(a+n, a), Add(b+n, b); //0和1一定要选0
            }
            else if (strcmp(str, "XOR") == 0) {
                if (val) Add(a+n, b), Add(b+n, a), Add(a, b+n), Add(b, a+n);//一定要选不同的
                else Add(a, b), Add(b, a), Add(a+n, b+n), Add(b+n, a+n);//一定要选相同的
            }
        }
        for (int i = 1; i <= 2*n; ++i)//缩点
            if (!dfn[i]) Tarjan(i);
        int flag = 0;
        for (int i = 1; i <= n; ++i) {//判断是否有解
            if (belong[i] == belong[i+n]) {//无解
                flag = 1;
                break;
            }
            Opp[belong[i]] = belong[i+n]; //存一下超级点的的对立点
            Opp[belong[i+n]] = belong[i]; //反向也要存
        }
        puts(flag?"NO":"YES");
    }
    return 0;
}

Perfect Election

就是读懂题意照题意模拟就好了。

就是注意数组可能要开大一点。还有不能用cin （会TLE)

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn = 1e4+10;
int Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int n, m;
struct Node{
    int v, nex;
}edge[4000000+100];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(instack, 0, sizeof(instack));
    memset(head, -1, sizeof(head));
}

int main() {
    while (~scanf("%d%d", &n, &m)) {
        init();
        for (int i = 1; i <= m; i++) {
            int a, b;
            scanf("%d%d", &a, &b);
            if (a > 0 && b > 0)
                Add(a+n, b), Add(b+n, a);
            else if (a > 0 && b < 0)
                Add(a+n, -b+n), Add(-b, a);
            else if (a < 0 && b > 0)
                Add(-a, b), Add(b+n, -a+n);
            else if (a < 0 && b < 0)
                Add(-a, -b+n), Add(-b, -a+n);
        }
        for (int i = 1; i <= 2*n; ++i)//缩点
            if (!dfn[i]) Tarjan(i);
        int flag = 0;
        for (int i = 1; i <= n; ++i) {//判断是否有解
            if (belong[i] == belong[i+n]) {//无解
                flag = 1;
                break;
            }
        }
        puts(flag?"0":"1");
    }
    return 0;
}

Get Luffy Out *

这道题好像是对搜索解法的限制加强。对于2-SAT并没有什么变化。直接交弱化版的代码就过了。（好水。

题意：Get Luffy Out的加强版，每个钥匙有可能出现在不同的钥匙对中。

       题解：首先还是二分答案。然后拆点，总共2N把钥匙，拆成4N个点，分别表示这个钥匙的取或不取。然后两种情况建边：

            1．对于每对钥匙(x, y)，如果x取，则y不取；同理，如果y取，则x不取；

            2．对于每扇门(a, b)，如果a不取，则b必须取；如果b不取，则a必须取；

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
#define eps 1e-6
using namespace std;
const int maxn = 1e4 + 500;
int Opp[maxn];
int sta[maxn], belong[maxn], dfn[maxn], low[maxn];
int sccNum = 0, top=0, id=0;
bool instack[maxn];
int t, m, n;
int s1x, s1y, s2x, s2y;
const int INF = 0x3f3f3f3f;
struct Node{
    int v, nex;
}edge[1000000+100];

int head[maxn], cnt;

inline void Add(int u,int v) {
    edge[cnt] = {v, head[u]};
    head[u] = cnt++;
}

void Tarjan(int u) {
    int v;
    dfn[u] = low[u] = ++id;
    sta[++top] = u, instack[u] = 1;
    for (int i = head[u]; ~i; i = edge[i].nex) {
        v = edge[i].v;
        if(!dfn[v]) {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instack[v])
            low[u] = min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccNum;
        do {
            v = sta[top--];
            instack[v] = 0;
            belong[v] = sccNum;
        } while (v != u);
    }
}

void init() {
    cnt = id = sccNum = top = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(instack, 0, sizeof(instack));
    memset(Opp, 0, sizeof(Opp));
    memset(head, -1, sizeof(head));
}

pair<int, int> key[maxn], door[maxn];

bool check(int val) {
    init();
     //两把钥匙只能选其中一把
    for (int i = 1; i <= n; ++ i) {
        int u = key[i].first, v = key[i].second;
        Add(u, v+2*n), Add(v, u+2*n);
    }
    //两把钥匙不能同时不选
    for (int i = 1; i <= val; ++ i) {
        int u = door[i].first, v = door[i].second;
        Add(u+2*n, v), Add(v+2*n, u);
    }

    for (int i = 1; i <= 4*n; ++i)//缩点
        if (!dfn[i]) Tarjan(i);
    for (int i = 1; i <= 2*n; ++i) {//判断是否有解
        if (belong[i] == belong[i+2*n]) {//某个婚礼的 开始/结束 在同一个强连通分量中，无解
            return 0;
        }
        Opp[belong[i]] = belong[i+2*n]; //存一下超级点的的对立点
        Opp[belong[i+2*n]] = belong[i]; //反向也要存
    }
    return 1;
}

int main() {
    while (~scanf("%d%d", &n, &m)) {
        if (!n && !m) break;
        for (int i = 1; i <= n; ++ i) {
            scanf("%d%d", &key[i].first, &key[i].second);
            key[i].first++, key[i].second++;
        }
        for (int i = 1; i <= m; ++ i) {
            scanf("%d%d", &door[i].first, &door[i].second);
            door[i].first++, door[i].second++;
        }

        int L=0, R=m, ans=0;
        while (L <= R) {
            int mid = (L + R) / 2;
            //cout << mid << endl;
            if (check(mid)) {
                L = mid + 1;
                ans = max(ans, mid);
            } else R = mid - 1;
        }
        printf("%d\n", ans);
    }
    return 0;
}

2-SAT做了这么多题目我发现。他其实跟差分约束真的差不多。就是需要从题目中抽象出限制关系。

之后对有向边有了更深入的理解。

U --> V 代表的时如果选了U就一定要选V。这点很重要。而不能代表其他的意思。（分析题目也可以从这一点出发。

好像图论都是抽象出一个关系之后用图论方法去解决就好了。（图论真奇妙呀