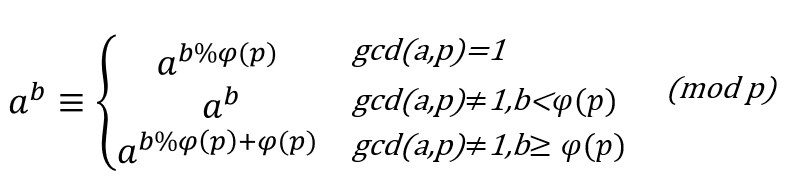定义
对正整数n,欧拉函数是小于或等于n的正整数中与n互质的数的数目。此函数以其首名研究者欧拉命名,它又称为Euler's totient function、φ函数、欧拉商数等。例如φ(8)=4,因为1,3,5,7均和8互质。
内容
通式:
其中p1, p2……pn为x的所有质因数,x是不为0的整数。
性质
① n的所有质因子之和是φ(n)*n/2。
② 若m,n互质,φ(m*n)=φ(m)*φ(n)。(欧拉函数是积性函数)
③ 若n为奇数,φ(2n)=φ(n)
④ 若n为质数,则φ(n)=n-1
⑤ 若n>2,则φ(n)是偶数。
⑥ 若p为质数,
⑦ 令a为N的质因子,则
若(N%a==0&&(N/a)%a==0) 则有: φ(N)=φ(N/a)*a
若(N%a==0&&(N/a)%a!=0) 则有: φ(N)=φ(N/a)*(a-1)
实现
根据公式
int Euler(int n)
{
int res=n;
for(int i=2;i*i<=n;i++)
{
if(n%i==0)
{
res=res/i*(i-1);
while(n%i==0) n/=i;
}
}
if(n>1) res=res/n*(n-1);
return res;
}
埃拉托斯特尼筛求欧拉函数
int phi[maxn];
void euler()
{
for(int i=2;i<maxn;i++)
{
if(phi[i]) continue;
for(int j=i;j<maxn;j+=i)
{
if(!phi[j]) phi[j]=j;
phi[j]=phi[j]/i*(i-1);
}
}
}
欧拉筛求欧拉函数
int phi[maxn],prime[maxn],top;
bool isprime[maxn];
void euler()
{
phi[1]=1;
memset(isprime,0,sizeof(isprime));
for(int i=2;i<=maxn;i++)
{
if(!isprime[i])
{
prime[top++]=i;
phi[i]=i-1;
}
for(int k=0;k<top&&i*prime[k]<=maxn;k++)
{
isprime[i*prime[k]]=1;
if(i%prime[k]==0)
{
phi[i*prime[k]]=phi[i]*prime[k];
break;
}
else phi[i*prime[k]]=phi[i]*(prime[k]-1);
}
}
}
欧拉降幂