数据结构 二分查找

　　二分查找，即折半查找，仅适用于有序的顺序表。基本思想：将给定值key与表中中间位置元素比较，如果相等则查找成功并返回该元素的存储位置，否则key只能在前半部分或后半部分中（例如，顺序表升序排列时，如果key大于中间元素，那么key只能在后半部分）。在缩小的范围内继续上述过程，直到找到或者确定表中没有key。

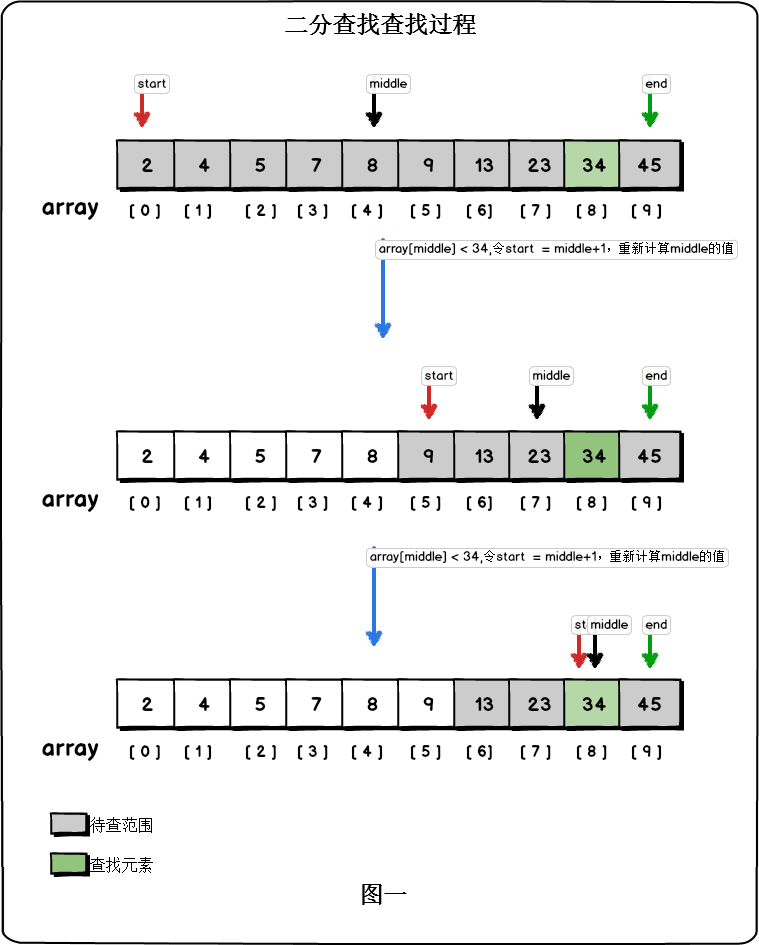
　　在数组{2，4，5，7，8，9，13，23，34，45}中查找元素34，过程见下图：

　　

public class BinarySearch {
    public static int binarySearch(int[] arr, int key) {
        if (arr == null || arr.length == 0) {
            return -1;
        }
        
        int low = 0, high = arr.length - 1;
        // 二分查找
        while (low <= high) {
            int mid = (low + high) >> 1;
            // 1 如果找到
            // 2 如果在前半部分
            // 3 如果在后半部分
            if (arr[mid] == key) {
                return mid;
            } else if (arr[mid] > key) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        
        // 没有找到
        return -1;
    }
}

　　测试用例：

import static org.junit.Assert.assertEquals;

import org.junit.Test;

public class BinarySearchTest {

    @Test
    public void test() {
        int[] arr = {2, 4, 5, 7, 8, 9, 13, 23, 34, 45};
        assertEquals(8, BinarySearch.binarySearch(arr, 34));
    }

}

　　测试结果：

　　

　　二分查找的过程可以用判定树来描述，树中每个圆形结点表示一个元素，结点中的值是元素值。树中最下面的叶子结点是方形的，表示查找不成功的情况。查找成功时的查找长度为从根结点到目的结点的路径上的结点数，而查找不成功时的查找长度为从根结点到对应失败结点的父结点的路径上的结点数。每个结点值大于左孩子结点值，小于或等于右孩子结点值。如果有序序列有n个元素，那么对应的判定树有n个圆形的非叶子结点和n+1个方形的叶子结点。

　　

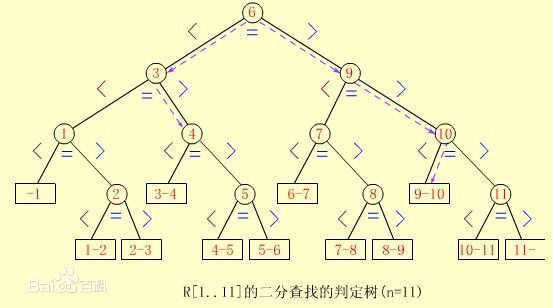
　　二分查找给定值的比较次数不会超过树的高度。平均情况下二分查找的时间复杂度为O(log₂n)，效率高于顺序查找。因为二分查找需要方便地定位查找区域，所以二分查找适合于线性表的顺序存储结构，不适合链式存储结构，要求元素有序排列。

　　

　　lowerBound

　　返回有序序列中第一个大于或等于给定值的元素位置，如果不存在则返回序列右边界+1。

public static int lowerBound(int[] arr, int key) {
    if (arr == null || arr.length == 0) {
        return -1;
    }
    
    int low = 0, high = arr.length;
    while (low < high) {
        int mid = (low + high) >> 1;
        if (arr[mid] >= key) {
            high = mid;
        } else {
            low = mid + 1;
        }
    }
    
    return high;
}

　　测试用例：

@Test
public void test1() {
    int[] arr = {2, 4, 5, 7, 8, 9, 13, 23, 34, 34};
    assertEquals(8, BinarySearch.lowerBound(arr, 34));
}

　　测试结果：

　　

　　upperBound

　　返回有序序列中第一个大于给定值的元素位置，如果不存在则返回序列右边界+1。

public static int upperBound(int[] arr, int key) {
    if (arr == null || arr.length == 0) {
        return -1;
    }
    
    int low = 0, high = arr.length;
    while (low < high) {
        int mid = (low + high) >> 1;
        if (arr[mid] > key) {
            high = mid;
        } else {
            low = mid + 1;
        }
    }
    
    return high;
}

　　测试用例：

@Test
public void test2() {
    int[] arr = {2, 4, 5, 7, 8, 9, 13, 23, 34, 37};
    assertEquals(9, BinarySearch.upperBound(arr, 34));
}

　　测试结果：

　　

　　参考资料

　　《2017年数据结构联考复习指导》 P233-234

　　数据结构图文解析之：二分查找及与其相关的几个问题解析

　　判定树

　　二分查找求上、下界