(1)进制转换
十进制转二进制
十进制数除2取余法,即十进制数除2,余数为权位上的数,得到的商值继续除2,依此步骤继续向下运算直到商为0为止。

运用短除法取余数,从下往上。
十进制转二进制小数
乘二取整数,用小数计算。
从上往下

二进制转十六进制
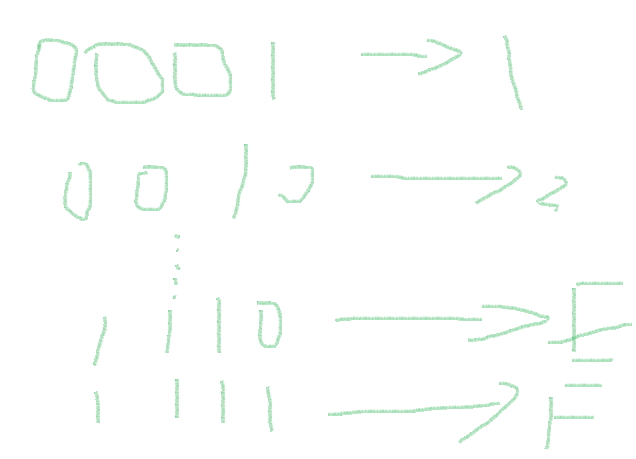
以小数点为分界,四位一组,一一对应。
十六进制转二进制
将二转十六反过来,一一对应。
二进制转八进制

以小数点为分界,三位一组,一一对应。
八进制转二进制
将二进制转八进制翻转。
x进制转十进制
根据位的高低a1*x^y.
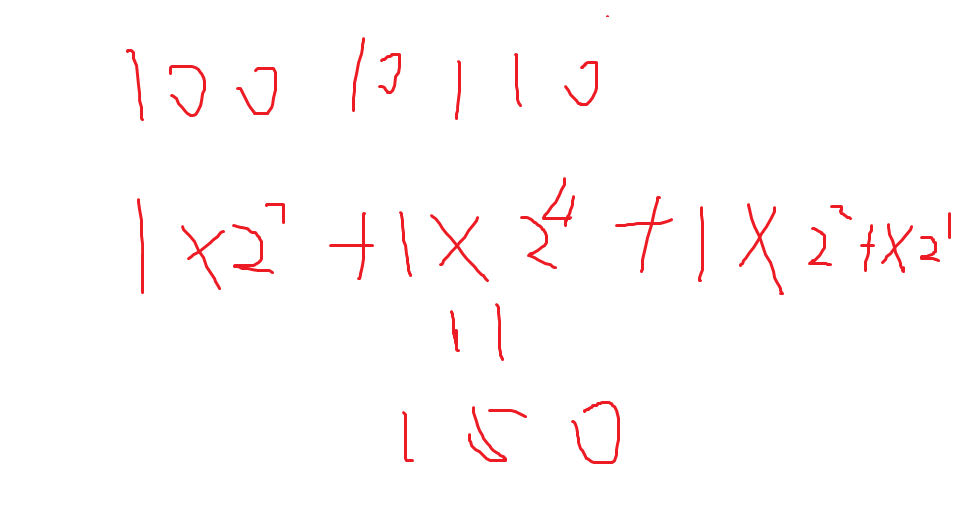
(2)位运算摘自 http://www.cnblogs.com/llllllpppppp/p/7652380.html
与(按位与& 逻辑与∧) 11取1 其它取0
或(按位或| 逻辑或∨) 00取0 其它取1
异或(按位异或^) 一样取0 不一样取1
取反(按位取反~ 逻辑取反﹁或!) 1变0,0变1
优先级:~ > & > ^ > |
位运算:
对于两个数进行按位运算时,先将两个数转化为二进制(小数点对齐),然后将每一位都进行逻辑运算(注意空位补0)
比如,计算21^2
先转换为二进制
21=(10101)2
2=(10)2
然后按位进行逻辑异或运算
10101
^ 10
————
10111
最后得出结果(10111)2=23
逻辑运算:
判断逻辑运算式的真假值时,把数带进去算一下就好了
例:A=true,B=false,C=false,D=true时
(A∧B)∨(C∧D)=0
((A∧B)∨C)∧D=0
A∧((B∨C)∨D)=1
(A∧(B∨C))∨D=1
(A∨B)∧(C∨D)=1
遇到这种题细心计算就好了
(3)八大排序
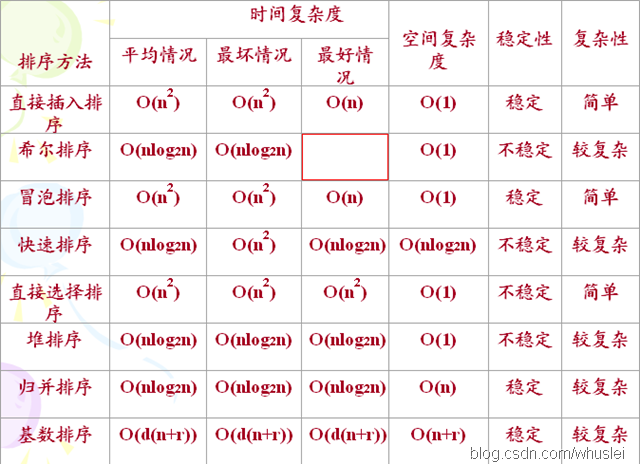
转自http://blog.csdn.net/whuslei/article/details/6442755/
(4)遍历
例子

先序遍历
原则 从根节点开始,能左则左,不能就往右。
样例:1 2 4 5 3 6
中序遍历
原则 先找到最左,然后他的父亲节点,然后往右。左中右
样例:4 2 5 1 6 3
后序遍历
原则 先找到最左,然后右,然后父亲节点 。 左右中
样例:4 5 2 6 3 1
(5)表达式
前缀表达式
样例:+3*2+5 12
方法:依次进栈,当遇到连着的两个数就开始运算,用上一个运算符进行运算,结果进栈。
样例+3*2 17 --> +3 34 --> 37
中缀表达式
就是普通的表达式,直接运算。
后缀表达式
样例:3 4 + 5 × 6 -
样例:7*5-6 35-6 29
(6)原码 反码 补码
原码, 反码和补码的概念 对于一个数, 计算机要使用一定的编码方式进行存储. 原码, 反码, 补码是机器存储一个具体数字的编码方式。
原码
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制
1 对应 0000 0001 第一个0代表它是正数
-1 对应 1000 0001 第一个1代表它是负数
第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是
1111 1111 到 0111 1111
127 到 -127
这是最容易理解的一种方式
反码
反码的表示方法是:
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变,其余各个位取反.
再举个例子
1 对应 0000 0001 反转后为 0000 0001
-1 对应 1000 0001 反转后为 1111 1110 第一位符号位不变
如果一个数是负数,就将它转化成原码,再反转
补码
补码的表示方法是:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
还是举个例子
+1 = [00000001]原 = [00000001]反 = [00000001]补 正数不变
-1 = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码,再转化成反码,再加一,计算其数值。
零的特殊
发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0.
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原
这样 1000 0000就可以用来表示-128.
只用0000 0000来表示0
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
物尽其用嘛
(7)拓扑排序
对一个有向无环图G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若u的入度小于v的入度,则u在线性序列中出现在v之前。
注意:
1)只有有向无环图才存在拓扑序列
2)对于一个有向无环图,可能存在多个拓扑序列
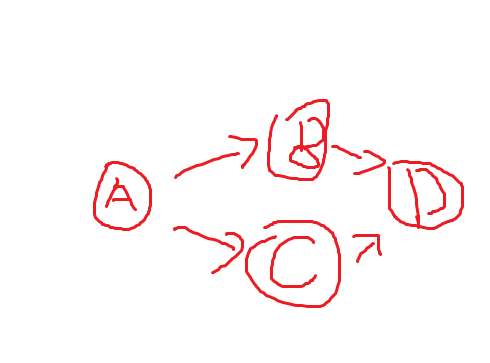
对此样例,有两种情况
1 A B C D
2 A C B D
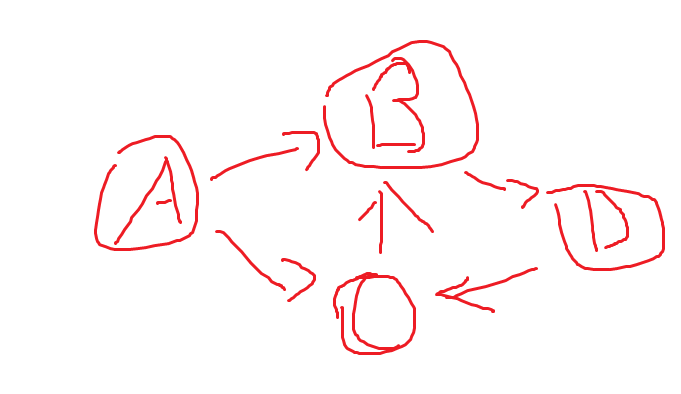
对此样例,不存在拓扑排序,因为他有自环。
注意:
拓扑序列中的第一个节点一定是入度为零的点。
万万要记住
(8)指针
int *a;
int b;
a=&b;
*取地址中的内容
&取地址
死记就行