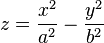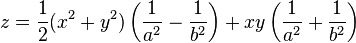双曲抛物面又称马鞍面,它在笛卡儿坐标系中的方程为：
其中x、y、z是平面直角坐标系三个坐标轴方向上的变量，a、b是常数。
本文将展示几种生成双曲抛物面算法和切图.使用自己定义语法的脚本代码生成数学图形.相关软件参见:数学图形可视化工具,该软件免费开源.QQ交流群: 367752815
(1)
vertices = dimension1:64 dimension2:64 x = from (-4) to (4) dimension1 z = from (-4) to (4) dimension2 y = x*x - z*z
(2)参数方程表示
#y = x*x/a/a - z*z/b/b vertices = dimension1:64 dimension2:64 u = from (-3) to (3) dimension1 v = from (-3) to (3) dimension2 a = rand2(0.5, 2) b = rand2(0.5, 2) x = a*(u + v) z = b*(u - v) y = 2*u*v
(3)三角函数表示
vertices = D1:64 D2:64 u = from (0) to (2*PI) D1 v = from (0) to (3) D2 a = rand2(0.5, 1) x = v*sin(u) z = v*cos(u) y = a*v*v*sin(u*2)
(4)乘法表示
如果把双曲抛物面
顺着+z的方向旋转π/4的角度，则方程为：
如果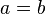
，则简化为：
.
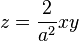最后，设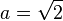
，我们可以看到双曲抛物面
.
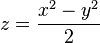与以下的曲面是全等的：
因此它可以视为乘法表的几何表示。
vertices = dimension1:64 dimension2:64 x = from (-4) to (4) dimension1 z = from (-4) to (4) dimension2 y = x*z
