第17届科大讯飞杯 J-斐波那契和 （玄学 BM）

题目：传送门

题意

 思路

明显的递推式，可以用 BM

其他思路：To

 

题解思路：

 

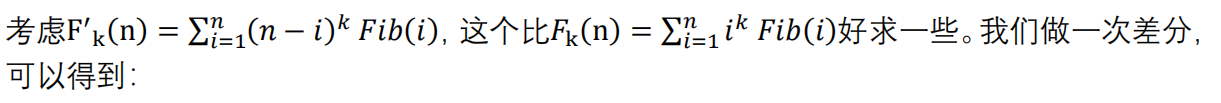
#include <bits/stdc++.h>
#define LL long long
#define ULL unsigned long long
#define UI unsigned int
#define mem(i, j) memset(i, j, sizeof(i))
#define rep(i, j, k) for(int i = j; i <= k; i++)
#define dep(i, j, k) for(int i = k; i >= j; i--)
#define pb push_back
#define make make_pair
#define INF 0x3f3f3f3f
#define inf LLONG_MAX
#define PI acos(-1)
#define fir first
#define sec second
#define lb(x) ((x) & (-(x)))
#define dbg(x) cout<<#x<<" = "<<x<<endl;
using namespace std;

typedef vector<int> VI;
typedef pair<int, int> PII;
const LL mod =  998244353;
LL ksm(LL a, LL b) {
    LL ans = 1;
    a %= mod;
    assert(b >= 0);
    for(; b; b >>= 1) {
        if(b & 1) ans = ans * a % mod;
        a = a * a % mod;
    }
    return ans;
}
LL n;
const int N = 10010;
LL res[N], base[N], _c[N], _md[N];
vector<int> Md;
void mul(LL *a, LL *b, int k) {
    rep(i, 0, k + k - 1) _c[i] = 0;
    rep(i, 0, k - 1) if(a[i]) rep(j, 0, k - 1) _c[i + j] = (_c[i + j] + a[i] * b[j]) % mod;
    dep(i, k, k + k - 1) if(_c[i])
        rep(j, 0, (int)Md.size() - 1) _c[i - k + Md[j]] = (_c[i - k + Md[j]] - _c[i] * _md[Md[j]]) % mod;
    rep(i, 0, k - 1) a[i] = _c[i];
}
int slove(LL n, VI a, VI b) {/// a 系数 b 初值 b[n+1]=a[0]*b[n]+...
    LL ans = 0, pnt = 0;
    int k = a.size();
    assert((int)a.size() == (int)b.size());
    rep(i, 0, k - 1) _md[k - 1 - i] = -a[i]; _md[k] = 1;
    Md.clear();
    rep(i, 0, k - 1) if(_md[i] != 0) Md.pb(i);
    rep(i, 0, k - 1) res[i] = base[i] = 0;
    res[0] = 1;
    while((1LL << pnt) <= n) pnt++;
    dep(p, 0, pnt) {
        mul(res, res, k);
        if((n >> p) & 1) {
            dep(i, 0, k - 1) res[i + 1] = res[i]; res[0] = 0;
            rep(j, 0, (int)Md.size() - 1) res[Md[j]] = (res[Md[j]] - res[k] * _md[Md[j]]) % mod;
        }
    }
    rep(i, 0, k - 1) ans = (ans + res[i] * b[i]) % mod;
    if(ans < 0) ans += mod;
    return ans;
}
VI BM(VI s) {
    VI C(1, 1), B(1, 1);
    int L = 0, m = 1, b = 1;
    rep(n, 0, (int)s.size() - 1) {
        LL d = 0;
        rep(i, 0, L) d = (d + (LL)C[i] * s[n - i]) % mod;
        if(d == 0) ++m;
        else if(2 * L <= n) {
            VI T = C;
            LL c = mod - d * ksm(b, mod - 2) % mod;
            while((int)C.size() < (int)B.size() + m) C.pb(0);
            rep(i, 0, (int)B.size() - 1) C[i + m] = (C[i + m] + c * B[i]) % mod;
            L = n + 1 - L; B = T; b = d; m = 1;
        } else {
            LL c = mod - d * ksm(b, mod - 2) % mod;
            while((int)C.size() < (int)B.size() + m) C.pb(0);
            rep(i, 0, (int)B.size() - 1) C[i + m] = (C[i + m] + c * B[i]) % mod;
            ++m;
        }
    }
    return C;
}
int gao(VI a, LL n) {
    VI c = BM(a);
    c.erase(c.begin());
    rep(i, 0, (int)c.size() - 1) c[i] = (mod - c[i]) % mod;
    return slove(n, c, VI(a.begin(), a.begin() + (int)c.size()));
}

LL F[N], f[N];

int k;

int main() {
    /*push_back 进去前 8~10 项左右、最后调用 gao 得第 n 项*/
    vector<int> v;

    scanf("%lld %d", &n, &k);

    f[1] = 1; f[2] = 1;

    F[1] = 1; F[2] = ksm(2, k) + f[1];

    v.pb(F[1]); v.pb(F[2]);

    rep(i, 3, 10000) {

        f[i] = (f[i - 1] + f[i - 2]) % mod;

        F[i] = (ksm(i, k) * f[i] % mod + F[i - 1]) % mod;

        v.pb(F[i]);

    }

    printf("%lld
", gao(v, n - 1) % mod);

}