树形DP
树形DP:建立在树上的动态规划
一般有两种传递方式:根→叶或叶→根
前者出现在换根DP中,一般操作是求出某一个点的最优解,再通过这一个点推知其他点的最优解。
后者是树形DP的常见形式,一般树形DP都是在叶子向根转移上。
一般状态都是f[x][...]表示x的子树中如何如何
POJ_3342_Party at Hali-Bula_树形DP
题目大意:没有上司的舞会,不存在选了连续两个点的情况,求最多选多少人。
题解:最裸的树形DP,直接状态,f[i][0]表示没选这个点,子树中最多选了多少个点。f[i][1]表示这个点选了,子树中最多选多少个点,之后每次max(f[son][0],f[son][1])更新f[x][0],之后f[son][0]更新f[x][1]
BZOJ_1864_[Zjoi2006]三色二叉树_树形DP
题目大意:
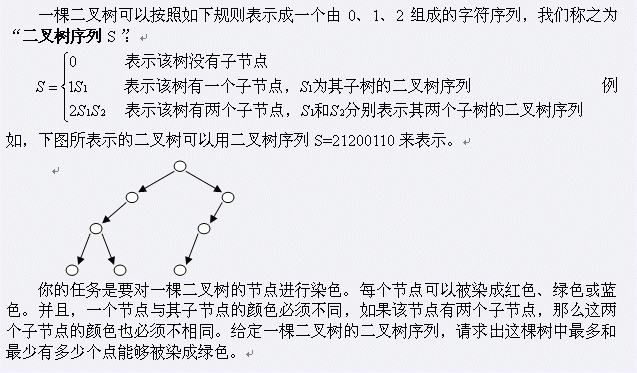
话说这道题的难点不在于树形DP啊...而是怎么把给你的东西转化成树啊...
树形DP很显然,f[x][1]表示这个点染成绿色的子树最大值,f[x]][0]表示没有染成绿色的子树最大值,(没有必要知道到底染成什么颜色,因为必定存在有解情况。)之后,直接转移一下。转移方程同上。
VIJOS P1144 小胖守皇宫
题目大意:
题意: 有一颗树, 每个节点是一个宫殿, 并且有个花费。 然后要驻扎人。 如果一个节点进驻了, 相邻的点,都会被监控。 问监控所有节点的最少花费。
相对于前两道题稍微复杂了一些。状态:f[x][0]表示x这个节点由儿子守的子树最小花费,f[x][1]表示这个点由自己守的子树最小花费,f[x][2]表示这个点由父亲守的子树最小花费。
之后转移就直接考虑一下那些状态全覆盖,那么就是f[x][1]可以从f[to][0,1,2]转移来,因为不论是哪一个,都满足要求,f[x][2]可以从f[to1][0,1]转移来,因为这两个也满足每一个节点都被守好了,而f[x][0]相对复杂一些,因为儿子节点只需要有一个守卫即可,那么我们考虑直接让f[x][0]从f[x][2]转移来,也就是在儿子节点中选择一个守卫与不守卫的差最小的一个。之后常规操作转移即可。
BZOJ_1060_时态同步_树形DP
题目大意:
给你一颗树,每次可以增加某一条路的长度,最后让所有根到叶子节点等长,求最小次数。
很显然,这是一个树形DP直接贪心的将所有子节点的距离改变成同一个,之后将子节点信息上传即可。
BZOJ_1040_[ZJOI2008]骑士_树形DP
题目大意:
给你一个基环树森林,之后选择若干个互相不直接相连的点,使权值最大。
树形DP比较显然,相对的来说就这是一类题型,基环树DP,找到每一个环,之后拆环分别DP最后合并答案即可。f[i][0]表示没选,f[i][1]表示选了,之后转移同上,每一个环有两种情况,找到环上任意一个边,断开,分别讨论两个都没选,选一个的情况,之后合并。
BZOJ_3037_创世纪_树形DP
题目大意:
给你n个点,每个点有一个父亲,求选择最大权值满足每个节点都有一个儿子不选。
同上,也是一个基环树DP,满足每个点都有一个入边,并且一共n个边,则必定为一个基环树。考虑状态,类似小胖守皇宫,但不太相同,f[x][0]表示这个点不选的子树最大权值和,f[x][1]表示这个点选的子树最大权值和,之后每次转移的时候找到一个儿子节点中f[x][0]-f[x][1]最大的,之后来更新f[x][1],其他的直接贪心的要最大值即可,另外针对每个环,将其拆开分别讨论,作为子节点的分别讨论选与不选,而作为父节点的直接dfs一遍,求出对应的状态即可,最后答案+=max(f[son][1],f[son][0]),注意后者包含f[x][1]的情况。
BZOJ_1827_[Usaco2010 Mar]gather_奶牛大集会
题目大意:
给你一棵树,问以某一点为根的时候,所有点深度*点权的和最小
另一类树形DP,换根DP,一般这类题目都是给你一个树,之后问你所有点的信息,这个时候,暴力求是N^2的,但是可以以任意节点为根节点,之后求出根节点的值,之后再把信息从父节点→子节点转移求出对应答案即可。
这个题,先求出1为根的情况,之后每次传递给子节点。
BZOJ_1131_[POI2008]Sta
题目大意:
给你一颗树,之后问以某一个点为根的时候,所有点的深度和最小。
树形DP,直接转移,每次父亲节点,减去这个子节点的贡献,之后传递给子节点即可。