实验环境:win10,VC++ 6.0 使用语言:C/C++
实验内容一:编写程序,完成二叉树的先序创建、先序遍历、中序遍历和后序遍历等操作
Binary.h
1 #include<iostream> 2 #include<stdlib.h> 3 #include<stack> 4 #include<queue> 5 using namespace std; 6 7 typedef char ElemType; 8 9 typedef struct BiTNode 10 { 11 ElemType data;//数据域 12 struct BiTNode *lchild, *rchild;//左孩子和右孩子 13 }BiTNode, *BiTree; 14 15 void CreateBiTree(BiTree *T);//创建二叉树,以先序遍历的方式进行输入和创建工作 16 void operation1(ElemType ch);//表示对遍历到的结点数据进行的处理操作,此处操作是将树结点前序遍历输出 17 void operation2(ElemType ch, int level);//此处在输出的基础上,并输出层数 18 void PreOrderTraverse(BiTree T, int level);//递归方式先序遍历二叉树 19 void InOrderTraverse(BiTree T,int level);//递归方式中序遍历二叉树 20 void PostOrderTraverse(BiTree T,int level);//递归方式后序遍历二叉树 21 void PreOrder(BiTree T);//非递归方式先序遍历 22 void InOrder(BiTree T);//非递归中序遍历 23 void PostOrder(BiTree T);//非递归后序遍历 24 void LevelOrder(BiTree T);//层次遍历
Binary.cpp
#include"Bianry.h" //根据试验要求,用先序创建的方式进行构建二叉树 //邹老师代课时建议我们加上层次遍历,希望李老师喜欢哈哈 void CreateBiTree(BiTree *T) { ElemType ch; cin >> ch; if (ch == '#') *T = NULL; else { *T = (BiTree)malloc(sizeof(BiTNode)); (*T)->data = ch;//生成结点 CreateBiTree(&(*T)->lchild);//构造左子树 CreateBiTree(&(*T)->rchild);//构造右子树 } } //先序遍历 void operation1(ElemType ch) { cout << ch << " "; } //此处在输出的基础上,并输出层数 void operation2(ElemType ch, int level) { cout << ch << "在第" << level << "层" << " "; } //先序遍历二叉树(递归方式) void PreOrderTraverse(BiTree T, int level) { if (T == NULL) return; operation1(T->data); //operation2(T->data, level); //可输出层数 PreOrderTraverse(T->lchild, level + 1); PreOrderTraverse(T->rchild, level + 1); } //中序遍历二叉树(递归方式) void InOrderTraverse(BiTree T,int level) { if(T==NULL) return; InOrderTraverse(T->lchild,level+1); operation1(T->data); //operation2(T->data, level); //可输出层数 InOrderTraverse(T->rchild,level+1); } //后序遍历二叉树(递归方式) void PostOrderTraverse(BiTree T,int level) { if(T==NULL) return; PostOrderTraverse(T->lchild,level+1); PostOrderTraverse(T->rchild,level+1); operation1(T->data); //operation2(T->data, level); //可输出层数 } /* 思路:将T入栈,遍历左子树;遍历完左子树返回时,栈顶元素应为T,出栈,再先序遍历T的右子树。*/ void PreOrder(BiTree T){ stack<BiTree> stack; //p是遍历指针 BiTree p = T; //p不为空或者栈不空时循环 while (p || !stack.empty()) { if (p != NULL) { //存入栈中 stack.push(p); //对树中的结点进行操作 operation1(p->data); //遍历左子树 p = p->lchild; } else { //退栈 p = stack.top(); stack.pop(); //访问右子树 p = p->rchild; } } } //中序遍历(非递归) void InOrder(BiTree T) { stack<BiTree> stack; //p是遍历指针 BiTree p = T; //p不为空或者栈不空时循环 while (p || !stack.empty()) { if (p != NULL) { //存入栈中 stack.push(p); //遍历左子树 p = p->lchild; } else { //退栈 p = stack.top(); operation1(p->data); //对树中的结点进行操作 stack.pop(); //访问右子树 p = p->rchild; } } } //后序遍历(非递归) typedef struct BiTNodePost{ BiTree biTree; char tag; }BiTNodePost, *BiTreePost; void PostOrder(BiTree T) { stack<BiTreePost> stack; //p是遍历指针 BiTree p = T; BiTreePost BT; //栈不空或者p不空时循环 while (p != NULL || !stack.empty()) { //遍历左子树 while (p != NULL) { BT = (BiTreePost)malloc(sizeof(BiTNodePost)); BT->biTree = p; //访问过左子树 BT->tag = 'L'; stack.push(BT); p = p->lchild; } //左右子树访问完毕访问根节点 while (!stack.empty() && (stack.top())->tag == 'R') { BT = stack.top(); //退栈 stack.pop(); BT->biTree; cout<<BT->biTree->data<<" "; } //遍历右子树 if (!stack.empty()) { BT = stack.top(); //访问过右子树 BT->tag = 'R'; p = BT->biTree; p = p->rchild; } } } //层次遍历(非递归) void LevelOrder(BiTree T) { BiTree p = T; queue<BiTree> queue; //根节点入队 queue.push(p); //队列不空循环 while (!queue.empty()) { //对头元素出队 p = queue.front(); //访问p指向的结点 operation1(p->data); //退出队列 queue.pop(); //左孩子不为空,将左孩子入队 if (p->lchild != NULL) { queue.push(p->lchild); } //右孩子不空,将右孩子入队 if (p->rchild != NULL) { queue.push(p->rchild); } } } int main() { int level = 1; //表层数 BiTree T = NULL; cout << "请以先序遍历的方式输入扩展二叉树:"; //类似输入AB#D##C## CreateBiTree(&T);// 建立二叉树,没有树,怎么遍历 cout << "先序遍历输出为:" << endl; PreOrderTraverse(T, level);//进行前序遍历,其中operation1()和operation2()函数表示对遍历的结点数据进行的处理操作 cout << endl; cout << "中序遍历输出为:" << endl; InOrderTraverse(T, level); cout << endl; cout << "后序遍历输出为:" << endl; PostOrderTraverse(T, level); cout << endl; cout<<"非递归前序遍历输出为:"<<endl; PreOrder(T); cout<<endl; cout<<"非递归前序遍历输出为:"<<endl; InOrder(T); cout<<endl; cout<<"非递归前序遍历输出为:"<<endl; PostOrder(T); cout<<endl; cout<<"层序遍历输出为:"<<endl; LevelOrder(T); cout<<endl; return 0; }

实验内容二:以实验内容一所示链表为存储结构,编写程序实现求二叉树节点个数、叶子节点个数、二叉树的高度以及交换二叉树所有子树的操作
在原先代码的基础上分别加入了三个计数和交换子树的代码
count.cpp
#include<iostream> #include<stdlib.h> #include<stack> #include<queue> using namespace std; typedef char ElemType; typedef struct BiTNode { ElemType data;//数据域 struct BiTNode *lchild, *rchild;//左孩子和右孩子 }BiTNode, *BiTree; //根据试验要求,用先序创建的方式进行构建二叉树 //邹老师代课时建议我们加上层次遍历,希望李老师喜欢哈哈 void CreateBiTree(BiTree *T) { ElemType ch; cin >> ch; if (ch == '#') *T = NULL; else { *T = (BiTree)malloc(sizeof(BiTNode)); (*T)->data = ch;//生成结点 CreateBiTree(&(*T)->lchild);//构造左子树 CreateBiTree(&(*T)->rchild);//构造右子树 } } //先序遍历 void operation1(ElemType ch) { cout << ch << " "; } //此处在输出的基础上,并输出层数 void operation2(ElemType ch, int level) { cout << ch << "在第" << level << "层" << " "; } //先序遍历二叉树(递归方式) void PreOrderTraverse(BiTree T, int level) { if (T == NULL) return; operation1(T->data); //operation2(T->data, level); //可输出层数 PreOrderTraverse(T->lchild, level + 1); PreOrderTraverse(T->rchild, level + 1); } //中序遍历二叉树(递归方式) void InOrderTraverse(BiTree T,int level) { if(T==NULL) return; InOrderTraverse(T->lchild,level+1); operation1(T->data); //operation2(T->data, level); //可输出层数 InOrderTraverse(T->rchild,level+1); } //后序遍历二叉树(递归方式) void PostOrderTraverse(BiTree T,int level) { if(T==NULL) return; PostOrderTraverse(T->lchild,level+1); PostOrderTraverse(T->rchild,level+1); operation1(T->data); //operation2(T->data, level); //可输出层数 } /* 思路:将T入栈,遍历左子树;遍历完左子树返回时,栈顶元素应为T,出栈,再先序遍历T的右子树。*/ void PreOrder(BiTree T){ stack<BiTree> stack; //p是遍历指针 BiTree p = T; //p不为空或者栈不空时循环 while (p || !stack.empty()) { if (p != NULL) { //存入栈中 stack.push(p); //对树中的结点进行操作 operation1(p->data); //遍历左子树 p = p->lchild; } else { //退栈 p = stack.top(); stack.pop(); //访问右子树 p = p->rchild; } } } //中序遍历(非递归) void InOrder(BiTree T) { stack<BiTree> stack; //p是遍历指针 BiTree p = T; //p不为空或者栈不空时循环 while (p || !stack.empty()) { if (p != NULL) { //存入栈中 stack.push(p); //遍历左子树 p = p->lchild; } else { //退栈 p = stack.top(); operation1(p->data); //对树中的结点进行操作 stack.pop(); //访问右子树 p = p->rchild; } } } //后序遍历(非递归) typedef struct BiTNodePost{ BiTree biTree; char tag; }BiTNodePost, *BiTreePost; void PostOrder(BiTree T) { stack<BiTreePost> stack; //p是遍历指针 BiTree p = T; BiTreePost BT; //栈不空或者p不空时循环 while (p != NULL || !stack.empty()) { //遍历左子树 while (p != NULL) { BT = (BiTreePost)malloc(sizeof(BiTNodePost)); BT->biTree = p; //访问过左子树 BT->tag = 'L'; stack.push(BT); p = p->lchild; } //左右子树访问完毕访问根节点 while (!stack.empty() && (stack.top())->tag == 'R') { BT = stack.top(); //退栈 stack.pop(); BT->biTree; cout<<BT->biTree->data<<" "; } //遍历右子树 if (!stack.empty()) { BT = stack.top(); //访问过右子树 BT->tag = 'R'; p = BT->biTree; p = p->rchild; } } } //层次遍历(非递归) void LevelOrder(BiTree T) { BiTree p = T; queue<BiTree> queue; //根节点入队 queue.push(p); //队列不空循环 while (!queue.empty()) { //对头元素出队 p = queue.front(); //访问p指向的结点 operation1(p->data); //退出队列 queue.pop(); //左孩子不为空,将左孩子入队 if (p->lchild != NULL) { queue.push(p->lchild); } //右孩子不空,将右孩子入队 if (p->rchild != NULL) { queue.push(p->rchild); } } } //求二叉树的高度,遍历左右子树,分别计数,取最大值+1 int TreeHeight(BiTree T) { int Height=0; if(T) { int LeftHeight=TreeHeight(T->lchild); int RightHeight=TreeHeight(T->rchild); Height=LeftHeight>=RightHeight?LeftHeight+1:RightHeight+1; } return Height; } //求结点个数,遍历中计数左右子树的根节点+1 int countNode(BiTree T) { int nodenum=0; int l=0; int r=0; if(!T) return 0; if(T){ l=countNode(T->lchild); r=countNode(T->rchild); } nodenum=l+r+1; return nodenum; } //求叶子结点个数,方法:在遍历中既没有左子树又没有左子树就是叶子叶子结点 int Leafcount(BiTree T,int &num) { if(T) { if(T->lchild ==NULL &&T->rchild==NULL) num++; Leafcount(T->lchild,num); Leafcount(T->rchild,num); } return num; } //交换左右子树 void ReverseLeftRightChild(BiTNode **T) { // 如果是叶子节点,则递归结束 if (*T == NULL) { return; } swap((*T)->lchild, (*T)->rchild); // 直接使用swap交换函数比较方便,直接交换指针; ReverseLeftRightChild(&((*T)->lchild)); ReverseLeftRightChild(&((*T)->rchild)); } int main() { int num=0; int level = 1; //表层数 BiTree T = NULL; cout << "请以先序遍历的方式输入扩展二叉树:"; CreateBiTree(&T);// 建立二叉树 cout << "先序遍历输出为:" << endl; PreOrderTraverse(T, level); cout << endl; cout << "中序遍历输出为:" << endl; InOrderTraverse(T, level); cout << endl; cout << "后序遍历输出为:" << endl; PostOrderTraverse(T, level); cout << endl; cout<<"非递归前序遍历输出为:"<<endl; PreOrder(T); cout<<endl; cout<<"非递归前序遍历输出为:"<<endl; InOrder(T); cout<<endl; cout<<"非递归前序遍历输出为:"<<endl; PostOrder(T); cout<<endl; cout<<"层序遍历输出为:"<<endl; LevelOrder(T); cout<<endl; int height=TreeHeight(T); cout<<"二叉树的高度为:"<<height<<endl; int nodenum=countNode(T); cout<<"二叉树的结点个数为"<<nodenum<<endl; Leafcount(T,num); cout<<"二叉树的叶子结点个数为"<<num<<endl; ReverseLeftRightChild(&T); cout << "先序遍历输出为:" << endl; PreOrderTraverse(T, level); cout<<endl; return 0; }

实验内容三:编写程序,实现哈夫曼树的创建、哈夫曼编码以及编码的实现
哈夫曼算法:
给定N个权值,{w1,w2,w3,···,wn}
- 用给定的权值构建N个左右子树都为空的二叉树,N棵形成森林;
- 从中选取权值最小和次最小的两棵树作为左右子树,构成新的二叉树,新二叉树的权值为两棵二叉树权值之和。我们约定左子树的权值要小于右子树的权值;
- 从原权值集合中删除在上一步中使用的两棵子树,并将新子树加入集合;
- 循环执行,最后可得一棵哈夫曼树。
代码如下:
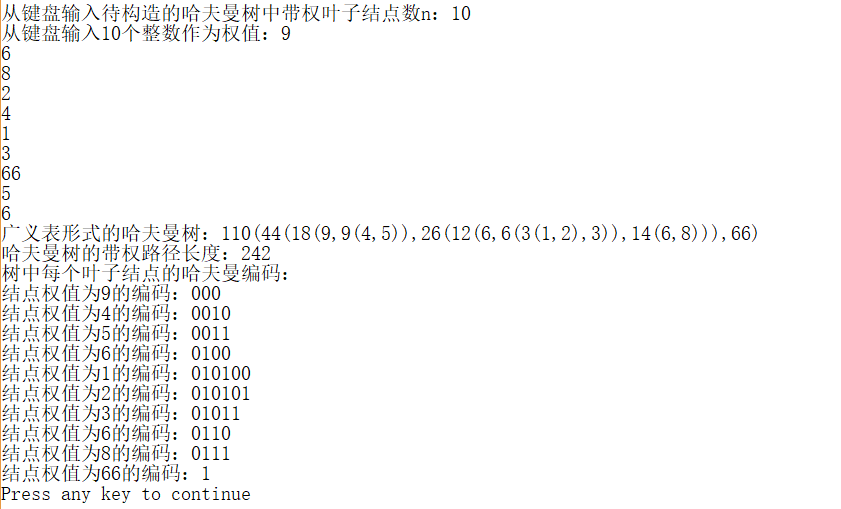
构造哈夫曼树.c
/*构造哈夫曼树的算法*/ /*哈夫曼树,又称最优树,是一类带权路径长度最短的树。 树的带权路径长度,是树中所有叶子 节点的带权路径长度之和。 通常记做WPL=W1*L1+W2*L2+...+Wn*Ln。*/ #include<stdio.h> #include<stdlib.h> typedef int ElemType; struct BTreeNode { ElemType data; struct BTreeNode* left; struct BTreeNode* right; }; //1、输出二叉树,可在前序遍历的基础上修改。采用广义表格式,元素类型为int void PrintBTree_int(struct BTreeNode* BT) { if (BT != NULL) { printf("%d", BT->data); //输出根结点的值 if (BT->left != NULL || BT->right != NULL) { printf("("); PrintBTree_int(BT->left); //输出左子树 if (BT->right != NULL) printf(","); PrintBTree_int(BT->right); //输出右子树 printf(")"); } } } //2、根据数组 a 中 n 个权值建立一棵哈夫曼树,返回树根指针 struct BTreeNode* CreateHuffman(ElemType a[], int n) { int i, j; struct BTreeNode **b, *q; b = malloc(n*sizeof(struct BTreeNode)); for (i = 0; i < n; i++) //初始化b指针数组,使每个指针元素指向a数组中对应的元素结点 { b[i] = malloc(sizeof(struct BTreeNode)); b[i]->data = a[i]; b[i]->left = b[i]->right = NULL; } for (i = 1; i < n; i++)//进行 n-1 次循环建立哈夫曼树 { //k1表示森林中具有最小权值的树根结点的下标,k2为次最小的下标 int k1 = -1, k2; for (j = 0; j < n; j++)//让k1初始指向森林中第一棵树,k2指向第二棵 { if (b[j] != NULL && k1 == -1) { k1 = j; continue; } if (b[j] != NULL) { k2 = j; break; } } for (j = k2; j < n; j++)//从当前森林中求出最小权值树和次最小 { if (b[j] != NULL) { if (b[j]->data < b[k1]->data) { k2 = k1; k1 = j; } else if (b[j]->data < b[k2]->data) k2 = j; } } //由最小权值树和次最小权值树建立一棵新树,q指向树根结点 q = malloc(sizeof(struct BTreeNode)); q->data = b[k1]->data + b[k2]->data; q->left = b[k1]; q->right = b[k2]; b[k1] = q;//将指向新树的指针赋给b指针数组中k1位置 b[k2] = NULL;//k2位置为空 } free(b); //删除动态建立的数组b return q; //返回整个哈夫曼树的树根指针 } //3、求哈夫曼树的带权路径长度 ElemType WeightPathLength(struct BTreeNode* FBT, int len)//len初始为0 { if (FBT == NULL) //空树返回0 return 0; else { if (FBT->left == NULL && FBT->right == NULL)//访问到叶子结点 return FBT->data * len; else //访问到非叶子结点,进行递归调用,返回左右子树的带权路径长度之和,len递增 return WeightPathLength(FBT->left,len+1)+WeightPathLength(FBT->right,len+1); } } //4、哈夫曼编码(可以根据哈夫曼树带权路径长度的算法基础上进行修改) void HuffManCoding(struct BTreeNode* FBT, int len)//len初始值为0 { static int a[10];//定义静态数组a,保存每个叶子的编码,数组长度至少是树深度减一 if (FBT != NULL)//访问到叶子结点时输出其保存在数组a中的0和1序列编码 { if (FBT->left == NULL && FBT->right == NULL) { int i; printf("结点权值为%d的编码:", FBT->data); for (i = 0; i < len; i++) printf("%d", a[i]); printf(" "); } else//访问到非叶子结点时分别向左右子树递归调用,并把分支上的0、1编码保存到数组a { //的对应元素中,向下深入一层时len值增1 a[len] = 0; HuffManCoding(FBT->left, len + 1); a[len] = 1; HuffManCoding(FBT->right, len + 1); } } } //主函数 void main() { int n, i; ElemType* a; struct BTreeNode* fbt; printf("从键盘输入待构造的哈夫曼树中带权叶子结点数n:"); while(1) { scanf("%d", &n); if (n > 1) break; else printf("重输n值:"); } a = malloc(n*sizeof(ElemType)); printf("从键盘输入%d个整数作为权值:", n); for (i = 0; i < n; i++) scanf(" %d", &a[i]); fbt = CreateHuffman(a, n); printf("广义表形式的哈夫曼树:"); PrintBTree_int(fbt); printf(" "); printf("哈夫曼树的带权路径长度:"); printf("%d ", WeightPathLength(fbt, 0)); printf("树中每个叶子结点的哈夫曼编码: "); HuffManCoding(fbt, 0); }