题目链接
647. 回文子串
题目描述
示例 1:
输入:"abc"
输出:3
解释:三个回文子串: "a", "b", "c"
示例 2:
输入:"aaa"
输出:6
解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
提示:
输入的字符串长度不会超过 1000 。
解题思路
1.暴力枚举
- 字符串问题最土最有效的方法应该就是暴力枚举了,利用双重for循环可以得到字符串s的所有子串,然后对这些子串进行一一判断,如果是回文串,ans++;
- 一般来说,暴力都会被卡超时,没想到这题竟然过了
2.中心扩展法
通过观察可以发现,回文字符串分为两种:
- 偶数型回文字符串:如果回文字符串的长度为偶数,那么它中间一定是两个相同的元素,例如cbaabc,中间是两个相同的aa;
- 奇数型回文字符串:如果回文字符串的长度为奇数,那么它中间一定是一个元素,例如cbabc,中间一个a元素;
所以用for先找偶数型(aa)回文,找s[i]=s[i+1],找到后再往两边推,直到s[i-len]与s[i+1+len]不等为止。
然后再找奇数型(aba)回文,找s[i]=s[i+2],找到后处理同上。
因为这是从回文中间出发,所以也叫中心扩展法。
3.动态规划
动态规划一般也只能应用于有最优子结构的问题。最优子结构的意思是局部最优解能决定全局最优解(对有些问题这个要求并不能完全满足,故有时需要引入一定的近似)。简单地说,问题能够分解成子问题来解决。
动态规划算法分以下4个步骤:
(1)描述最优解的结构
(2)递归定义最优解的值
(3)按自底向上的方式计算最优解的值 //此3步构成动态规划解的基础。
(4)由计算出的结果构造一个最优解。 //此步如果只要求计算最优解的值时,可省略。
好,接下来,咱们讨论适合采用动态规划方法的最优化问题的俩个要素:最优子结构性质,和子问题重叠性质。
(1)最优子结构
如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理)。意思就是,总问题包含很多个子问题,而这些子问题的解也是最优的。
(2)重叠子问题
子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地查看一下结果,从而获得较高的效率。
该问题满足最优子结构性质:一个最长回文串去掉两头以后,剩下的部分依然是最长回文串。
第一步:定义状态
dp[i][j]:表示子串s[i,j]是否为回文子串。
当dp[i][j] = 1:表示子串s[i,j]为回文子串,反之。
第二步:状态转移方程
这一步在做分类讨论(根据头尾字符是否相等)。
if(j-i >= 2){
dp[i][j] = 1, if dp[i+1][j-1] == 1 && s[i] == s[j]
dp[i][j] = 0, if dp[i+1][j-1] == 0 || s[i] != s[j]
}
else{
dp[i][j] = 1,if s[i] == s[j]
dp[i][j] = 0,if s[i] != s[j]
}
-Q:j-i >= 2这个条件是如何求解出来的?
-A:因为dp[i][j]表示子串s[i,j]是否为回文子串,所以i<=j,同理dp[i+1][j-1]中,i+1 <= j-1,整理得j - i <= 2.
第三步:考虑初始化
初始化的时候,单个字符一定是回文串,因此把对角线先初始化为 1,即 dp[i,i] = 1 。
第四步:考虑输出
判断dp[i,j]是否等于 1,等于的话ans++即可。
第五步:考虑状态是否可以压缩
因为在填表的过程中,只参考了左下方的数值。事实上可以压缩,但会增加一些判断语句,增加代码编写和理解的难度,丢失可读性。在这里不做状态压缩。
AC代码
1.暴力枚举
class Solution {
//判断是否为回文子串建议都这样写for循环语句,这样能够减少循环次数。
boolean charge(String s){
for(int i = 0; i < s.length() / 2; i++){
if(s.charAt(i) != s.charAt(s.length() - i - 1)) return false;
}
return true;
}
public int countSubstrings(String s) {
//因为单个字母也算回文,所以ans的初始值就是字符串的长度。
int ans = s.length();
for(int i = 0; i < s.length() - 1; i++){
StringBuilder sb = new StringBuilder();
sb.append(s.charAt(i));
for(int j = i + 1; j < s.length(); j++){
sb.append(s.charAt(j));
if(charge(sb.toString())){
ans++;
}
}
}
return ans;
}
}
2.中心扩展法
class Solution {
public int countSubstrings(String s) {
int ans = s.length();
//奇数型回文
for(int i = 0; i < s.length() - 2; i++){
if(s.charAt(i) == s.charAt(i+2)){
ans++;
int temp = 1;
while((i-temp)>=0 && (i+2+temp)<s.length() && s.charAt(i-temp)==s.charAt(i+2+temp)){
ans++;
temp++;
}
}
}
//偶数型回文
for(int i = 0; i < s.length() - 1; i++){
if(s.charAt(i) == s.charAt(i+1)){
ans++;
int temp = 1;
while((i-temp)>=0&&(i+1+temp)<s.length() && s.charAt(i-temp)==s.charAt(i+1+temp)){
ans++;
temp++;
}
}
}
return ans;
}
}
3.动态规划法
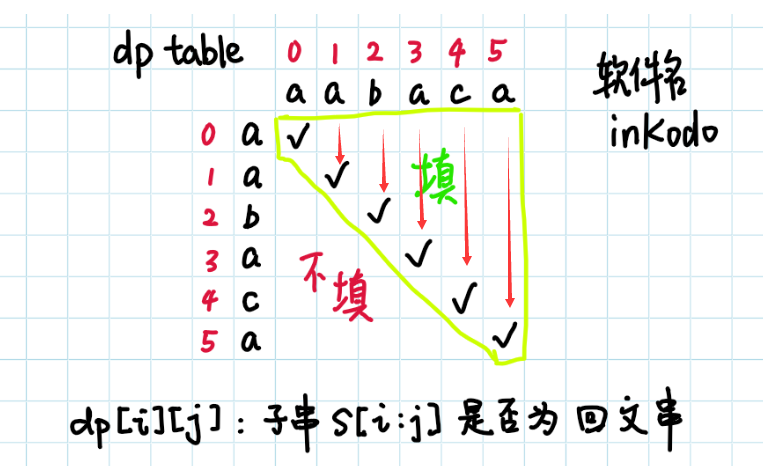
填表必须是从上往下如箭头所示,一开始我选择从左到右填表,卡了很久。
dp[0][5]依赖与dp[1][4]以及s[0]s[5]是否相等,如果你是从左到右填表,那dp[1][4]的值是未知的。
class Solution {
public int countSubstrings(String s) {
int[][] dp = new int[s.length()][s.length()];
int ans = 0;
for(int i = 0; i < s.length(); i++){
dp[i][i] = 1;
ans++;
}
//下面的两个for循环就是在填表格!但是要注意填表的顺序!!!!!!!!
for(int j = 0; j < s.length(); j++){
for(int i = 0; i < j; i++){
if(j - i <= 2){
if(s.charAt(j) == s.charAt(i)) dp[i][j] = 1;
else dp[i][j] = 0;
}
else{
if(s.charAt(j) == s.charAt(i) && dp[i+1][j-1]==1) dp[i][j] = 1;
else dp[i][j] = 0;
}
if(dp[i][j] == 1) ans++;
}
}
return ans;
}
}