【LeetCode】51.N皇后(回溯)

题目链接

51. N 皇后

题目描述

解题思路

1.经典回溯

普通八皇后问题只需要求出有多少种可行方案即可，而本题稍微更难一点，还需要把这些可行方案记录并打印。

之前也说到遇到递归问题，两件分析法宝：画出递归树以及函数栈！本题递归树如下:

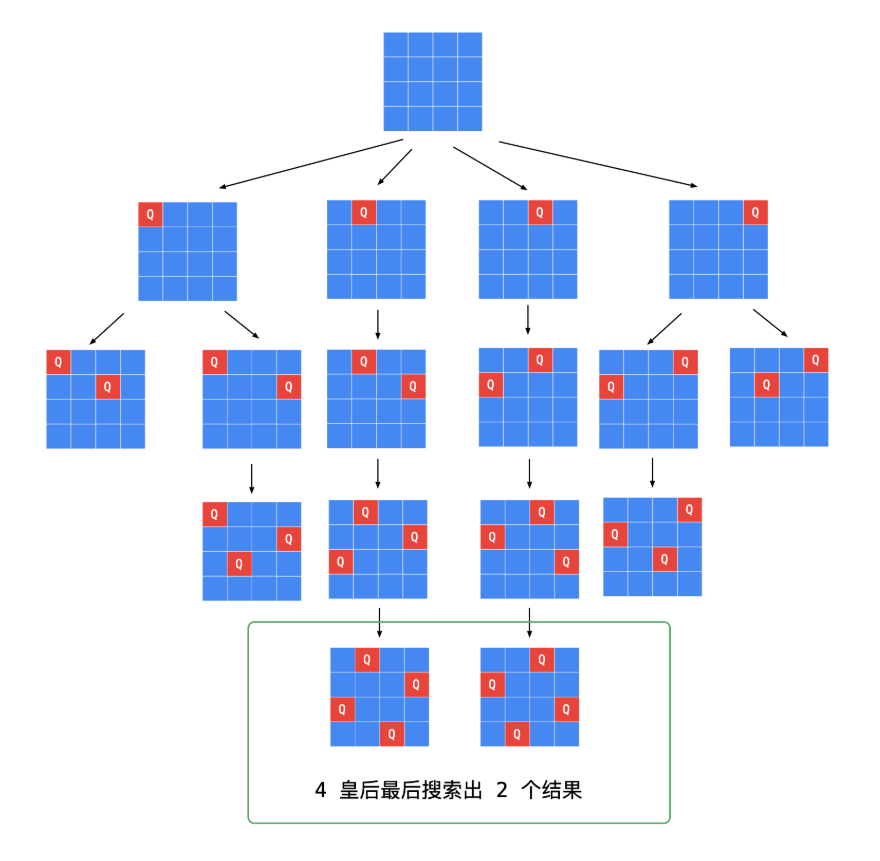
遇到的问题如下

（1）回溯过程中递归返回条件的判断：如何判断两个皇后是否在一条斜线上？

一开始打算利用max(x,y)/min(x,y)进行判断，但是由于都是整数除法，存在一些情况是行不通的，遂放弃。

观察之后，可以发现有以下规律：

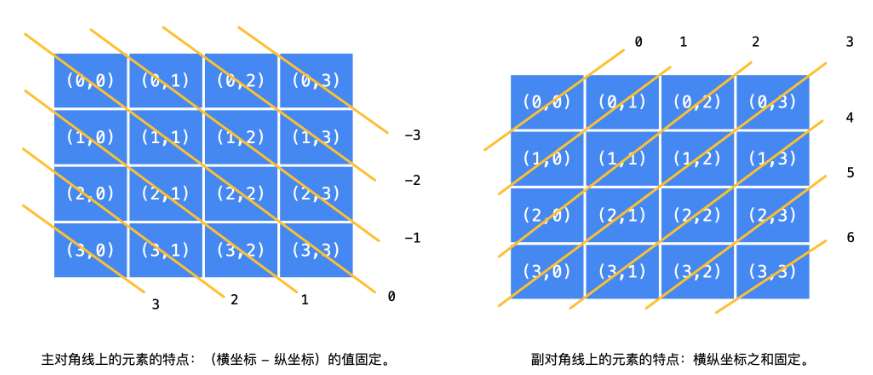
利用两个一维数组分别表示主对角线和副对角线。

//主对角线，当n=4的时候，一共有7个值，也就是2*n-1个值，因为数组索引必须大于等于0，所以当(x-y)<0的时候，还需要+2*n-1;
int main_dia[] = new int[2*n-1];
int counter_dia[] = new int[2*n-1];

（2）回溯代码的细节问题。

AC代码中，赋值为1的代码必须和for循环结束赋值为0的代码的位置是对称的，也就是要么两个都在for循环内，要么两个代码段都在for循环外，不能一里一外

AC代码

class Solution {    
    List<List<String>> ans = new ArrayList<>();
    void dfs(int x,int y,int[] x_valid,int[] y_valid,int[] main_dia,int[] counter_dia,int n,int board[][]){
        if(x == n) return;
        if(x_valid[x]==1) return;
        if(y_valid[y]==1) return;
        if(main_dia[x+y]==1) return;
        if(x-y<0&&counter_dia[x-y+2*n-1]==1) return;
        if(x-y>=0&&counter_dia[x-y]==1) return;
        if(x == n -1){
            List<String> temp = new ArrayList<>();
            board[x][y]=1;
            for(int i = 0; i < n; i++){
                StringBuffer sb = new StringBuffer();
                for(int j = 0; j < n; j++){
                    if(board[i][j]==1) sb.append("Q");
                    else sb.append(".");
                }
                temp.add(sb.toString());
            }
            ans.add(temp);
        }
        //这段赋值为1的代码必须和for循环结束赋值为0的代码的位置是对称的，也就是要么两个都在for循环内，要么两个代码段都在for循环外，不能一里一外
        x_valid[x]=1;
        y_valid[y]=1;
        main_dia[x+y]=1;
        board[x][y]=1;
        if(x-y<0) counter_dia[x-y+2*n-1] = 1;
        else counter_dia[x-y]=1;
        for(int i = 0; i < n; i++){
            dfs(x+1,i,x_valid,y_valid,main_dia,counter_dia,n,board);
        } 
        x_valid[x]=0;
        y_valid[y]=0;
        board[x][y]=0;
        main_dia[x+y]=0;
        if(x-y<0) counter_dia[x-y+2*n-1] = 0;
        else counter_dia[x-y]=0;
    }

    public List<List<String>> solveNQueens(int n) {
        int x_valid[] = new int[n];
        int y_valid[] = new int[n];
        int main_dia[] = new int[2*n-1];
        int counter_dia[] = new int[2*n-1];
        int board[][] = new int[n][n];
        for(int i = 0; i < n; i++){
            dfs(0,i,x_valid,y_valid,main_dia,counter_dia,n,board);
        }
        return ans;
    }
}