前言
小时候家里大人不让玩手机,所以我常玩的是华容道益智游戏,一关就要解很久,解不开也没心思去做别的事了。如果用算法解决实际生活中的问题,那么我第一个想解决的是快速通关华容道。
华容道是在一个拼图中有一个格子是空的,利用这个空着的格子去移动其他的滑块(卒、张飞、赵云、关羽等),最后顺利让曹操从中间的空格出来。以第二关七步成诗进行操作,最初,没有用考虑最少步数完成,如图:
这种游戏一般都有一些套路,类似于魔方还原公式,使用的是一些技巧,我们不研究这个令人脑壳痛的技巧,学了算法后知道这个可以使用快乐无比的暴力搜索算法解决————BFS算法框架解决类似的益智游戏。
BFS算法框架
BFS核心思想是把一些问题抽象成图,从一个点开始,像四周扩散,找到到终点最近的距离。常使用的是队列这个数据结构,每次将一个节点周围的所有节点加入队列。
BFS算法框架
//计算从起点到终点最近距离
int BFS(Node start,Node target){
Queue<Node> q;//队列q,核心数据结构
Set<Node> visited;//避免走回头路
q.offer(start);//将起点加入队列
visited.add(start);
int step=0;//记录扩散的步数
while(q not empty){
int sz=q.size();
/*将当前队列所有的节点像四周扩散*/
for(int i=0;i<sz;i++){
Node cur =q.poll();
/*划重点:这里判断是否到达终点*/
if(cur is target)
return step;
/*将cur的相邻界点加入队列*/
for(Node x:cur.adj()){
if(x not in visited){
q.offer(x);
visited.add(x);
}
}
/*划重点:更新步数*/
step++;
}
}
cur.adj()泛指cur相邻的节点,比如说二维数组中,cur上下左右四面的位置,就是相邻的节点。
visited的主要作用是防止走回头路。
BFS与DFS
DFS用递归的形式,用到了栈结构,先进后出。
BFS选取状态用队列的形式,先进先出。
DFS的复杂度与BFS的复杂度大体一致,不同之处在于遍历的方式与对于问题的解决出发点不同。
一般来说哈,在找最短路径的时候使用BFS,其他时候DFS偏多,主要是递归代码好写叭。
双向BFS优化
传统的BFS框架是从起点开始向四周扩散,遇到终点时停止。而双向BFS则是从起点和终点同时开始扩散,当两边有交集的时候停止。双向BFS还是遵循BFS算法框架的,只是不再使用队列,而是使用HashSet方便快捷判断两个集合是否有交集。while循环的最后交换q1和q2的内容,所以只要默认扩散q1就相对轮流扩散q1和q2。
不过双向BFS也有局限性,必须得先知道终点在哪里。
问题分析
可以将其类比为滑动拼图问题,leetcode第773题滑动谜题就是滑动拼图问题,以此题为例,进行演算分析。
题目描述如下:
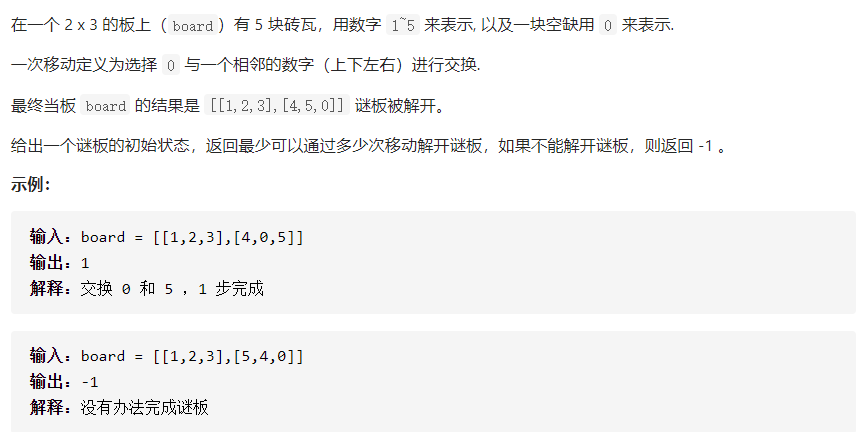

思路描述
这是计算最小步数的问题,正如之前所说,遇到这类问题,最先思考BFS算法。而这个题目转化为BFS的时候,我们会面临这样的问题:
- 一般的BFS算法时从一个起点到终点进行寻路的,拼图问题是在不断的交换数字。
- 假设这个问题可以转化为BFS问题,那么起点与终点该如何处理?把数组放入队列是个麻烦低效的事情。
BFS是一种暴力搜索算法
解决第一个问题:只要涉及暴力穷举的问题,BFS就可以用,并且可以最快的找到最优解。可以将第一个问题转化为“怎么样穷举board当前局面下可能衍生出的所有局面?”可以以数字0为基准,将0和上下左右的数字进行交换就可以了:
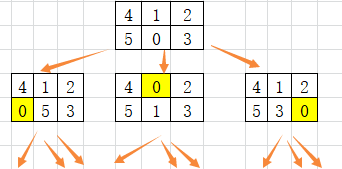
每次先找到数字0,然后和周围数字进行交换,形成新的局面加入队列,当第一次抵达终点时,就以最少步数赢得游戏。
解决第二个问题:这是一个2x3的二维数组,可以压缩为一个一维的字符串。而二维数组有上下左右的概念,压缩为一维后,获得上下左右的索引成为了一个难点。可以手动写出来这个映射,如下:
vector<vector<int>> neighbor={
{1,3},
{0,4,2},
{1,5},
{0,4},
{3,1,5},
{4,2}
};
这个含义是在一维字符串中,索引i在二维数组中的相邻索引为neighbor[i]:

eg. negihbor[4]={3,1,5}
这两个问题解决后,就可以套用之前讲到的BFS算法框架(套路):
int slidingPuzzle(vector<vector<int>>& board) {
int m = 2, n = 3;
string start = "";
string target = "123450";
// 将 2x3 的数组转化成字符串
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
start.push_back(board[i][j] + '0');
}
}
// 记录一维字符串的相邻索引
vector<vector<int>> neighbor = {
{ 1, 3 },
{ 0, 4, 2 },
{ 1, 5 },
{ 0, 4 },
{ 3, 1, 5 },
{ 4, 2 }
};
/******* BFS 算法框架开始 *******/
queue<string> q;
unordered_set<string> visited;
q.push(start);
visited.insert(start);
int step = 0;
while (!q.empty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
string cur = q.front(); q.pop();
// 判断是否达到目标局面
if (target == cur) {
return step;
}
// 找到数字 0 的索引
int idx = 0;
for (; cur[idx] != '0'; idx++);
// 将数字 0 和相邻的数字交换位置
for (int adj : neighbor[idx]) {
string new_board = cur;
swap(new_board[adj], new_board[idx]);
// 防止走回头路
if (!visited.count(new_board)) {
q.push(new_board);
visited.insert(new_board);
}
}
}
step++;
}
return -1;
/******* BFS 算法框架结束 *******/
}
结果
回到我们最初想要实现最少步数完成第二关,利用我们上面所讨论的BFS算法思想,在实际应用(微信小程序——经典三国华容道)上实践后得到七步完成第二关——七步成诗。如图:

再以实际应用(应用市场————数字华容道快应用)进行测试,未使用算法和使用算法对比后,可见明显差别,如图所示:

备注
文章书写时结合了labuladong博主有关BFS的算法描述,在问题问分析和思路描述是看了许多博客资料,自己理解后的想法。实践结果可能存在一定误差,这是因为数字华容道的每次测试,开局所给的拼图是随机的,可能存在细微的差距。