AVL树&红黑树

在认识AVL树和红黑树之前，不妨来回顾一下二叉搜索树。

二叉搜索树 Binary Search Tree

二叉搜索树，也称有序二叉树、排序二叉树，是指一颗空树或者具有下列性质的二叉树：

1. 左子树上所有结点的值均小于它的根结点的值；
2. 右子树上所有结点的值均大于它的根结点的值；
3. 以此类推：左、右子树也分别为二叉搜索树（重复性）

且二叉搜索树的中序遍历是升序排列。

二叉搜索树在极端的情况下，会退化成一个链表。

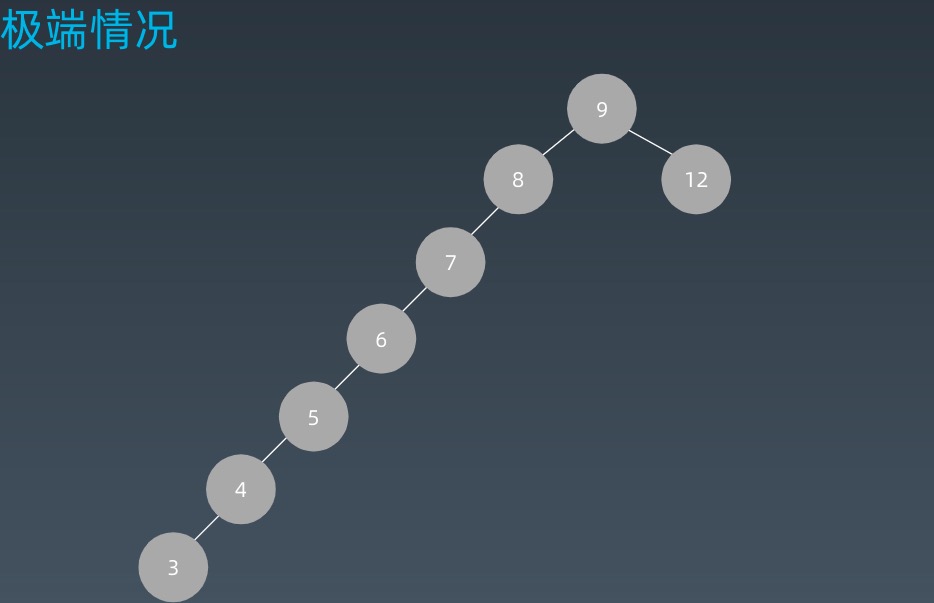
这样的话查询的时间复杂度就变成了O(n)了。

我们知道二叉搜索树的查询效率只与树的高度有关，所以要保证效率，就得想办法让二叉搜索树的左右子树高度尽可能地平衡。

这时候就引入了另外一种数据结构：平衡搜索二叉树，而AVL树和红黑树就是平衡搜索二叉树的一种。

AVL树

AVL树，是一种自平衡的树，要求左右子树的高度绝对值不能大于1。它也具备二叉搜索树的特征。

在AVL树中，有一个重要的概念

• Balance Factor（平衡因子）：左右子树高度差的绝对值。

AVL树是通过旋转操作来进行平衡（四种）

1.左旋

右右子树 -> 左旋

 

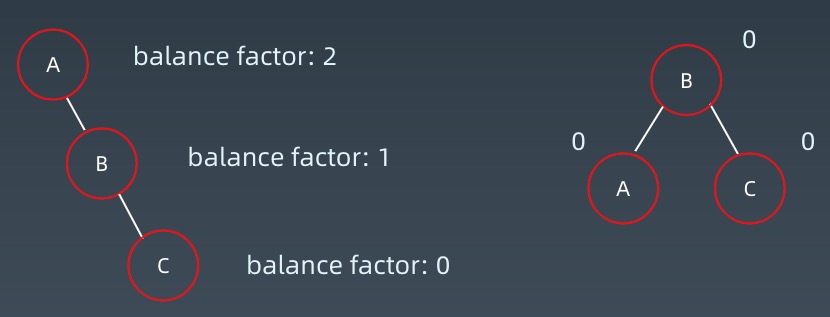
2.右旋

左左子树 -> 右旋

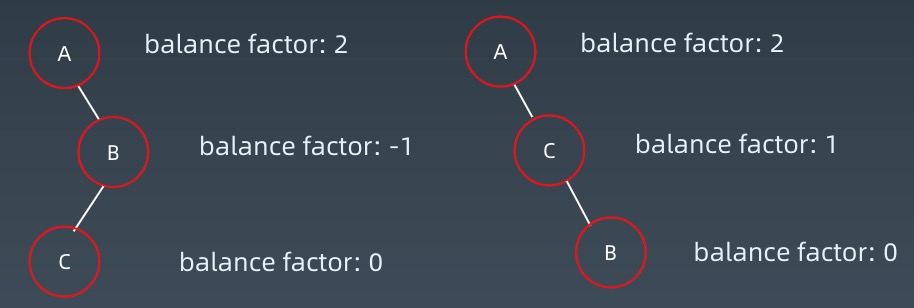
3.左右旋

左右子树 -> 左右旋

 

4.右左旋

右左子树 -> 右左旋

AVL树总结

1. 是一棵平衡二叉树
2. 每个节点都要存balance factor
3. 四种旋转操作

不足：节点需要存储额外的信息，且因为balance factor控制得比较严格，所以调整次数会比较频繁。

Red-black Tree

红黑树是一种近似平衡的二叉搜索树，它能确保任何一个结点的左右子树的高度差小于两倍。具体来说，红黑树是满足如下条件的二叉搜索树：

• 每个节点要么是红色，要么是黑色
• 根节点是黑色
• 每个叶子节点都是黑色的
• 不能有相邻的两个红色节点
• 从任一节点到其每个叶子节点所有的路径都包含相同数目的黑色节点

关键性质：

• 任一结点的左、右子树高度差小于2倍

AVL树和红黑树的区别

• AVL树比红黑树提供更快的查找，因为AVL树的平衡因子控制更加严格。
• 红黑树比AVL树提供更快的插入和移除操作，因为相对宽松的左右子树高度差导致旋转的次数较少。
• AVL树每个节点都要额外存储平衡因子，所以AVL树消耗的内存比较多。
• 红黑数一般是被编程语言所使用，而AVL数常用于数据库中。