PCA是用来给多维数据降维,分析提取主成分的一种算法;
优点:降低数据的复杂性,识别最重要的多个特征。
缺点:不一定需要,且可能损失有用信息。
适用数据类型:数值型数据。
怎么实现的呢?首先说明,在已标注和未标注的数据上都有降维技术,PCA是一种在对未标注数据的降维技术。
在PCA中,数据从原来的坐标系转换到了新的坐标系,新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向,第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复,重复次数为原始数据中特征的数目。我们会发现,大部分方差都包含在最前面的几个新坐标轴中。因此,我们可以忽略余下的坐标轴,即对数据进行了降维处理。
注:方差是对一维数据的特征描述;如果对多维数据或矩阵特征的分布描述需要用到协方差,协方差的数学意义在下面。
特征值分析是线性代数中的一个领域,它能够通过数据的一般格式来揭示数据的“真实”结构,即我们常说的特征向量和特征值。在等式Av = λv中,v 是特征向量, λ是特征值。特征值都是简单的标量值,因此Av = λv代表的是:如果特征向量v被某个矩阵A左乘,那么它就等于某个标量λ乘以v。幸运的是,NumPy中有寻找特征向量和特征值的模块linalg,它有eig()方法,该方法用于求解特征向量和特征值。
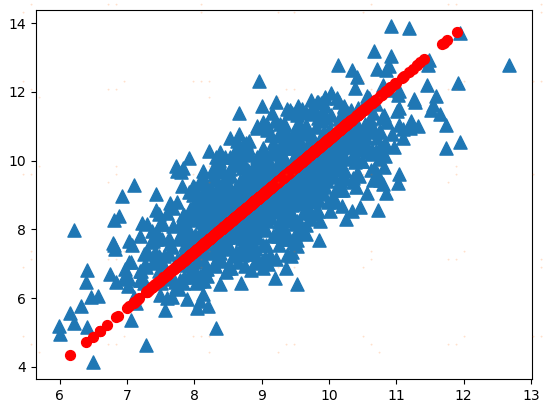
#PCA主成分分析 降维方法 #本例子展示的是用PCA处理一个590和特征的数据集,将此数据集降到6个特征 ''' 在PCA中,数据从原来的坐标系转换到新的坐标系,新坐标系的选择是由数据本身决定的。 第一个新坐标轴选择的是原始数据中方差最大的方向,第二新坐标轴的选择和第一坐标轴正交且 具有最大方差的方向。该过程一直重复,重复次数为原始数据中特征的数目。我们会发现,大部分 方差都包含在最前面的几个新坐标轴中。因此我们可以忽略余下的坐标轴,即对数据进行了降维处理。 ''' from numpy import * import matplotlib import matplotlib.pyplot as plt def loadDataSet(fileName, delim=' '): fr=open(fileName) stringArr = [line.strip().split(delim) for line in fr.readlines()] datArr = [list(map(float, line)) for line in stringArr] return mat(datArr) def pca(dataMat, topNfeat=9999999): meanVals = mean(dataMat, axis=0) meanRemoved = dataMat-meanVals #去平均值 covMat = cov(meanRemoved, rowvar=0) #计算斜方差矩阵 eigVals,eigVects = linalg.eig(mat(covMat)) #求解特征向量和特征值 eigValInd = argsort(eigVals) #从小到大对N个特征值排序 eigValInd = eigValInd[:-(topNfeat+1):-1] #删除不需要的维度 redEigVects = eigVects[:,eigValInd] lowDDataMat = meanRemoved * redEigVects #将数据转换到新空间 reconMat = (lowDDataMat * redEigVects.T) + meanVals return lowDDataMat,reconMat if __name__ == '__main__': dataMat=loadDataSet('testSet.txt') lowDMat, reconMat = pca(dataMat,1) print (shape(lowDMat)) fig=plt.figure() ax=fig.add_subplot(111) ax.scatter(dataMat[:,0].flatten().A[0],dataMat[:,1].flatten().A[0],marker='^',s=90) ax.scatter(reconMat[:,0].flatten().A[0],reconMat[:,1].flatten().A[0],marker='o',s=50, c='red') plt.show()