20172314 2018-2019-1《程序设计与数据结构》查找与排序实验报告

课程：《程序设计与数据结构》

班级： 1723

姓名： 方艺雯

学号：20172314

实验教师：王志强

实验日期：2018年12月3日

必修/选修： 必修

1、实验内容及要求

• 实验查找与排序-1

  定义一个Searching和Sorting类，并在类中实现linearSearch（教材P162 ）,SelectionSort方法（P169），最后完成测试。
  要求不少于10个测试用例，提交测试用例设计情况（正常，异常，边界，正序，逆序），用例数据中要包含自己学号的后四位
  提交运行结果图。

• 实验查找与排序-2

  重构你的代码
  把Sorting.java Searching.java放入 cn.edu.besti.cs1723.（姓名首字母+四位学号） 包中（例如：cn.edu.besti.cs1723.G2301）
  把测试代码放test包中
  重新编译，运行代码，提交编译，运行的截图（IDEA，命令行两种）

• 查找与排序-3

  参考http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching中补充查找算法并测试
  提交运行结果截图

• 查找与排序-4

  补充实现课上讲过的排序方法：希尔排序，堆排序，二叉树排序等(至少3个)
  测试实现的算法（正常，异常，边界）
  提交运行结果截图
  （3分，如果编写多个排序算法，即使其中三个排序程序有瑕疵，也可以酌情得满分）

• 查找与排序-5

  编写Android程序对各种查找与排序算法进行测试
  提交运行结果截图
  推送代码到码云

实验过程及结果

实验3-1

• 本实验只需要把以前实现过的Sorting和Searching方法运行一下，并用Junit测试正常，异常，边界，正序，逆序是否正确即可。这个实验开始一直搞不清楚异常和边界是如何判定的，那种算异常情况，最后询问同学之后解决了。异常测试是查找数组中没有的目标，所以Junit测试不通过；边界测试是查找数组中是否有边界的元素存在，若Junit测试通过，则边界测试通过。
• 实验结果
  
  
  
  
  
  
  

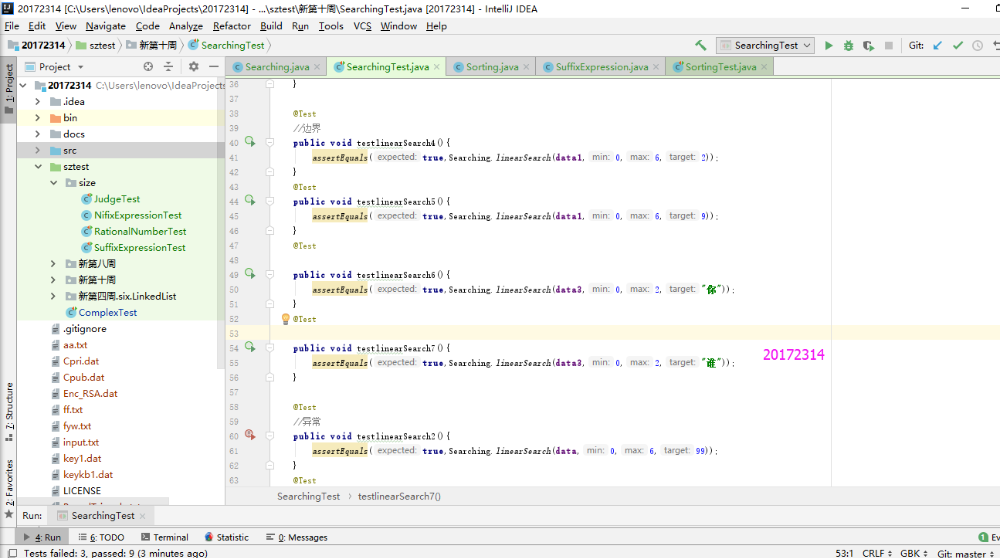
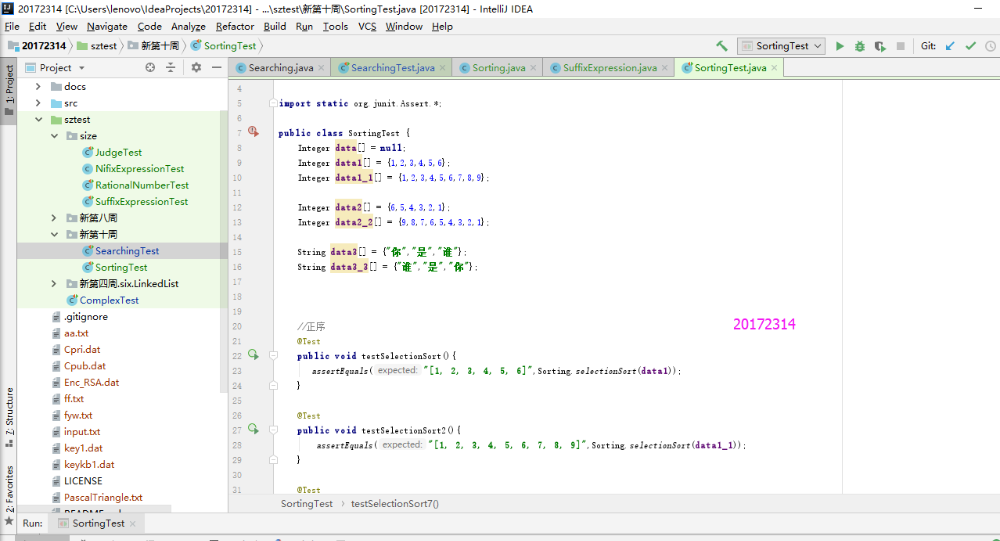
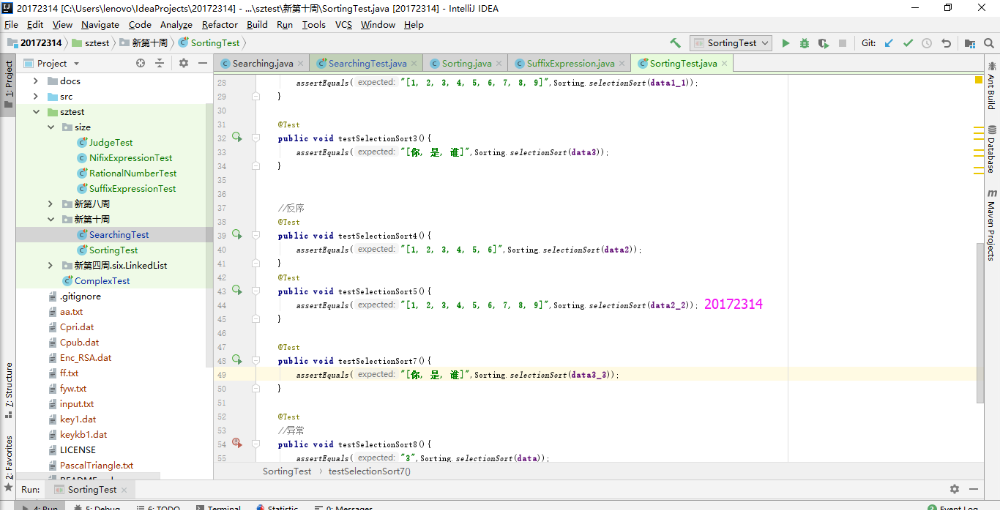
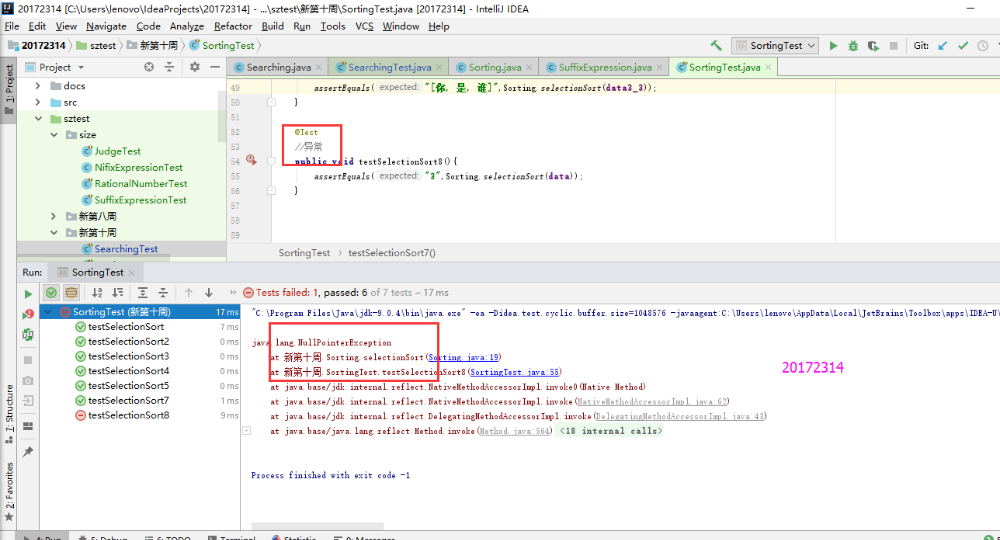
实验3-2

• 本实验只需要运行一下Sorting和Searching程序就行。由于虚拟机不能用了，需要重新下，老师说用idea也可以，所以只有idea的测试。
• 实验结果
  
  
  
  

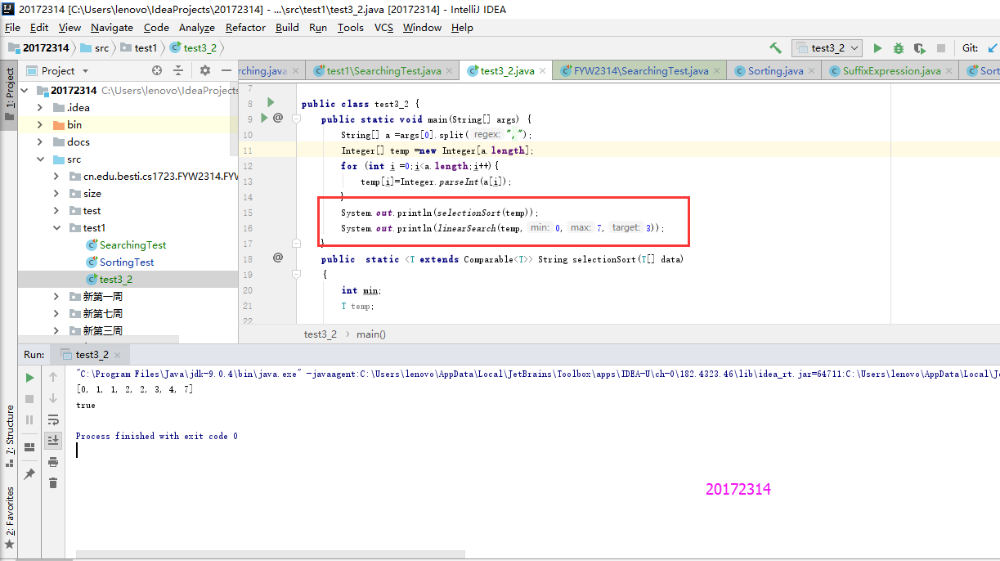
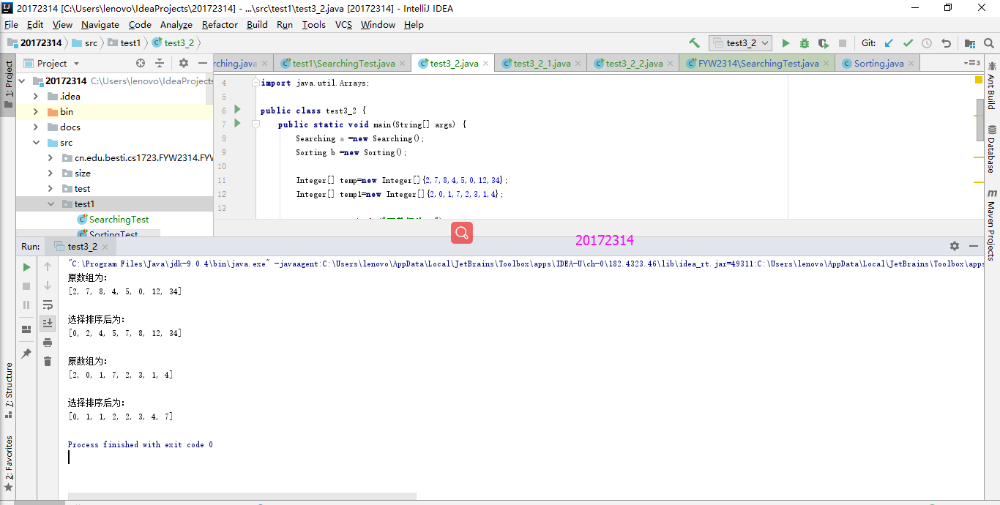
实验3-3

• 在提供的网站中有现成的部分查找算法，也有其他算法的精细讲解，然后按照提供思路实现。主要的问题是斐波那契法，之前没有学习过，在查找了相关解释后，理解为：斐波那契法与折半查找法的思路基本一致，但是区别在于斐波那契法需要构建一个数列提供分割点，其分割点的最初设置是mid = low + F[k-1] -1，原因是“斐波那契数列的后一项是前两项之和，这两项对应查找表的左右两部分，这时分割点的方式，还有一个问题就是查找表的长度是F（K）-1,原因是为了格式上的统一，以方便递归或者循环程序的编写。表中的数据是F(k)-1个，使用mid值进行分割又用掉一个，那么剩下F(k)-2个。正好分给两个子序列，每个子序列的个数分别是F(k-1)-1与F(k-2)-1个，格式上与之前是统一的。不然的话，每个子序列的元素个数有可能是F(k-1)，F(k-1)-1，F(k-2)，F(k-2)-1个，写程序会非常麻烦。”

• 新增的算法，以下是在网上查找到的详细解释：

  • 斐波那契查找与折半查找很相似，他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1，及n=F(k)-1;开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种：

    • 相等，mid位置的元素即为所求
    • 大于，low=mid+1,k-=2; （low=mid+1说明待查找的元素在[mid+1,high]范围内，k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个，所以可以递归的应用斐波那契查找。）
    • 小于，high=mid-1,k-=1。（low=mid+1说明待查找的元素在[low,mid-1]范围内，k-=1说明范围[low,mid-1]内的元素个数为F(k-1)-1个，所以可以递归 的应用斐波那契查找。

  • 复杂度分析：最坏情况下，时间复杂度为O(log2n)，且其期望复杂度也为O(log2n)。）

  • 代码

   /*定义斐波那契查找法*/
  public static int FibonacciSearch(int[] a, int n, int key)
  {
      int low = 0;
      int high = n - 1;
      //定义一个斐波那契数组
      int max = 20;
      int[] F = new int[max];
      F[0] = 1;
      F[1] = 1;
      for (int i = 2; i < max; i++) {
          F[i] = F[i - 1] + F[i - 2];
      }
      int k = 0;
      while (n > F[k] - 1)//计算n位于斐波那契数列的位置
          k++;
      int[] temp;//将数组a扩展到F[k]-1的长度
      temp = new int[F[k] - 1];
      for (int x = 0; x < a.length; x++) {
          temp[x] = a[x];
      }
      for (int i = n; i < F[k] - 1; ++i)
          temp[i] = a[n - 1];
      while (low <= high) {
          int mid = low + F[k - 1] - 1;
          if (key < temp[mid]) {
              high = mid - 1;
              k -= 1;
          } else if (key > temp[mid]) {
              low = mid + 1;
              k -= 2;
          } else {
              if (mid < n)
                  return mid; //若相等则说明mid即为查找到的位置
              else
                  return n - 1; //若mid>=n则说明是扩展的数值,返回n-1
          }
      }
      return -1;
  }
  

• 实验结果
  
  

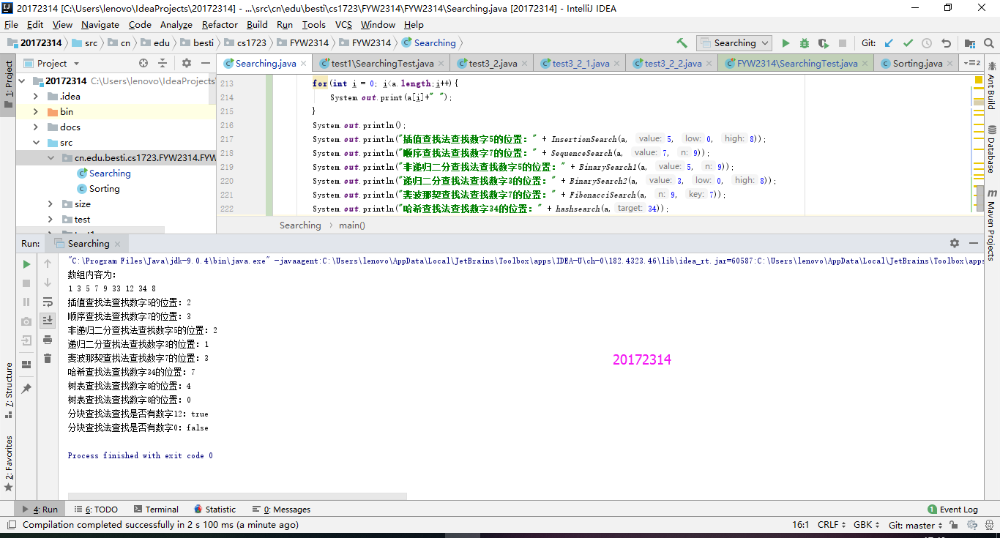
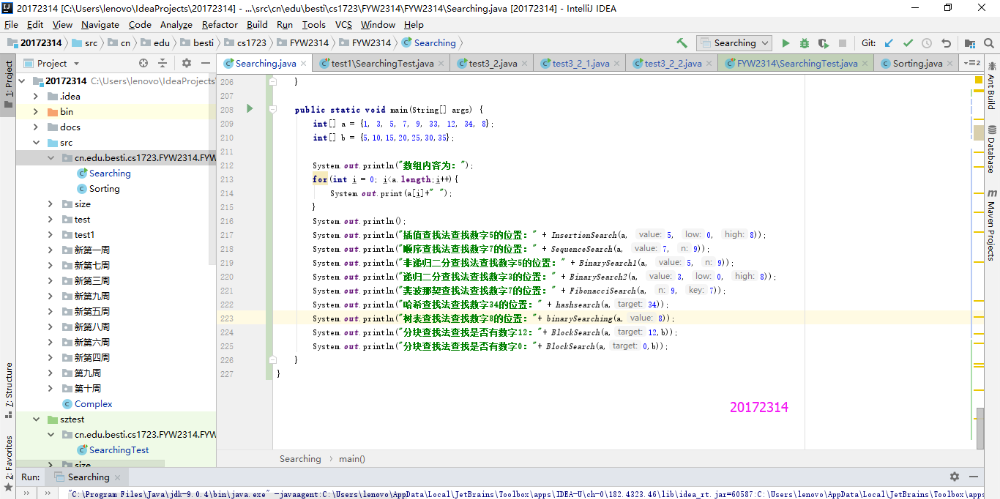
实验3-4

• 实现希尔排序，堆排序，二叉树排序，然后编写测试类测试正常，异常，边界，希尔排序和堆排序有写博客分析过，而二叉树排序是以前没有学习过的，但也较好理解。

• 希尔排序基本思想：假设序列中有n个元素，首先选择一个间隔gap，将全部的序列分为gap个子序列，然后分别在子序列内部进行简单插入排序，得到一个新的主序列；而后缩小gap，再得到子序列，对子序列进行简单插入排序，又再次得到新的主序列，直到gap=1为止。在算法中，排序前期，由于gap值比较大，插入排序的元素个数少，排序快，到了排序后期，由于前面的排序导致序列已经基本有序，插入排序对于有序的序列效率很高。

//希尔排序
    public static <T extends Comparable<T>> void shellSort(T[] data) {
        if (data == null || data.length <= 1) {
            return;
        }
        int gap = data.length / 2;
        while (gap >= 1) {
            for (int a = 0; a < data.length; a++) {
                for (int b = a; b < data.length - gap; b = b + gap) {
                    if (data[b].compareTo(data[b + gap]) > 0) {
                        T temple = data[b];
                        data[b] = data[b + gap];
                        data[b + gap] = temple;
                    }
                }
            }
            gap = gap / 2;
        }
        String result = "";
        for (int i = 0; i < data.length; i++) {
            result += data[i] + " ";
        }
        System.out.println(result);
    }

• 堆排序基本思想：把待排序的元素按照大小在二叉树位置上排列，排序好的元素要满足：父节点的元素要大于等于其子节点；这个过程叫做堆化过程，如果根节点存放的是最大的数，则叫做大根堆；如果是最小的数，自然就叫做小根堆了。根据这个特性（大根堆根最大，小根堆根最小），就可以把根节点拿出来，然后再堆化下，再把根节点拿出来，，，，循环到最后一个节点，就排序好了。整个排序主要核心就是堆化过程，堆化过程一般是用父节点和他的孩子节点进行比较，取最大的孩子节点和其进行交换；但是要注意这应该是个逆序的，先排序好子树的顺序，然后再一步步往上，到排序根节点上。然后又相反（因为根节点也可能是很小的）的，从根节点往子树上排序。最后才能把所有元素排序好。

 //堆排序
    public static <T extends Comparable<T>> void heapSort(T[] data) {
        ArrayHeap<T> temp = new ArrayHeap<T>();
        for (int i = 0; i < data.length; i++)
            temp.addElement(data[i]);
        int num = 0;
        while (!(temp.isEmpty())) {
            data[num] = temp.removeMin();
            num++;
        }
    }

• 二叉树排序基本思想：使用第一个元素作为根节点，如果之后的元素比第一个小，则放到左子树，否则放到右子树，之后按中序遍历。

    //二叉树排序
    public static <T extends Comparable<T>> void binarytreeSort(T[] data) {
        AVLTree tree = new AVLTree();
        for (int i = 0; i < data.length; i++) {
            tree.addElement(data[i]);
        }
        tree.printTree2();
    }

• 实验结果
  
  
  
  
  

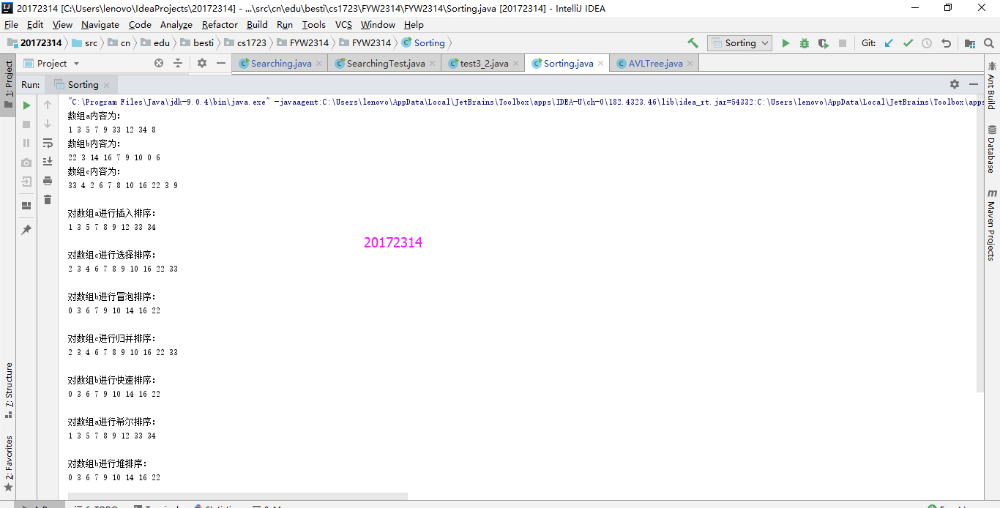
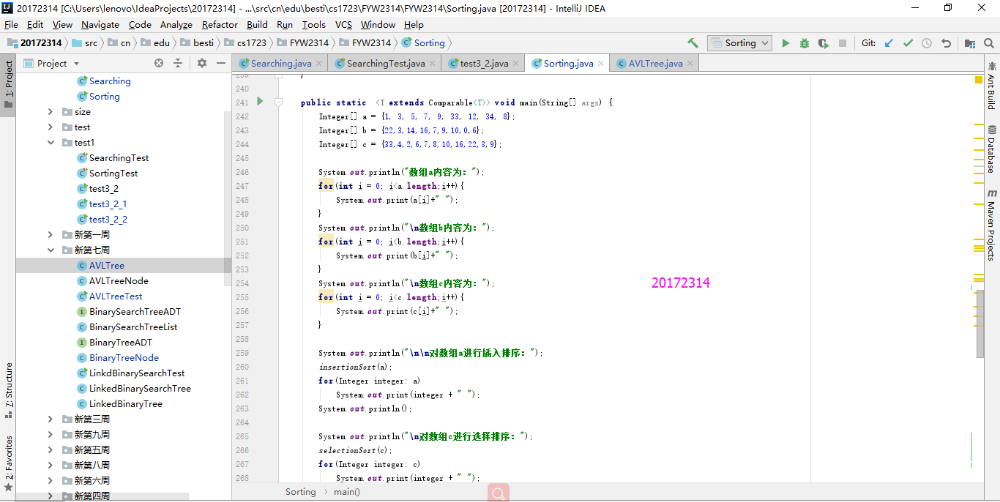
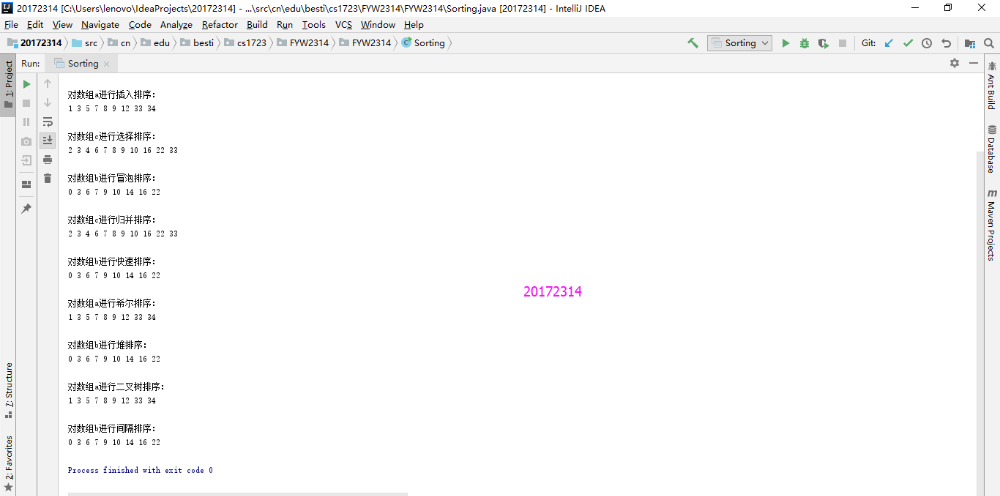
实验3-5

• 由于这两个算法牵扯到好多类，差不多移到AS上几十个类，然后对方法进行测试，添加查找和排序两个按钮，并有一个显示框显示用不同方法的结果。
• 实验结果
  
  
  
  
  

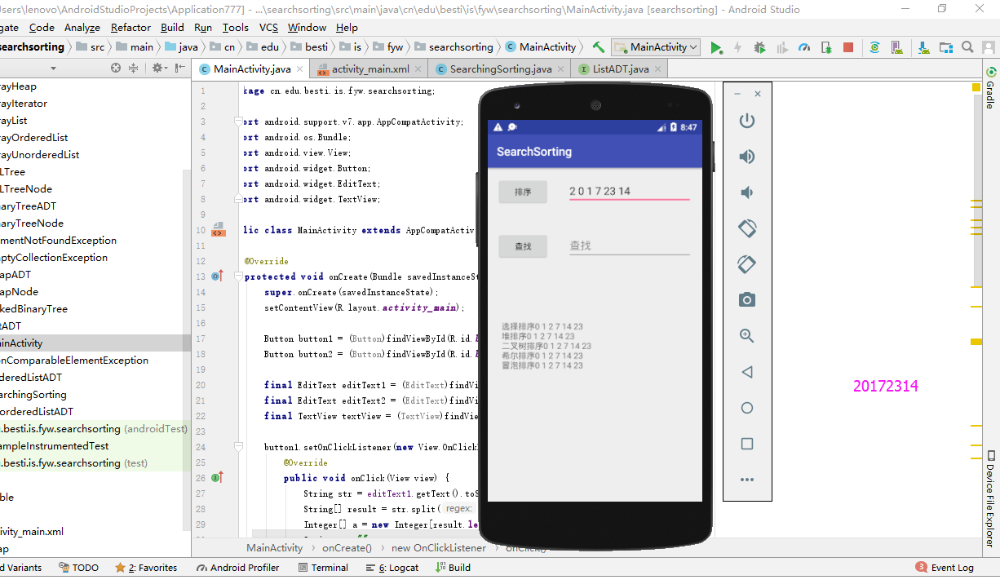
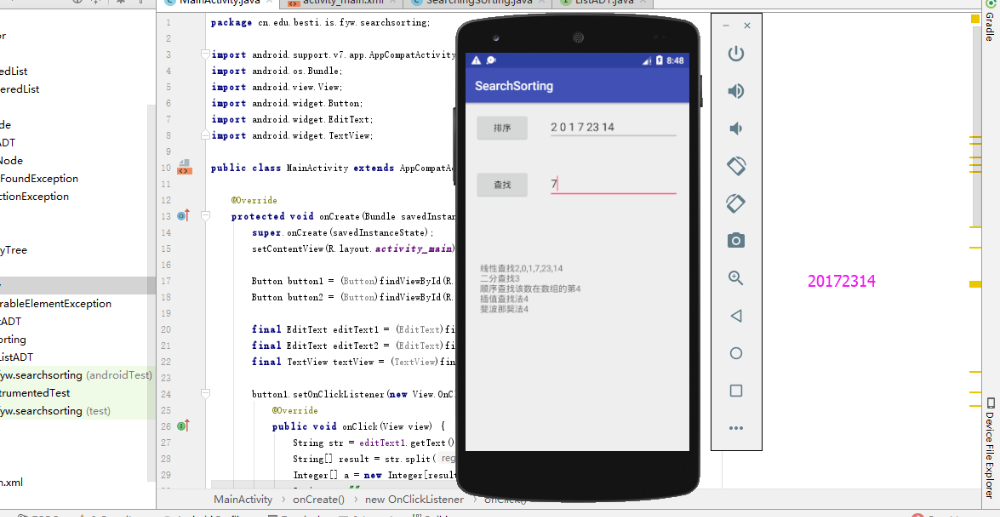
遇到的问题及解决

• 问题一：在编写测试类时，测试用的数组定义int型的就显示：需要Integer类型，找到int类型。

• 问题一解决：我本来以为这两种类型是差不多的，虽然一直不知道这两个的具体区别然后上网查找了二者区别，参考彻底让你明白 Integer 类和 int 基本数据类型的区别,其基本API为：
  
  
  
  
  

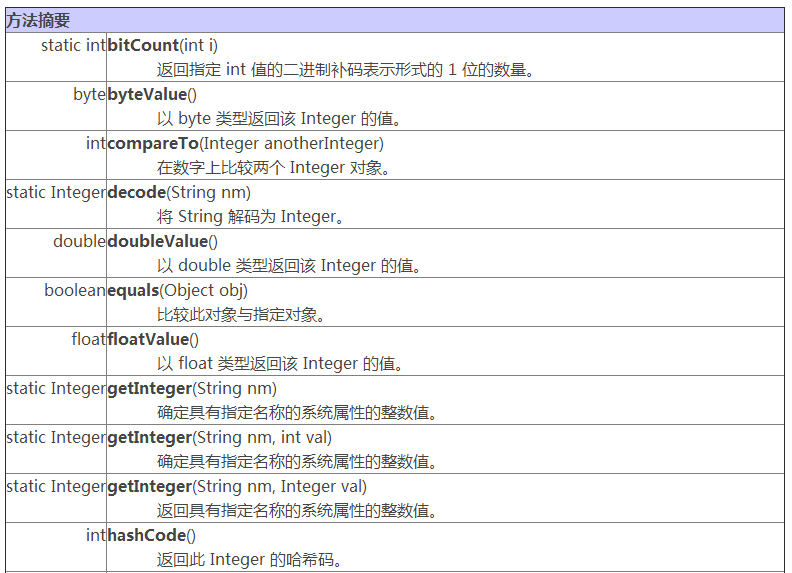
• 二者区别

  • Integer是int的包装类，int则是java的一种基本数据类型
  • Integer变量必须实例化后才能使用，而int变量不需要
  • Integer实际是对象的引用，当new一个Integer时，实际上是生成一个指针指向此对象；而int则是直接存储数据值
  • Integer的默认值是null，int的默认值是0

所以我把数组定义类型统一为Integer类型就可以了。

其他

这次实验的实验五记得是比较麻烦的一个，主要牵扯的类太多，经常出现错误要从很多之前的类里排查，会比较麻烦。但在修改过程中也学习到了新的知识。这次实验主要是关于排序和查找。也学会了更多的算法，温习了Junit的使用。

参考

• 彻底让你明白 Integer 类和 int 基本数据类型的区别
• [[Data Structure & Algorithm] 七大查找算法 ](http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching)