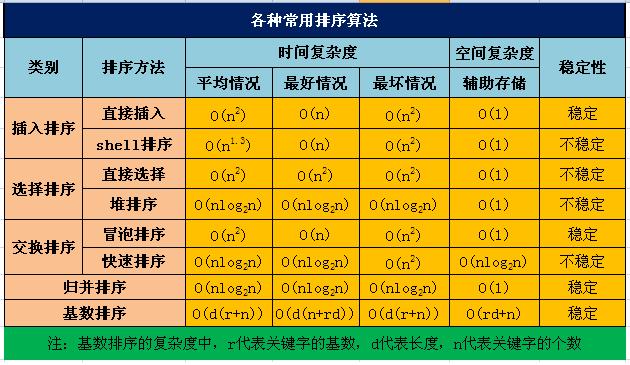
各排序的时间复杂度分析
插入排序——直接插入排序
-
在最好的情况下,序列已经是有序的,每次插入元素最多只需要与有序表中最后一个元素进行比较,时间复杂度为O(n)。在最坏的情况下,每次插入元素需要与前面所有的元素进行比较,时间复杂度为O(n2),平均时间复杂度为O(n2)。
-
代码分析
public static <T extends Comparable<T>> void insertionSort(T[] data) { //外层循环次数为n,时间复杂度为O(n) for (int index = 1; index < data.length; index++) { T key = data[index]; int position = index; //内层循环次数为n,时间复杂度为O(n) while (position > 0 && data[position-1].compareTo(key) > 0) { data[position] = data[position-1]; position--; } data[position] = key; } }
插入排序——希尔排序
-
它的基本思想是:假设序列中有n个元素,首先选择一个间隔gap,将全部的序列分为gap个子序列,然后分别在子序列内部进行简单插入排序,得到一个新的主序列;而后缩小gap,再得到子序列,对子序列进行简单插入排序,又再次得到新的主序列,直到gap=1为止。在算法中,排序前期,由于gap值比较大,插入排序的元素个数少,排序快,到了排序后期,由于前面的排序导致序列已经基本有序,插入排序对于有序的序列效率很高。所以说希尔排序最好的情况:缩小增量的插入排序,待排序已经有序。时间复杂度O(n),一般情况为下平均时间复杂度o(n1.3),最差也是时间复杂度o(n1.3)。希尔排序的时间复杂度与gap的选择有很大的关系,一般时间复杂度是低于O(n^2)。
-
需要注意的是:希尔排序的时间复杂度依赖于所取希尔序列的函数,但是到目前为止还没有一个最好的希尔序列。有人在大量的实验后得出结论:当n在某个特定的范围后希尔排序的比较和移动次数减少至n^1.3 不管增量序列如何取值,都应该满足最后一个增量值为1.
选择排序——简单选择排序
-
简单选择排序不论是否序列已经有序每个数都需要进行n-1次最小数选择,所以它的最好、最坏以及平均时间复杂度都是O(n^2)。
-
代码分析
public static <T extends Comparable<T>> void selectionSort(T[] data) { int min; T temp; //外层循环次数为n-1,时间复杂度为O(n) for (int index = 0; index < data.length-1; index++) { min = index; //内层循环次数为n,时间复杂度为O(n) for (int scan = index+1; scan < data.length; scan++) { if (data[scan].compareTo(data[min])<0) { min = scan; } } swap(data, min, index); } }
选择排序——堆排序
-
把待排序的元素按照大小在二叉树位置上排列,排序好的元素要满足:父节点的元素要大于等于其子节点;这个过程叫做堆化过程,如果根节点存放的是最大的数,则叫做大根堆;如果是最小的数,自然就叫做小根堆了。根据这个特性(大根堆根最大,小根堆根最小),就可以把根节点拿出来,然后再堆化下,再把根节点拿出来,,,,循环到最后一个节点,就排序好了。整个排序主要核心就是堆化过程,堆化过程一般是用父节点和他的孩子节点进行比较,取最大的孩子节点和其进行交换;但是要注意这应该是个逆序的,先排序好子树的顺序,然后再一步步往上,到排序根节点上。然后又相反(因为根节点也可能是很小的)的,从根节点往子树上排序。最后才能把所有元素排序好。
-
时间复杂度在任何情况下都为O(nlogn)
堆排序的时间复杂度为O(nlogn),需要一个临时空间用于交换元素,所以空间复杂度为O(1)。 -
排序包括两个阶段,初始化建堆和重建堆。所以堆排序的时间复杂度由这两方面组成。
-
初始化堆:假设高度为k,则从倒数第二层右边的节点开始,这一层的节点都要执行子节点比较然后交换(如果顺序是对的就不用交换);倒数第三层,则会选择其子节点进行比较和交换,如果没交换就可以不用再执行下去了。如果交换了,那么又要选择一支子树进行比较和交换;高层也是这样逐渐递归。
那么总的时间计算为:s = 2^( i - 1 ) * ( k - i );其中 i 表示第几层,2^( i - 1) 表示该层上有多少个元素,( k - i) 表示子树上要比较的次数。
S = 2^(k-2) * 1 + 2(k-3)2…..+2(k-2)+2(0)*(k-1) ===> 因为叶子层不用交换,所以i从 k-1 开始到 1;
S = 2^k -k -1;又因为k为完全二叉树的深度,而log(n) =k,把此式带入;
得到:S = n - log(n) -1,所以时间复杂度为:O(n) -
排序重建堆:在每次重建时,随着堆的容量的减小,层数会下降,函数时间复杂度会变化。重建堆一共需要n-1次循环,每次循环的比较次数为log(i),相加约为nlog(n)。
-
所以总的时间复杂度为O(n+nlogn)=O(nlogn)。
-
交换排序——冒泡排序
-
在最好的情况下,序列已经是有序的,只进行了第一趟冒泡比较,此时算法的时间复杂度为O(n)。在最坏的情况下,执行了n-1次冒泡,时间复杂度为O(n^2)。
-
代码分析:
public static <T extends Comparable<T>> void bubbleSort(T[] data) { int position, scan; T temp; //循环次数为n-1,时间复杂度为O(n) for (position = data.length - 1; position >= 0; position--) { //循环次数为n,时间复杂度为O(n) for (scan = 0; scan <= position - 1; scan++) { if (data[scan].compareTo(data[scan+1]) > 0) { swap(data, scan, scan + 1); } } } }
交换排序——快速排序
- 时间复杂度分析:快速排序每次要将列表分成两个分区,递归的次数取决于元素的数目,最理想的情况下,每次划分左右两部分的长度相等,需要递归次nlog2n次,平均次数也为nlog2n次,而每次分区后要进行n次比较操作,因此平均时间复杂度为O(nlogn)。快速排序比大部分排序算法都要快,但快速排序是一个非常不稳定的排序,因为若初始序列按关键码有序或基本有序时,快速排序反而蜕化为冒泡排序,此时它的时间复杂度就为O(n^2)了。
归并排序
-
归并排序是先递归的把数组划分为两个子数组,一直递归到数组中只有一个元素,然后再调用函数把两个子数组排好序,因为该函数在递归划分数组时会被压入栈,所以这个函数真正的作用是对两个有序的子数组进行排序。
-
时间复杂度分析:每次归并时要将待排序列表中的所有元素遍历一遍,因次时间复杂度为O(n)。与快速排序类似,归并排序也先将列表不断分区直至每个列表只剩余一个元素,这个过程需要进行log2n次分区。因此归并排序的平均时间复杂度为O(nlogn)。因为不管元素在什么情况下都要做这些步骤,所以花销的时间是不变的,所以该算法的最优时间复杂度和最差时间复杂度及平均时间复杂度都是一样的为:O( nlogn )。
-
复杂公式分析:总时间=分解时间+解决问题时间+合并时间。分解时间就是把一个待排序序列分解成两序列,时间为一常数,时间复杂度o(1)。解决问题时间是两个递归式,元素长度为n的归并排序所消耗的时间T[n],把一个规模为n的问题分成两个规模分别为n/2的子问题,时间为2T(n/2)。合并时间复杂度为o(n)。总时间T(n)=2T(n/2)+o(n),所以得出的结果为:T[n] = O( nlogn )。参考: http://blog.csdn.net/yuzhihui_no1/article/details/44198701#t2
基数排序
-
基本思想就是把元素从个位排好序,然后再从十位排好序,,,,一直到元素中最大数的最高位排好序,那么整个元素就排好序了。
-
时间复杂度分析:对于有n个元素的序列,对每一位数放置和收集的时间为O(n+r),则其时间复杂度为 O(d(n+r))。(r为基数,d为位数)
-
既然基数排序的时间复杂度这么低,为什么不是所有的排序都使用基数排序法呢?
首先,基数排序无法创造出一个使用于所有对象类型的泛型基数排序,因为在排序过程中要进行关键字取值的切分,因此关键字的类型必须是确定的。
其次,当基数排序中的基数大小与列表中的元素数目非常接近时,基数排序法的实际时间复杂度接近于O(n^2)。
八大排序方法分析