关于一次同余方程的一类解法（exgcd，CRT，exCRT）

1.解同余方程：

同余方程可以转化为不定方程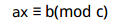，其实就是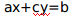，这样的问题一般用拓展欧几里德算法求解。

LL exgcd(LL a,LL b,LL &x,LL &y){
    if(!b){
        x=1;y=0;
        return a;
    }
    LL gcd=exgcd(b,a%b,x,y);
    LL t=x;
    x=y;
    y=t-a/b*x;
    return gcd;
} 

 2.解同余方程组（任意两个模意义互质）用CRT。

LL CRT(){
    LL ans=0,M=1,x,y;
    for(int i=1;i<=n;i++) M*=m[i];
    for(int i=1;i<=n;i++){
        LL Mi=M/m[i];
        exgcd(Mi,m[i],x,y);
        ans=(ans+a[i]*Mi*x)%M;
    }return (ans+M)%M;
}

3.解同余方程组（任意两个模意义不一定互质）用exCRT。

void exCRT(){
    int i=2;i<=n;i++){
        LL m1=m[i-1],m2=m[i],a1=a[i-1],a2=a[i],g=gcd(m1,m2);
        if((a2-a1)%g!=0){flag=1;break;}
        m[i]=m2/g*m1;
        a[i]=(inv(m1/g,m2/g)*(a2-a1)/g)%(m2/g)*m1+a1;
        a[i]=(a[i]%m[i]+m[i])%m[i];
    }printf("%lld
",flag?-1:a[n]);
}