zoukankan      html  css  js  c++  java

  • 【NOIP2016】天天爱跑步

    题目描述

    小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。«天天爱跑步»是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。

    这个游戏的地图可以看作一一棵包含 个结点和 条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从到的连续正整数。

    现在有个玩家,第个玩家的起点为 ,终点为  。每天打卡任务开始时,所有玩家在第秒同时从自己的起点出发, 以每秒跑一条边的速度, 不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)

    小C想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点的观察员会选择在第秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第秒也理到达了结点  。 小C想知道每个观察员会观察到多少人?

    注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点作为终点的玩家: 若他在第秒重到达终点,则在结点的观察员不能观察到该玩家;若他正好在第秒到达终点,则在结点的观察员可以观察到这个玩家。

    输入输出格式

    输入格式：

    第一行有两个整数和 。其中代表树的结点数量, 同时也是观察员的数量, 代表玩家的数量。

    接下来 行每行两个整数和 ,表示结点 到结点 有一条边。

    接下来一行 个整数,其中第个整数为 , 表示结点出现观察员的时间。

    接下来 行,每行两个整数,和,表示一个玩家的起点和终点。

    对于所有的数据,保证 。

    输出格式：

    输出1行 个整数,第个整数表示结点的观察员可以观察到多少人。

    输入输出样例

    输入样例#1：
    6 3
2 3
1 2 
1 4 
4 5 
4 6 
0 2 5 1 2 3 
1 5 
1 3 
2 6
    输出样例#1：
    2 0 0 1 1 1
    输入样例#2：
    5 3 
1 2 
2 3 
2 4 
1 5 
0 1 0 3 0 
3 1 
1 4
5 5
    输出样例#2：
    1 2 1 0 1

    说明

    【样例1说明】

    对于1号点，，故只有起点为1号点的玩家才会被观察到，所以玩家1和玩家2被观察到，共有2人被观察到。

    对于2号点，没有玩家在第2秒时在此结点，共0人被观察到。

    对于3号点，没有玩家在第5秒时在此结点，共0人被观察到。

    对于4号点，玩家1被观察到，共1人被观察到。

    对于5号点，玩家1被观察到，共1人被观察到。

    对于6号点，玩家3被观察到，共1人被观察到。

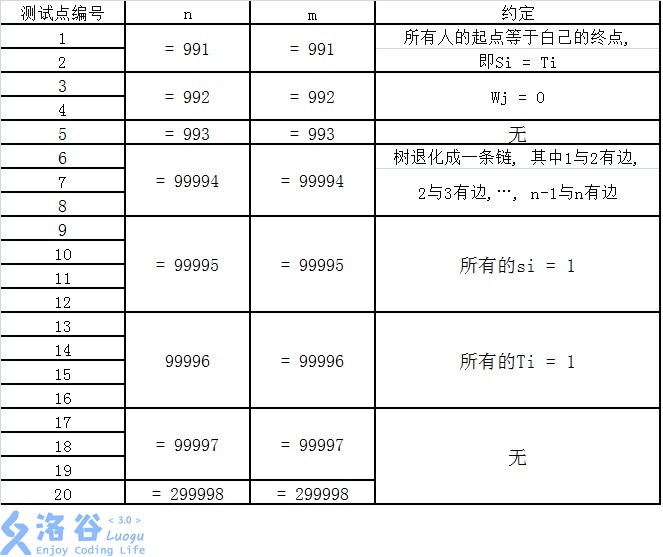
    【子任务】

    每个测试点的数据规模及特点如下表所示。 提示: 数据范围的个位上的数字可以帮助判断是哪一种数据类型。

    题解：

    这是一道比较有趣的树上统计题，并没有什么高级算法，只是思想巧妙：

    用的大概是一种差分思想，是用桶实现的.（即t[i]表示深度为i的点的个数）

    我们要将跑的过程转化成 计算对一个点有贡献的路径的个数

    于是我们可以开始讨论.

    我们先看一条路径s-t：

    1.先是从下往上（s-lca）跑，如果对一个点i有贡献仅当deep[i]+w[i]=deep[s]时.

       且对于每一个点，deep[i]+w[i]是定值.所以我们把所有路径的S打上标记，

       然后按照dfs序遍历，如果一个点x有标记就把t[deep[x]]+=mark[x].

       然后每一个点都做同样的操作：ans[x]+=t[deep[i]+w[i]].

    2.然后是lca-t，如果满足L-deep[t]=w[i]-dep[i]时可产生贡献，同样在终点t打上++标记， 

       然后再回溯的回程中就会把t-lca有贡献的点都统计完 考虑到等式两边都有可能产生负数，

       于是就把数组偏移一个N,即所有的访问和标记都+N

    3.考虑到子树之间 和 子树对父节点以上节点 统计的影响 我们要在lca处打上标记，消除对父节点以上节点的影响

    然后进入下一层dfs之前要保存t[i]的值，设为pre,那么答案就为回溯以后的t[i]-pre.

    4.然后调样例的时候会发现如果lca满足统计条件会被统计两次，于是最后的时候需要减掉重复情况

      1 #include<iostream>
  2 #include<cstdio>
  3 #include<cmath>
  4 #include<cstring>
  5 #include<vector>
  6 using namespace std;
  7 const int N=319998,P=300001;
  8 int gi(){
  9     int str=0;char ch=getchar();
 10     while(ch>'9' || ch<'0')ch=getchar();
 11     while(ch>='0' && ch<='9')str=str*10+ch-'0',ch=getchar();
 12     return str;
 13 }
 14 vector<int>q1[N],q2[N],q3[N];
 15 int n,m,head[N],w[N],num=0,maxdep=0;
 16 struct Lin{
 17     int next,to;
 18 }a[N*2];
 19 int Head[N],NUM=0;
 20 struct Linn{
 21     int next,to,id;
 22 }e[N*2];
 23 struct Path{
 24     int s,t,dis,lca;
 25 }q[N];
 26 int fa[N],dep[N];bool vis[N];
 27 int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
 28 void init(int x,int y){a[++num].next=head[x];a[num].to=y;head[x]=num;a[++num].next=head[y];a[num].to=x;head[y]=num;}
 29 void init2(int x,int y,int idd){e[++NUM].next=Head[x];e[NUM].to=y;e[NUM].id=idd;Head[x]=NUM;e[++NUM].next=Head[y];e[NUM].to=x,e[NUM].id=idd;Head[y]=NUM;}
 30 void tarjan(int x,int last)
 31 {
 32     int u,v,lca;
 33     vis[x]=true;
 34     if(dep[x]>maxdep)maxdep=dep[x];
 35     for(int i=head[x];i;i=a[i].next)
 36     {
 37         u=a[i].to;
 38         if(u==last)continue;
 39         dep[u]=dep[x]+1;tarjan(u,x);fa[u]=x;
 40     }
 41     for(int i=Head[x];i;i=e[i].next)
 42     {
 43         v=e[i].to;
 44         if(vis[v])
 45         {
 46             lca=find(v);
 47             q[e[i].id].lca=lca;
 48             q[e[i].id].dis=dep[v]+dep[x]-(dep[lca]<<1);
 49         }
 50     }
 51 }
 52 int t[N],ans[N],tt[N*2],mark[N];
 53 void dfs1(int x,int last)
 54 {
 55     int u,now=dep[x]+w[x],pre=0;
 56     if(now<=maxdep)pre=t[now];
 57     for(int i=head[x];i;i=a[i].next){
 58         u=a[i].to;
 59         if(u==last)continue;
 60         dfs1(u,x);
 61     }
 62     t[dep[x]]+=mark[x];
 63     if(now<=maxdep)ans[x]+=t[now]-pre;
 64     int size=q1[x].size();
 65     for(int i=0;i<size;i++)t[q1[x][i]]--;
 66 }
 67 void dfs2(int x,int last)
 68 {
 69     int u,now=w[x]-dep[x]+P,pre=tt[now];
 70     for(int i=head[x];i;i=a[i].next){
 71         u=a[i].to;
 72         if(u==last)continue;
 73         dfs2(u,x);
 74     }
 75     int size=q2[x].size();
 76     for(int i=0;i<size;i++)tt[q2[x][i]]++;
 77     ans[x]+=tt[now]-pre;
 78     size=q3[x].size();
 79     for(int i=0;i<size;i++)tt[q3[x][i]]--;
 80 }
 81 int main()
 82 {
 83     n=gi();m=gi();
 84     int x,y;
 85     for(int i=1;i<n;i++){
 86         x=gi();y=gi();
 87         init(x,y);
 88     } 
 89     for(int i=1;i<=n;i++)w[i]=gi(),fa[i]=i;
 90     for(int i=1;i<=m;i++)
 91     {
 92         q[i].s=gi();q[i].t=gi();
 93         init2(q[i].s,q[i].t,i);
 94     }
 95     dep[1]=1;
 96     tarjan(1,1);
 97     for(int i=1;i<=m;i++)
 98     {
 99         mark[q[i].s]++;
100         q1[q[i].lca].push_back(dep[q[i].s]);
101     }
102     dfs1(1,1);
103     for(int i=1;i<=m;i++)
104     {
105         q2[q[i].t].push_back(q[i].dis-dep[q[i].t]+P);
106         q3[q[i].lca].push_back(q[i].dis-dep[q[i].t]+P);
107     }
108     dfs2(1,1);
109     for(int i=1;i<=m;i++)if(w[q[i].lca]+dep[q[i].lca]==dep[q[i].s])ans[q[i].lca]--;
110     for(int i=1;i<=n;i++)printf("%d ",ans[i]);
111     return 0;
112 }

     
  • 相关阅读:
    MySql基础-1
    ClearSilver模板编程概述_转
    ehcache memcache redis 三大缓存男高音_转
    memcached完全剖析--1. memcached的基础 _转
    小组的创建
    现代软件工程 第7-9章作业
    现代软件工程 第3~6章作业
    现代软件工程作业 第二章 Github的使用
    现代软件工程作业-- GitHub的学习
    现代软件工程作业 GitHub的学习
  • 原文地址：https://www.cnblogs.com/Yuzao/p/6918931.html
Copyright © 2011-2022 走看看