题目描述
经过千辛万苦小 A 得到了一块切糕,切糕的形状是长方体,小 A 打算拦腰将切糕切成两半分给小 B。出于美观考虑,小 A 希望切面能尽量光滑且和谐。于是她找到你,希望你能帮她找出最好的切割方案。
出于简便考虑,我们将切糕视作一个长 P、宽 Q、高 R 的长方体点阵。我们将位于第 z层中第 x 行、第 y 列上(1≤x≤P, 1≤y≤Q, 1≤z≤R)的点称为(x,y,z),它有一个非负的不和谐值 v(x,y,z)。一个合法的切面满足以下两个条件:
-
与每个纵轴(一共有 P*Q 个纵轴)有且仅有一个交点。即切面是一个函数 f(x,y),对于所有 1≤x≤P, 1≤y≤Q,我们需指定一个切割点 f(x,y),且 1≤f(x,y)≤R。
- 切面需要满足一定的光滑性要求,即相邻纵轴上的切割点不能相距太远。对于所有的 1≤x,x’≤P 和 1≤y,y’≤Q,若|x-x’|+|y-y’|=1,则|f(x,y)-f(x’,y’)| ≤D,其中 D 是给定的一个非负整数。 可能有许多切面f 满足上面的条件,小A 希望找出总的切割点上的不和谐值最小的那个。
输入输出格式
输入格式:
第一行是三个正整数P,Q,R,表示切糕的长P、 宽Q、高R。第二行有一个非负整数D,表示光滑性要求。接下来是R个P行Q列的矩阵,第z个 矩阵的第x行第y列是v(x,y,z) (1<=x<=P, 1<=y<=Q, 1<=z<=R)。 100%的数据满足P,Q,R<=40,0<=D<=R,且给出的所有的不和谐值不超过1000。
输出格式:
仅包含一个整数,表示在合法基础上最小的总不和谐值。
输入输出样例
2 2 2 1 6 1 6 1 2 6 2 6
6
说明
最佳切面的f为f(1,1)=f(2,1)=2,f(1,2)=f(2,2)=1
题解:
好题啊......这是个标准最小割模型
我们拆点,把选点改成割边
考虑如果没有限制D的话,直接对于每个位置(x,y)拆成R个点,建S->1->2->....->R连边即可 ,其实直接取min就好(-.-!)
但是如果有了对D的限制我们就要考虑对于一个位置i (i=1..R)我们如果向i-D连边便可满足D的限制,为什么?
看图:
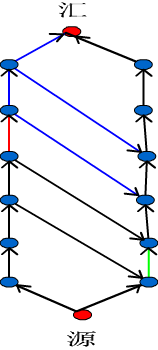
如果割了红边,那么就一定不会割到绿边上.因为S还可以通过绿边上的那条inf的边到T.所以不满足割的性质
所以可以保证不割在绿边上,那么同理从右边的i也要连向i左边的i-D (此图中没画出)
由此可以总结出最小割题目的套路:
如果一条边不能被割,我们就向它所到的点连一条inf的边 这样就依然存在到T的增广路...
1 #include <algorithm> 2 #include <iostream> 3 #include <cstdlib> 4 #include <cstring> 5 #include <cstdio> 6 #include <cmath> 7 #define id(a,b,c) (((a)-1)*41*41+((b)-1)*41+(c)) 8 using namespace std; 9 const int MS=45,N=100005,M=550000,inf=2e8; 10 int n,m,R,map[MS][MS][MS]; 11 int nxt[M],num=1,to[M],dis[M],head[N],D,S=0,T; 12 void init(int x,int y,int dist){ 13 nxt[++num]=head[x];to[num]=y;dis[num]=dist;head[x]=num; 14 } 15 void addedge(int x,int y,int dist){ 16 init(x,y,dist);init(y,x,0); 17 } 18 int q[N],dep[N]; 19 bool bfs(){ 20 int t=0,sum=1,x,u; 21 memset(dep,0,sizeof(dep)); 22 dep[S]=1;q[1]=S; 23 while(t!=sum){ 24 x=q[++t]; 25 for(int i=head[x];i;i=nxt[i]){ 26 u=to[i]; 27 if(dep[u] || dis[i]<=0)continue; 28 dep[u]=dep[x]+1;q[++sum]=u; 29 } 30 } 31 return dep[T]; 32 } 33 int dfs(int x,int flow){ 34 if(x==T || !flow)return flow; 35 int u,tmp,tot=0; 36 for(int i=head[x];i;i=nxt[i]){ 37 u=to[i]; 38 if(dep[u]!=dep[x]+1 || dis[i]<=0)continue; 39 tmp=dfs(u,min(flow,dis[i])); 40 dis[i]-=tmp;dis[i^1]+=tmp; 41 tot+=tmp;flow-=tmp; 42 if(!flow)break; 43 } 44 if(!tot)dep[x]=0; 45 return tot; 46 } 47 int maxflow(){ 48 int tot=0,tmp; 49 while(bfs()){ 50 tmp=dfs(S,inf); 51 while(tmp)tot+=tmp,tmp=dfs(S,inf); 52 } 53 return tot; 54 } 55 void work() 56 { 57 scanf("%d%d%d%d",&n,&m,&R,&D); 58 T=N-1; 59 for(int i=1;i<=R;i++){ 60 for(int j=1;j<=n;j++) 61 for(int k=1;k<=m;k++){ 62 scanf("%d",&map[j][k][i]); 63 addedge(id(j,k,i),id(j,k,i+1),map[j][k][i]); 64 } 65 } 66 for(int j=1;j<=n;j++) 67 for(int k=1;k<=m;k++){ 68 addedge(S,id(j,k,1),inf); 69 for(int i=D+1;i<=R;i++){ 70 if(j>1)addedge(id(j,k,i),id(j-1,k,i-D),inf); 71 if(k>1)addedge(id(j,k,i),id(j,k-1,i-D),inf); 72 if(j<n)addedge(id(j,k,i),id(j+1,k,i-D),inf); 73 if(k<m)addedge(id(j,k,i),id(j,k+1,i-D),inf); 74 } 75 addedge(id(j,k,R+1),T,inf); 76 } 77 printf("%d ",maxflow()); 78 } 79 80 int main() 81 { 82 work(); 83 return 0; 84 } 85